残雪
题意
是否存在一个由 \(n\) 个 \(0\) 和 \(m\) 个 \(1\) 组成的串,满足任意一个长度为 \([2L,2R]\) 的子串中 \(n\) 和 \(m\) 的个数不相等。
转化
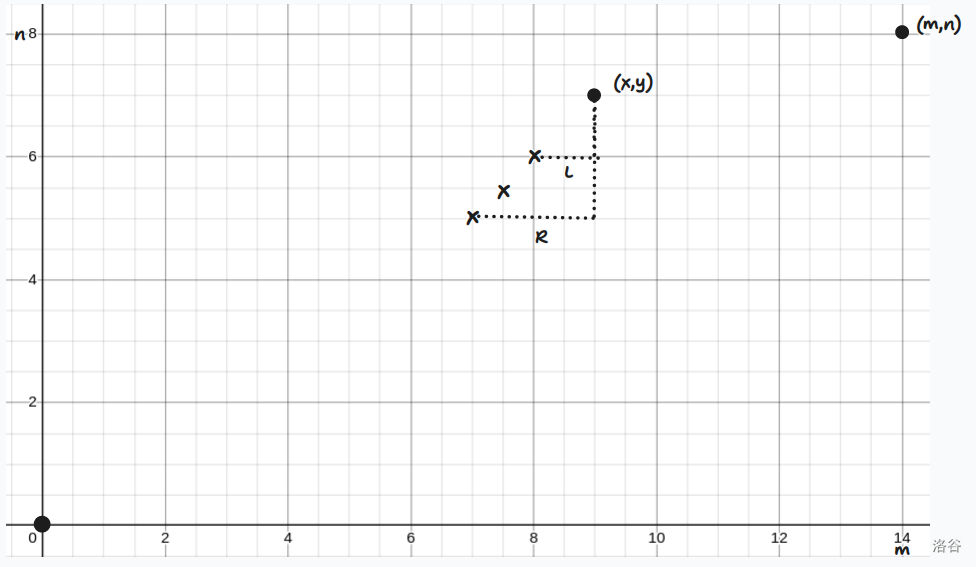
对于 01 串个数相等的问题,容易想到将其转化为在二维平面中走网格的问题,即每选择一个 \(1\) 相当于向下走一格,选择一个 \(0\) 相当于向左走一格。
这样的话,一个子串内 \(0\) 和 \(1\) 的个数相同可以表示为同时选择了 \((x,y)\) 和 \((x-k,y-k)\) 两个点,\(k\) 表示区间长度。
我们就成功将题意转化成了:从 \((m,n)\) 向左或向下走,走到 \((0,0)\),每走过一个点会产生几个不可走的位置,问是否存在一条路径,使其不经过不可走位置。
贪心
然后你发现就做完了。
这个问题看起来就很可做,我们先考虑最优的走法是什么?
显然最开始在 \((n,m)\) 的时候,会在斜下方有 \(R-L\) 个点不可走,这些不可走的点和当前走到的位置的相对位置是固定的,也就是我们怎么移动当前点,那一串不可走的位置就会跟着平移。
草率的想一下,如果某一时刻我们走到了 \((x,y)\),最近的不可走点 \((x-L,y-L)\) 已经在数轴下面了(某一维小于零),那我们就可以任意走了。所以不如让 \(n\) 作为较小的,然后钦定一开始向下走(方便下面说)。
延续上面的思路,我们尽量让不可走位置先进入数轴下面,直接贪心。先走到 \((m-L-1,n-L+1)\),然后贴着不可走位置走。最后能走到就能,不能就不能。
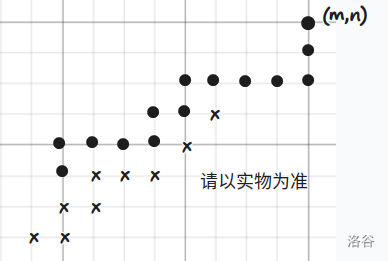
建议考虑不可走位置的边界(挨着圆点的小叉),如果最后与 x 轴的交点大于零,那就可以。
发现不可走位置会跟着路径平移,也就是不可走位置的边界会复制我们走的路径,路径又需要贴着边界走,就是一个类似螺旋升天分形的过程。建议从 \(L=R\) 的情况开始考虑,这时只有一个点,容易发现边界是有规律的,即每向下 \(L-1\) 步,向左 \(L+1\) 步为一个周期,然后你就会做了。
推广到 \(R = L+1\) 的情况,发现就是在 \(R = L\) 的边界上多了几个凸点,周期和步长不变。考虑 \(R-L\) 会对边界有什么影响。第一次会在一条笔直向下的边界上多 \(R-L\) 个凸点,由于是类似分形的结构,后面每一个周期都会多 \(R-L\) 个凸点,直到边界变成阶梯状。
现在你闭着眼都知道边界是什么样的了,计算周期,小心处理最后接近 x 轴的一小段,你就做完了。
注意一些 Corner case。
附上打表器。
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 2e4+5;
LL n,m,l,r;
char a[N][N];
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
int T; scanf("%d",&T);
while(T--)
{
scanf("%lld%lld%lld%lld",&l,&r,&n,&m);
if(n>m) swap(n,m);
for(int i=0;i<=n;i++)
for(int j=0;j<=m;j++) a[i][j]='c';
// if(n==0||m==0) puts("Yes");
queue<pair<LL,LL> > q;
q.push({n,m});
while(!q.empty())
{
LL x=q.front().first,y=q.front().second; q.pop();
a[x][y]='a';
for(int i=l;i<=r;i++)
{
if(x-i<0||y-i<0) break;
a[x-i][y-i]='b';
}
if(x-1>=0&&a[x-1][y]!='b'&&(!(y>=m-l&&x==n-l+1))) q.push({x-1,y});
else if(y-1>=0&&a[x][y-1]!='b') q.push({x,y-1});
}
if(a[0][0]=='a') puts("Yes");
else puts("No");
for(int i=n;i>=0;i--)
{
for(int j=0;j<=m;j++) printf("%c ",a[i][j]); putchar('\n');
}
putchar('\n');
}
return 0;
}



