2024.？.？？ 模拟赛 ？？？
monis
精神状态lianghao
T?
树上小模拟，赛时齌。
细节较多啊。
注意特判起始点在链的上方的情况。
多分套几次就过了。
code
#include<bits/stdc++.h>
using namespace std;
#define mi(x,y) (dfn[x]<dfn[y]?x:y)
const int N = 4e5+5;
int head[N],tot,n,m,lg[N];
struct E {int u,v;} e[N<<1];
inline void add(int u,int v) {e[++tot]={head[u],v}; head[u]=tot;}
int dfn[N],num,st[30][N],out[N],rk[N],d[N],fa[30][N];
bool fl;
inline void dfs(int u,int f)
{
dfn[u]=++num; st[0][num]=f; fa[0][u]=f;
for(int j=1;j<=27;j++) fa[j][u]=fa[j-1][fa[j-1][u]];
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v; if(v==f) continue;
d[v]=d[u]+1; dfs(v,u);
}
out[u]=num;
}
inline int get(int x,int y)
{
if(x==y) return x;
if((x=dfn[x])>(y=dfn[y])) swap(x,y); x++;
int k=lg[y-x+1];
return mi(st[k][x],st[k][y-(1<<k)+1]);
}
inline int dis(int x,int y)
{
return d[x]+d[y]-(d[get(x,y)]<<1);
}
inline int walk(int x,int y,int p)
{
if(p<=d[x]-d[get(x,y)])
{
for(int i=27;i>=0;i--) if((p>>i)&1) x=fa[i][x];
return x;
}
else
{
int t=dis(x,y);
t-=p; t=max(t,0);
int tmp=y;
for(int i=27;i>=0;i--) if((t>>i)&1) tmp=fa[i][tmp];
return tmp;
}
}
int main()
{
freopen("chase.in","r",stdin);
freopen("chase.out","w",stdout);
scanf("%d%d",&n,&m);lg[0]=-1;
for(int i=1;i<=n;i++) lg[i]=lg[i>>1]+1;
for(int i=1;i<n;i++)
{
int x,y; scanf("%d%d",&x,&y);
add(x,y); add(y,x);
}
dfs(1,0);
for(int i=1;i<=27;i++)
for(int j=1;j+(1<<i)-1<=n;j++)
st[i][j]=mi(st[i-1][j],st[i-1][j+(1<<(i-1))]);
while(m--)
{
int x,y,z; scanf("%d%d%d",&x,&y,&z);
int xx=x,yy=y,zz=z;
int l=get(x,y),l1=get(x,z),l2=get(y,z);
if(l1==l2&&l1==z) l1=l2=l;
if((l1==z&&l2==l)||(l2==z&&l1==l))
{
int time=(dis(x,z)-1)/2+1; if(x==z) time=0;
x=walk(x,y,time);
printf("%d %d\n",time,x);
}
else if(l1==l2)
{
int p=dis(z,l);
if(p>dis(x,l))
{
printf("%d %d\n",dis(z,y),y);
}
else
{
int time=(dis(x,z)-1)/2+1; if(x==z) time=0;
x=walk(x,y,time);
printf("%d %d\n",time,x);
}
}
else
{
int tmp;
if(abs(d[l1]-d[z])<abs(d[l2]-d[z])) tmp=l1;
else tmp=l2;
int p=d[z]-d[tmp];
if(p>dis(x,tmp))
{
printf("%d %d\n",dis(z,y),y);
}
else
{
x=walk(x,y,p); z=tmp;
int time=(dis(x,z)-1)/2+1; if(x==z) time=0;
x=walk(x,y,time);
printf("%d %d\n",time+p,x);
}
}
}
return 0;
}
T？
发现和出现次数有关，直接搞前缀出现次数。
发现区间出现次数就是前缀出现次数做差，直接搞差。
发现只需要 \(m\) 种数的差一样就行，所以人类智慧不关心 \(1\) 的差，只记录 \(m\) 个数的差分数组。
发现只要出现次数的差分数组相同就合法，直接上 hash。
发现每次只会改变一个数的出现次数，复杂度正确。
发现 \(\mathbb{T}\) 了，手写 hash。
code
#include<bits/stdc++.h>
using namespace std;
#define ULL unsigned long long
#define LL long long
const int N = 1e6+5,B = 919,mod = 1e6+721;
int n,m,a[N],T;
LL ans;
ULL p[N];
struct HT
{
int tot,head[mod+5];
struct node{int u,v; ULL k;} e[N];
inline void clear() {memset(head,0,sizeof(head)); tot=0;}
inline int &operator [] (const ULL k)
{
int tmp=k%mod;
for(int i=head[tmp];i;i=e[i].u)
if(e[i].k==k) return e[i].v;
e[++tot]={head[tmp],0,k}; head[tmp]=tot;
return e[tot].v;
}
} mp;
int main()
{
freopen("st.in","r",stdin);
freopen("st.out","w",stdout);
scanf("%d",&T); p[0]=1;
for(int i=1;i<N;i++) p[i]=p[i-1]*B;
while(T--)
{
mp.clear(); ans=0;
scanf("%d%d",&n,&m);
mp[0]++; ULL tmp=0;
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
if(a[i]!=1) tmp+=p[m-a[i]];
tmp-=p[m-a[i]-1];
ans+=mp[tmp];
mp[tmp]++;
}
printf("%lld\n",ans);
}
return 0;
}
T?？？
直接贪心有 \(96pts\)。
正解是 dp。
拜拜。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 5e3+5;
int n,k,top,top1;
struct L {int l,r;} line[N],st[N],let[N];
LL f[N],s[N],ans;
int main()
{
freopen("se.in","r",stdin);
freopen("se.out","w",stdout);
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++) scanf("%d%d",&line[i].l,&line[i].r);
sort(line+1,line+1+n,[&](const L &x,const L &y){return x.r-x.l>y.r-y.l;});
for(int i=1;i<=k-1;i++) ans+=line[i].r-line[i].l;
int l=0,r=1e9;
for(int i=k;i<=n;i++) l=max(l,line[i].l),r=min(r,line[i].r);
ans+=max(0,r-l);
sort(line+1,line+1+n,[&](const L &x,const L &y){return x.l<y.l;});
priority_queue<pair<int,int> > q;
for(int i=1;i<=n;i++)
{
while(!q.empty()&&q.top().first>=line[i].r) let[++top1]=line[q.top().second],q.pop();
q.push({line[i].r,i});
}
while(!q.empty()) st[++top]=line[q.top().second],q.pop();
sort(st+1,st+1+top,[&](const L &x,const L &y) {return x.l==y.l?(x.r<y.r):(x.l<y.l);});
memset(s,-0x3f,sizeof(s)); f[0]=0; s[0]=st[1].r;
for(int i=1;i<=top;i++)
{
for(int j=k;j>=1;j--)
{
f[j]=s[j-1]-st[i].l;
s[j]=max(s[j],f[j]+st[i+1].r);
}
}
for(int j=1;j<=top1;j++)
{
for(int i=k;i>1;i--)
{
f[i]=max(f[i],f[i-1]+let[j].r-let[j].l);
}
}
ans=max(ans,f[k]);
printf("%lld\n",ans);
return 0;
}
?？T?
发现这是命运。
然后开始睡觉。
？T？？!
签没签，\(\frac{i}{j}\)，直接枚举 \(j\)，\([kj,kj+0.5j)\) 都是合法的。
差分做完了。注意边界，向上取整。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 3e6+5;
int n,ans[N];
inline void write(int x) {return x?(write(x/10),putchar((x%10)|48)),void(0):(void(0));}
int main()
{
freopen("count.in","r",stdin);
freopen("count.out","w",stdout);
scanf("%d",&n);
for(int j=1;j<=n;j++)
{
for(int k=0;k*j<=n;k++)
{
ans[k*j]++; ans[k*j+((j-1)/2)+1]--;//注意
}
}
for(int i=0,sum=0;i<=n;i++)
{
sum+=ans[i];
if(i) write(sum),putchar(' ');
}
return 0;
}
T
奇奇妙妙睡大觉。
因为放右边更优，所以放左边更优。一开 是吧所有 \(&\) 放左面。算出最大答案。
后面所有贡献安慰考虑。
先选一个小可爱往最右放，这时右边一坨 or 的贡献一定位能提供，不需要前面干。
所以前面只需要除去这些贡献干就行了。变成子问题。
注意 \(ans\) 不一直是最大贡献，可能在之前处理子问题被削掉了，
后面 \(|\) 的贡献不易定和前面重，所以注意。
trick:按位与和按位或可以看成按位 min、max,可以用 ST 表维护。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+5;
#define LL long long
int n,k,m,lg[N],p[N],cnt;
LL a[N],sta[21][N],sto[21][N];
inline LL geta(int l,int r)
{
int k=lg[r-l+1];
return sta[k][l]&sta[k][r-(1<<k)+1];
}
inline LL geto(int l,int r)
{
if(l>r) return 0;
int k=lg[r-l+1];
return sto[k][l]|sto[k][r-(1<<k)+1];
}
inline LL cal(int i,int now)
{
return (((geta(1,i+1)|geto(i+2,now))&a[now+1])|geto(now+2,n));
}
int main()
{
freopen("bitop.in","r",stdin);
freopen("bitop.out","w",stdout);
scanf("%d%d",&n,&k); m=n-1-k; lg[0]=-1;
for(int i=1;i<=n;i++) lg[i]=lg[i>>1]+1;
for(int i=1;i<=n;i++) scanf("%lld",&a[i]),sta[0][i]=sto[0][i]=a[i];
for(int i=1;i<=20;i++)
for(int j=1;j+(1<<i)-1<=n;j++)
sta[i][j]=(sta[i-1][j]&sta[i-1][j+(1<<i-1)]),
sto[i][j]=(sto[i-1][j]|sto[i-1][j+(1<<i-1)]);
LL ans=(geta(1,k+1)|geto(k+2,n));
int now=n-1;
for(int i=k-1;i>=0;i--)
{
while((ans&cal(i,now))!=ans) now--;
p[++cnt]=now;
ans^=ans&geto(now+2,n);//注意
n=now; now=n-1;
}
for(int i=k;i>=1;i--) printf("%d ",p[i]);
return 0;
}
lllT
睡醒了。
又睡着了。 呼呼呼。。。
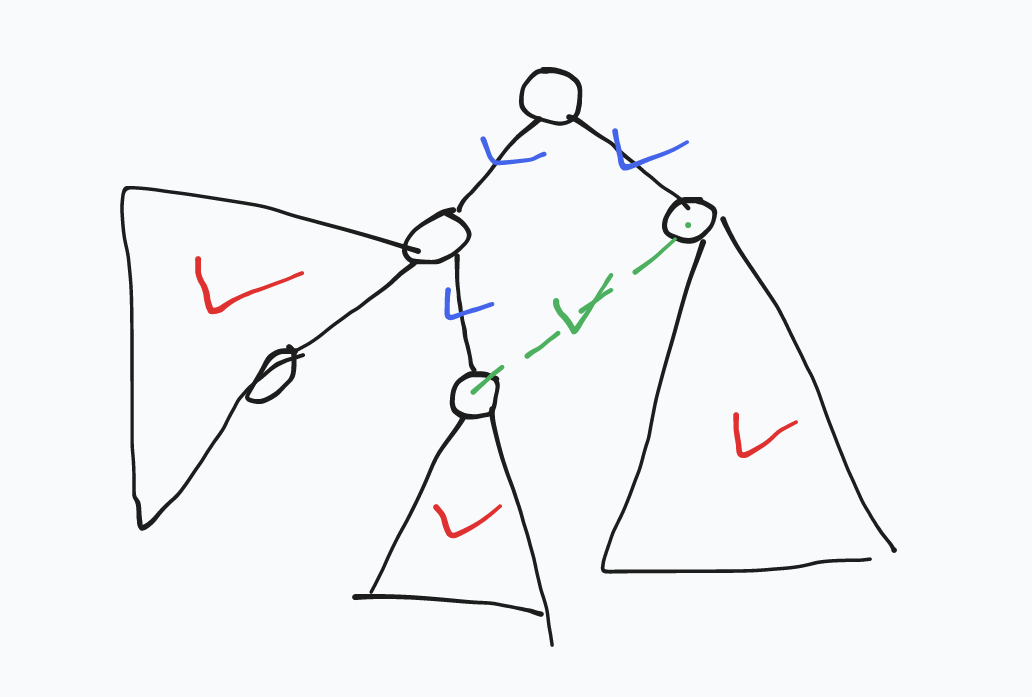
转化题意，求每一条边被走了多少次。
容易处理不加边的情况，考虑加一条边会增加哪些贡献。
-
新成环上的边。
-
环之外的子树内的边。
这些路径一定都经过新加边。
分别考虑：
1.新子树内的边
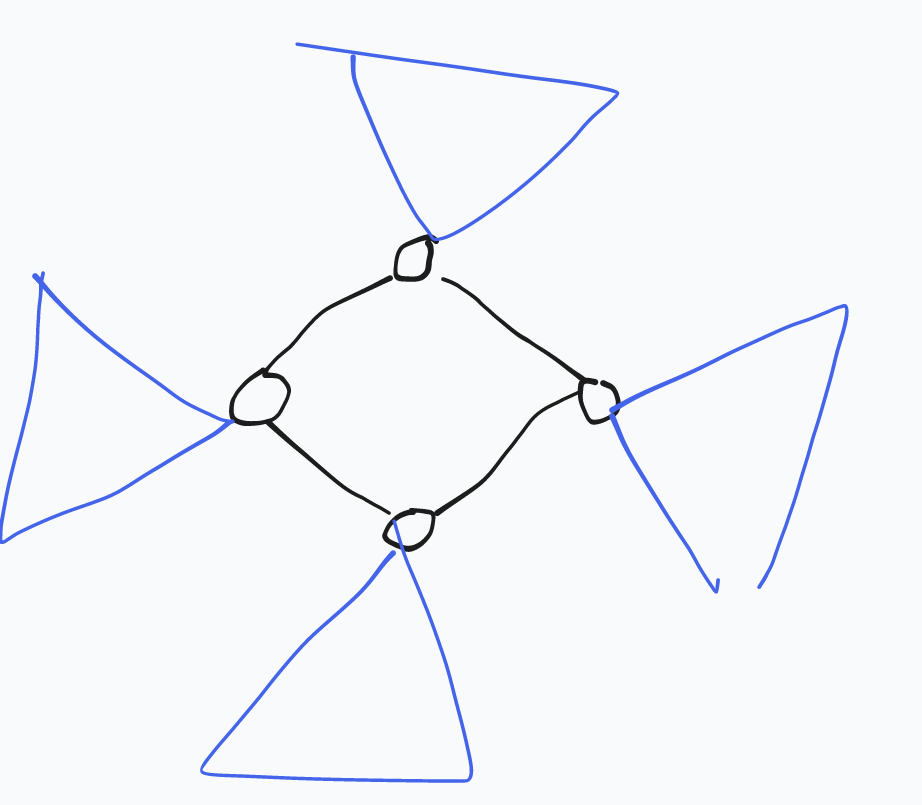
首先找出环之外的子树，子树内每一条边都可以通过新加边走到子树外另一个点，且道路唯一。
把边问题转化为点问题，每一个点要走出子树，要经过 \(dis(rt,u)\) 条子树内的边，也就是 \(dep_u-dep_{rt}\)，
假如这棵子树的大小是 \(siz\)（注意不是原子树大小，而是环上子树），子树内所有点到子树根的距离和是 \(f_u\)，
那么这一棵子树的贡献就是 \(g_u=f_u*siz\)，我们要求的 \(\sum_{u\in cir} g_u\)，
注意到两点的 \(lca\) 并不好处理，所以预处理出一个点到所有点的距离和（换根 dp）,然后可以算出 \(lca\) 的 \(g_u\)，
倍增，每个点维护不算自己这棵子树，父亲的贡献，然后跳的时候特殊处理起点和 \(lca\) 的贡献。
2.环上的边
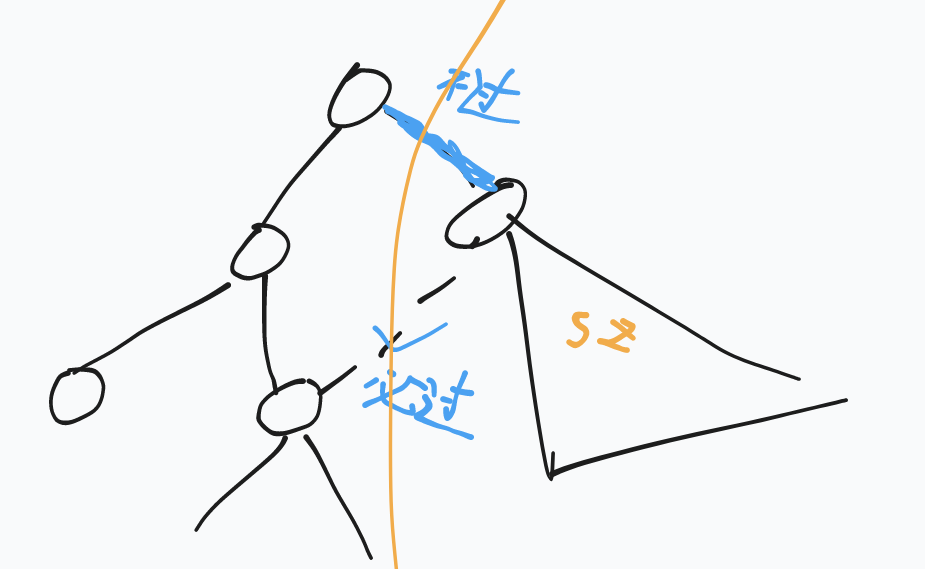
对于每一条边讨论，容斥算出一定经过环上边的路径数 \(\binom{n}{2}-\sum\binom{sz}{2}\)（所有路径减去只在环上子树内的路径，剩下的一定过环）。
然后对于每一条边，减去不经过它的次数 \(\binom{n}{2}-\sum\binom{sz}{2}-g_u\)，既然不经过它并且一定经过新加边，就相当于把图分成两部分，发现就是 \(g_u=(n-sz)sz\)（如图）,
对于环上所有边做一次，就是 \((dis+1)\binom{n}{2}-(dis+1)\sum\binom{sz}{2}-\sum g_u\)（dis 表示环的长度）。
都用类似上面倍增的方法求就行。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
#define A(x) (x>=mod?(x-mod):x)
#define mi(x,y) (dfn[x]<dfn[y]?(x):(y))
const int N = 3e5+5,mod = 998244353;
int n,q,m,ty,ans,sum;
int head[N],tot,lg[N];
struct E {int u,v;} e[N<<1];
inline void add(int u,int v) {e[++tot]={head[u],v}; head[u]=tot;}
int fa[21][N],dep[N],sz[N],st[21][N],tf[N],dfn[N],num,f[N],f1[N],g1[21][N],g2[21][N],g[21][N];
inline void dfs(int u,int faa)
{
sz[u]=1; fa[0][u]=faa; dfn[u]=++num; st[0][num]=faa; dep[u]=dep[faa]+1; f1[u]=dep[u]; f[u]=dep[u];
for(int i=1;i<=20;i++) fa[i][u]=fa[i-1][fa[i-1][u]];
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v;
if(v==faa) continue;
dfs(v,u); sum=(sum+1ll*sz[v]*(n-sz[v]))%mod; sz[u]+=sz[v];
f[u]=A(f[u]+f1[v]); f1[u]=A(f1[u]+f1[v]);
}
f[u]=(f[u]-1ll*sz[u]*dep[u]%mod+mod)%mod;
}
inline void dp(int u,int fa)
{
if(u!=1) tf[u]=(1ll*tf[fa]+n-2*sz[u]+mod)%mod;
else tf[u]=f[u];
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v; if(v==fa) continue;
dp(v,u);
}
}
inline int lca(int x,int y)
{
if(x==y) return x;
if((x=dfn[x])>(y=dfn[y])) swap(x,y);x++;
int k=lg[y-x+1];
return mi(st[k][x],st[k][y-(1<<k)+1]);
}
inline int dis(int x,int y)
{
return dep[x]+dep[y]-(dep[lca(x,y)]<<1);
}
inline int sbt(int x,int y)
{
int l=lca(x,y);
int res=((x!=l)*(1ll*f[x])*(n-sz[x])%mod+(y!=l)*(1ll*f[y])*(n-sz[y])%mod)%mod;
for(int i=20;i>=0;i--)
if(dep[fa[i][x]]>dep[l])
res=A(res+g1[i][x]), x=fa[i][x];
for(int i=20;i>=0;i--)
if(dep[fa[i][y]]>dep[l])
res=A(res+g1[i][y]),y=fa[i][y];
int siz=n-sz[x]*(x!=l)-sz[y]*(y!=l);
if(res<0) while(1);
res=(res+((1ll*tf[l]-(1ll*f[x]+sz[x])*(x!=l)%mod-(1ll*f[y]+sz[y])*(y!=l)%mod)%mod+mod)%mod*(n-siz))%mod;
return res;
}
inline int GGrun(int x,int y)
{
int l=lca(x,y),res=0;
for(int i=20;i>=0;i--)
if(dep[fa[i][x]]>=dep[l])
res=A(res+g[i][x]), x=fa[i][x];
for(int i=20;i>=0;i--)
if(dep[fa[i][y]]>=dep[l])
res=A(res+g[i][y]),y=fa[i][y];
return res;
}
inline int mhy(int x,int y)
{
int l=lca(x,y);
int res=((1ll*(x!=l)*sz[x]*(sz[x]-1)/2)%mod+(1ll*(y!=l)*sz[y]*(sz[y]-1)/2)%mod);
for(int i=20;i>=0;i--)
if(dep[fa[i][x]]>dep[l])
res=A(res+g2[i][x]), x=fa[i][x];
for(int i=20;i>=0;i--)
if(dep[fa[i][y]]>dep[l])
res=A(res+g2[i][y]),y=fa[i][y];
int siz=n-(x!=l)*sz[x]-(y!=l)*sz[y];
res=(res+(1ll*siz-1)*(siz)/2)%mod;
return res;
}
int main()
{
freopen("tree.in","r",stdin);
freopen("tree.out","w",stdout);
scanf("%d%d%d",&n,&q,&ty); lg[0]=-1;
for(int i=1;i<=n;i++) lg[i]=lg[i>>1]+1;
for(int i=1;i<n;i++)
{
int x,y; scanf("%d%d",&x,&y);
add(x,y); add(y,x);
}
dfs(1,0); dp(1,0);
for(int i=2;i<=n;i++)
{
int siz=sz[fa[0][i]]-sz[i];
g1[0][i]=((1ll*f[fa[0][i]]-f[i]-sz[i])%mod+mod)*(n-siz)%mod;
g2[0][i]=(1ll*siz*(siz-1)/2)%mod;
g[0][i]=(1ll*sz[i])*(n-sz[i])%mod;
}
for(int i=1;i<=20;i++)
for(int j=1;j+(1<<i)-1<=n;j++)
st[i][j]=mi(st[i-1][j],st[i-1][j+(1<<(i-1))]);
for(int i=1;i<=20;i++)
{
for(int j=1;j<=n;j++)
{
g1[i][j]=A(g1[i-1][j]+g1[i-1][fa[i-1][j]]);
g2[i][j]=A(g2[i-1][j]+g2[i-1][fa[i-1][j]]);
g[i][j]=A(g[i-1][j]+g[i-1][fa[i-1][j]]);
}
}
while(q--)
{
int x,y; scanf("%d%d",&x,&y);
x^=ans*ty; y^=ans*ty;
if(x==y) ans=sum;
else
{
int D=(dis(x,y)+1)%mod;
ans=(sum+(1ll*n*(n-1)/2)%mod*D%mod)%mod;
ans=(1ll*ans+sbt(x,y)+mod)%mod;
ans=(ans-1ll*mhy(x,y)*D%mod+mod)%mod;
ans=(ans-GGrun(x,y)%mod+mod)%mod;
}
printf("%d\n",(ans));
}
return 0;
}
ajdlskfjjjl T
dp，考虑每一个加号会结算一次，所以维护上一个加号前所有表达式的答案，上一个加号之后连乘的答案，和最后一个乘号前面的连乘。
这样加和乘操作很好理解，如果加入一个数，那么连乘的一坨会乘十，新加入的数的贡献次数按最后一个乘号前面的连乘系数确定。
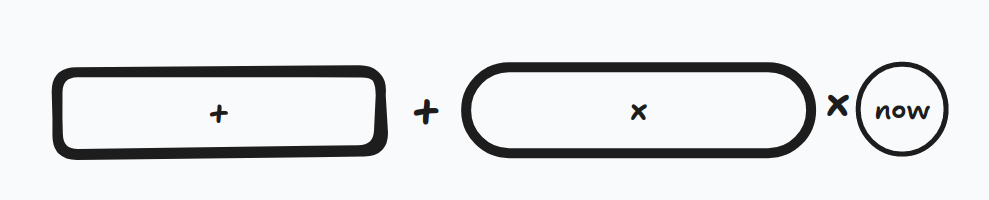
注意加入一个数时，它自己的贡献还与从起点到它的路径数有关，而不只是一次贡献。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 2e3+5,mod = 998244353;
#define A(x) (x>mod?(x-mod):(x))
int n,m;
char s[N][N];
int f[N][N],g[N][N],y[N][N],h[N][N];
int main()
{
freopen("grid.in","r",stdin);
freopen("grid.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%s",s[i]+1);
f[1][1]=0; h[1][1]=g[1][1]=1; y[1][1]=s[1][1]-'0';
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(i==1&&j==1) continue;
f[i][j]=A(f[i-1][j]+f[i][j-1]);
g[i][j]=A(g[i-1][j]+g[i][j-1]);
y[i][j]=A(y[i-1][j]+y[i][j-1]);
h[i][j]=A(h[i-1][j]+h[i][j-1]);
if(s[i][j]=='+')
{
f[i][j]=A(f[i][j]+y[i][j]);
g[i][j]=h[i][j]; y[i][j]=0;
}
else if(s[i][j]=='*')
{
g[i][j]=y[i][j]; y[i][j]=0;
}
else
{
y[i][j]=(10ll*y[i][j]+1ll*g[i][j]*(s[i][j]^48))%mod;
}
}
}
printf("%d\n",A(f[n][m]+y[n][m]));
return 0;
}
T5
根号分治好题。
据说由于点比较稀疏所以想到根号分治？
首先按列分组，问题变为求两组的交。
按组大小分，分为 \(\ge S\) 和 \(\lt S\) 两类。
-
\(\ge S\)：最多有 \(\frac{n}{S}\) 组，对于每一组记录那些位置出现过，然后遍历其他的所有组，复杂度 \(O(\frac{n^2}{S})\)，这就处理完了 \(\ge S\) 和其他的所有之间的贡献。
-
\(\lt S\)：不太好想，注意到每一组只会有 \(S\) 个，记住一共只有 \(n\) 个点，而不是 \(nS\) 个，
自然想到按值域，对于每一位开
vector记录有哪些组存在这一位。注意这里每一个点只会加入一组，一共只有 \(n\) 个点，时空都是 \(O(n)\) 的。
然后遍历值域，这时只关心包含它的组，这相当于固定下界，只要上界相同就行了，开桶记所有可能上界的出现次数，注意这里要小心维护，一不小心就爆 \(O(n^2)\)。
分析复杂度：每一组的大小只有 \(S\)，每一个点只会在下界在同一组的它的下方的时候被遍历到，所以每个点只会被遍历 \(S\) 次，复杂度 \(O(nS)\)。
取 \(S=\sqrt{n}\)，做完了。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 2e5+5;
int n,tl[N],tot,S,cc[N],ys[N];
struct node {int x,y;} a[N];
vector<int> s[N];
vector<int > l,r,z[N];
unordered_map<int,int> mp;
LL ans;
bool vs[N];
int main()
{
freopen("rect.in","r",stdin);
freopen("rect.out","w",stdout);
scanf("%d",&n); S=sqrt(n);
for(int i=1;i<=n;i++) scanf("%d%d",&a[i].x,&a[i].y),tl[++tot]=a[i].x;
sort(tl+1,tl+1+tot);
tot=unique(tl+1,tl+1+tot)-tl-1;
for(int i=1;i<=tot;i++) mp[tl[i]]=i;
for(int i=1;i<=n;i++) a[i].x=mp[a[i].x],s[a[i].x].push_back(a[i].y);
for(int i=1;i<=tot;i++)
{
sort(s[i].begin(),s[i].end());
if(s[i].size()>=S) l.push_back(i);
else r.push_back(i);
}
int sz1=l.size(),sz2=r.size();
for(int i=0;i<sz1;i++)
{
for(int j:s[l[i]]) vs[j]=1;
for(int j=i+1;j<sz1;j++) if(i!=j)
{
int cnt=0;
for(int k:s[l[j]]) if(vs[k]) cnt++;
ans+=(1ll*cnt)*(cnt-1)/2;
}
for(int j=0;j<sz2;j++)
{
int cnt=0;
for(int k:s[r[j]]) if(vs[k]) cnt++;
ans+=(1ll*cnt)*(cnt-1)/2;
}
for(int j:s[l[i]]) vs[j]=0;
}
for(int i=0;i<sz2;i++)
for(int j:s[r[i]])
z[j].push_back(r[i]);
for(int i=1;i<=n;i++)
{
int ccc=0;
for(int j:z[i])
{
int sz=s[j].size();
for(int k=sz-1;k>=0;k--)
{
if(s[j][k]<=i) break;
if(!cc[s[j][k]]) ys[++ccc]=s[j][k];
cc[s[j][k]]++;
}
}
for(int k=1;k<=ccc;k++) ans+=1ll*cc[ys[k]]*(cc[ys[k]]-1)/2,cc[ys[k]]=0;
}
printf("%lld\n",ans);
return 0;
}
T GGrun
真睡醒了。
dp 优化好题。
首先放结论：
-
如果某一个水杯向前倒了，那么后面所有的水杯一定都没水。
-
某一个水杯有 \(k\) 的水，向前倒，只会倒 \(min(k,a_j)\) 个水。而不会因为前面的水杯里本来有水，倒满了，导致自己剩下。
结论一不太好想，但是很好证，每一个水杯只能使后面一个水杯有水，能进行转移的水杯一定有水，所以水会像一条链一样跳跃，而不会分叉。
结论二是结论一的推论，当前进行转移的水一定是从之前的水杯倒过来的，也就是之前的水杯里的水的一部分，所以如果向前倒的水杯里没水，那么就是 \(min(k,a_j)\)，否则就是 \(k\)。
然后朴素 \(O(n^3)\)，设计状态 \(f_{i,j}\) 表示第 \(i\) 个水杯里有 \(j\) 个水的概率。
转移比较朴素，方法较多，不再赘述。
考虑运用刚才的结论。既然每次向前转移都会使进程结束，也就是后面不会再有状态，所以不妨在向前倒的情况直接统计答案。
如果倒完当前杯里剩了水，那这部分水也不会再被倒走，也可以直接统计答案。
发现这样转化虽然对复杂度没有影响，但是我们将其中两部分更新答案的操作从状态转移中抽出来了。
不管 \(f\) 数组的转移，先考虑抽出来的更新答案的两部分。
发现有 \(min\) 操作，容易想到分讨。然后你发现可以对 \(f\) 数组维护前缀和，这样可以在 \(O(n^2)\) 内解决更新答案。
回过头考虑状态转移，\(\forall j>i,f_{j,min(k,a_j)} \gets f_{j,min(k,a_j)}+\frac{f_{i,k}}{n-1}\)，
发现这是一个刷表的形式（已知当前，更新后面），不好维护，把它转化成填表的形式（已知前面，更新当前）。
有注意力的小盆友早就发现这就是二维前缀和了，画图比较好考虑，\(f_{i,a_i}\) 就是倒满的情况，前面所有比它水多的都能更新它，表现在图上就是一个矩形。剩下的情况就是由之前等水量的所有的状态转移过来，就是一个一维前缀和。
所以维护前缀和，你发现你会 \(O(n^2)\) 了。
简单将前缀和数组维护在线段树上，这样你发现每次可以通过一系列操作由前缀和数组转化为 \(f\) 数组（维护信息及操作方法不唯一），这就解决了 \(f\) 的更新问题。
之后考虑更新答案。首先是给别人倒水，自己剩下的。这部分就是 \(f_{i,k}(\sum\ k-min(k,a_j))\)，化简一下就是 $nf_{i,k}k-f_{i,k}\sum min(k,a_j) $，后面的和式是一个全局求和，我们可以预处理，然后把它当成一个系数，在线段树上维护 \(f_{i,k}\sum min(k,a_j)\)。
最后就是给前面倒水，其实和最开始更新 \(f\) 数组时一样，维护二维后缀和就行，具体实现可以用全局减部分。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 1e5+5,mod = 998244353;
#define A(x) (x>=mod?x-mod:x)
int n,a[N],mx,b[N];
LL ans[N],D,h[N],s[N],p1[N],p2[N],DD,D1;
inline LL qpow(LL a,int b)
{
LL res=1;
while(b)
{
if(b&1) res=res*a%mod;
a=a*a%mod; b>>=1;
}
return res;
}
inline int read()
{
int res=0; char x=getchar();
while(x>'9'||x<'0') x=getchar();
while(x>='0'&&x<='9') res=(res<<1)+(res<<3)+(x^48),x=getchar();
return res;
}
namespace SEG
{
struct T
{
int l,r; LL s1,s2,s3,lz;
inline void operator += (const T &x)
{
s1=A(s1+x.s1); s2=A(s2+x.s2); s3=A(s3+x.s3);
}
} tr[N<<2];
inline void pushup(int k)
{
tr[k].s1=A(tr[k<<1].s1+tr[k<<1|1].s1);
tr[k].s2=A(tr[k<<1].s2+tr[k<<1|1].s2);
tr[k].s3=A(tr[k<<1].s3+tr[k<<1|1].s3);
}
inline void pushdown(int k)
{
if(tr[k].lz!=1)
{
LL lz=tr[k].lz; tr[k].lz=1;
tr[k<<1].lz=(tr[k<<1].lz*lz)%mod;
tr[k<<1].s1=(tr[k<<1].s1*lz)%mod;
tr[k<<1].s2=(tr[k<<1].s2*lz)%mod;
tr[k<<1].s3=(tr[k<<1].s3*lz)%mod;
tr[k<<1|1].lz=(tr[k<<1|1].lz*lz)%mod;
tr[k<<1|1].s1=(tr[k<<1|1].s1*lz)%mod;
tr[k<<1|1].s2=(tr[k<<1|1].s2*lz)%mod;
tr[k<<1|1].s3=(tr[k<<1|1].s3*lz)%mod;
}
}
inline void bui(int k,int l,int r)
{
tr[k].l=l; tr[k].r=r; tr[k].lz=1;
if(l==r) return;
int mid=l+r>>1;
bui(k<<1,l,mid); bui(k<<1|1,mid+1,r);
}
inline void mdfj(int k,int p,int v)
{
if(tr[k].l==tr[k].r)
{
tr[k].s1=A(tr[k].s1+v); tr[k].s2=A(tr[k].s2+1ll*v*p%mod);
tr[k].s3=A(tr[k].s3+1ll*v*h[p]%mod);
return;
}
pushdown(k);
int mid=tr[k].l+tr[k].r>>1;
if(p<=mid) mdfj(k<<1,p,v);
else mdfj(k<<1|1,p,v);
pushup(k);
}
inline void mdfc(int k,int L,int R)
{
if(L>R) return;
if(tr[k].l>=L&&tr[k].r<=R)
{
tr[k].s1=(tr[k].s1*D1)%mod;
tr[k].s2=(tr[k].s2*D1)%mod;
tr[k].s3=(tr[k].s3*D1)%mod;
tr[k].lz=(tr[k].lz*D1)%mod;
return;
}
pushdown(k);
int mid=tr[k].l+tr[k].r>>1;
if(L<=mid) mdfc(k<<1,L,R);
if(R>mid) mdfc(k<<1|1,L,R);
pushup(k);
}
inline void mdfc(int k,int p)
{
if(tr[k].l==tr[k].r)
{
tr[k].s1=(tr[k].s1*D)%mod;
tr[k].s2=(tr[k].s2*D)%mod;
tr[k].s3=(tr[k].s3*D)%mod;
return;
}
pushdown(k);
int mid=tr[k].l+tr[k].r>>1;
if(p<=mid) mdfc(k<<1,p);
else mdfc(k<<1|1,p);
pushup(k);
}
inline T que(int k,int L,int R)
{
if(L>R) return {0,0,0,0,0,1};
if(tr[k].l>=L&&tr[k].r<=R) return tr[k];
pushdown(k);
int mid=tr[k].l+tr[k].r>>1; T res={0,0,0,0,0,1};
if(L<=mid) res+=que(k<<1,L,R);
if(R>mid) res+=que(k<<1|1,L,R);
// printf("%lld %lld %lld\n",res.s1,res.s2,res.s3);
return res;
}
} using namespace SEG;
int main()
{
freopen("bottle.in","r",stdin);
freopen("bottle.out","w",stdout);
n=read();
for(int i=1;i<=n;i++) a[i]=read(),mx=max(mx,a[i]),b[i]=a[i];
sort(b+1,b+1+n); for(int i=1;i<=n;i++) s[i]=A(s[i-1]+b[i]);
for(int j=1;j<=mx;j++)
{
int tmp=upper_bound(b+1,b+1+n,j)-b-1;
h[j]=(s[tmp]+1ll*j*(n-tmp)%mod)%mod;
}
D=qpow(n-1,mod-2); DD=D*D%mod; D1=A(D+1); bui(1,1,mx);
for(int i=1;i<=n;i++)
{
if(i==1) mdfj(1,a[i],n-1);
int tmp=0; T tt=que(1,1,a[i]),tot=tr[1];
if(i!=1)
{
tmp=que(1,a[i],a[i]).s1;
mdfj(1,a[i],(tot.s1-tt.s1+mod)%mod);
}
ans[i]=(ans[i]+n*(tt.s2+(tot.s1-tt.s1+mod)*a[i]%mod)%mod-(tt.s3+(tot.s1-tt.s1+mod)*h[a[i]]%mod)%mod+mod)%mod;
mdfc(1,1,a[i]-1); mdfc(1,a[i]); if(tmp) mdfj(1,a[i],tmp);//线段树含义：前缀和数组。
tt=que(1,1,a[i]-1); tot=tr[1];
p1[i]=tt.s2; p2[i]=A(1ll*tot.s1-tt.s1+mod);
}
for(int i=1;i<=n;i++)
{
T tmp=que(1,1,a[i]-1);
ans[i]=(ans[i]*DD)%mod,ans[i]=(ans[i]+(tmp.s2-p1[i]+mod)*D%mod+((1ll*tr[1].s1-tmp.s1+mod)-p2[i]+mod)*a[i]%mod*D%mod)%mod;
}
for(int i=1;i<=n;i++) printf("%lld\n",ans[i]);
return 0;
}
T cb
注意 \(O(n^3)\) 维护三维前缀和。
code
#include<bits/stdc++.h>
using namespace std;
#define mx(x,y) (x>y?x:y)
const int N = 260;
int s[N][N][N],n,k;
inline int cal(int x,int y,int z,int len)
{
int x1=x-len-1,y1=y-len-1,z1=z-len-1;
return s[x][y][z]-s[x][y][z1]-s[x][y1][z]-s[x1][y][z]+s[x1][y1][z]+s[x1][y][z1]+s[x][y1][z1]-s[x1][y1][z1];
}
bool check(int mid)
{
for(int i=1;i<N-mid;i++)
for(int j=1;j<N-mid;j++)
for(int h=1;h<N-mid;h++)
if(cal(i+mid,j+mid,h+mid,mid)>=k) return 1;
return 0;
}
int main()
{
freopen("rgb.in","r",stdin);
freopen("rgb.out","w",stdout);
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++)
{
int x,y,z; scanf("%d%d%d",&x,&y,&z); x++,y++,z++;
s[x][y][z]+=1;
}
for(int i=1;i<N;i++)
for(int j=1;j<N;j++)
for(int h=1;h<N;h++)
s[i][j][h]+=s[i][j][h-1]+s[i-1][j][h]+s[i][j-1][h]-s[i-1][j-1][h]-s[i-1][j][h-1]-s[i][j-1][h-1]+s[i-1][j-1][h-1];
int l=1,r=N-1,res=1;
while(l<=r)
{
int mid=l+r>>1;
if(check(mid)) res=mid,r=mid-1;
else l=mid+1;
}
printf("%d\n",res);
return 0;
}
T by
直接贪心就做完啦！
但是你要贪对。。。
记得打拍。
code
#include<bits/stdc++.h>
using namespace std;
#define P pair<int,int>
#define fi first
#define se second
const int N = 1e3+5;
int T,n,a[N],b[N];
int top;
P st[N*N];
int main()
{
freopen("sort.in","r",stdin);
freopen("sort.out","w",stdout);
scanf("%d",&T);
while(T--)
{
top=0;
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int j=1;j<=n;j++) scanf("%d",&b[j]);
bool fl=0;
for(int i=n;i>=1;i--)
{
if(a[i]==b[i]) continue;
if(b[i]<a[i]) {fl=1; break;}
while(b[i]>a[i])
{
int l=i-1;
while(l>1&&a[l]!=b[i])
{
if(a[l]>b[i]) {fl=1; break;}
l--;
}
if(fl) break;
for(int j=l+1;j<=i;j++) st[++top]={j-1,j},swap(a[j],a[j-1]);
if(a[i]>b[i]) {fl=1; break;}
}
if(fl) break;
}
if(fl) printf("-1\n");
else
{
printf("%d\n%d\n",0,top);
for(int i=1;i<=top;i++) printf("%d %d\n",st[i].fi,st[i].se);
}
}
return 0;
}
T 人
考虑某些数位 dp 可以用容斥解决。计算前 \(i\) 位没有限制的答案，最后答案就是从高到低按位加入限制。
设数位之和是 \(s\)，之前有 \(p\) 位，\(\sum_{k=0}^p\ (-1)^k\binom{p}{k}\binom{s-km+p-1}{p-1}\)（插板+二项式反演）。
然后就做完啦！
code
#include<bits/stdc++.h>
using namespace std;
const int N = 2e3+5,mod = 1e9+7;
int fac[N*N],inv[N*N],m,L,a[N],sum;
long long ans;
inline int C(int x,int y)
{
if(x<y) return 0;
return 1ll*fac[x]*inv[x-y]%mod*inv[y]%mod;
}
int main()
{
freopen("dba.in","r",stdin);
freopen("dba.out","w",stdout);
scanf("%d%d",&m,&L);
for(int i=1;i<=L;i++) scanf("%d",&a[i]),sum+=a[i];
fac[0]=fac[1]=inv[0]=inv[1]=1;
for(int i=2;i<=(m-1)*L;i++) fac[i]=1ll*fac[i-1]*i%mod,inv[i]=1ll*(mod-mod/i)*inv[mod%i]%mod;
for(int i=2;i<=(m-1)*L;i++) inv[i]=1ll*inv[i-1]*inv[i]%mod;
for(int p=1;p<=L;p++)
{
for(int i=0;i<=L-p;i++)
{
ans=((ans+1ll*(i&1?(-1):(1))*C(L-p,i)*((1ll*C(sum-m*i+L-p,L-p)-C(sum-m*i+L-p-a[p],L-p)+mod)%mod)+mod)+mod)%mod;
}
sum-=a[p];
}
printf("%lld\n",ans);
return 0;
}
T 01
trick：二进制比较大小可以用 hash + 二分。
注意最优情况只会有两种情况：
-
前 \(k-1\) 个数都是 \(0\) 那么从第一个 \(1\) 开始选到最后一定最优，组合数可求方案数。
-
剩下的情况，一定是选 \(n-k+1\) 个连续的最优。
考虑后面的怎么做。
我们已经知道长度了，可以枚举找到最大的串（上面的 trick，hash + 二分），注意这里不需要比较最后一位，原因显然。
然后做完啦！
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 2e6+5,B = 233,mod = 998244353;
int n,k,s[N],m;
namespace BF
{
int fac[N],inv[N];
inline int C(int x,int y)
{
if(x<y) return 0;
return 1ll*fac[x]*inv[x-y]%mod*inv[y]%mod;
}
void work()
{
fac[0]=fac[1]=inv[0]=inv[1]=1;
for(int i=2;i<=n;i++) fac[i]=1ll*fac[i-1]*i%mod,inv[i]=1l*(mod-mod/i)*inv[mod%i]%mod;
for(int i=2;i<=n;i++) inv[i]=1ll*inv[i]*inv[i-1]%mod;
int l=1;
while(l<n&&!s[l]) l++; l--;
int cnt=0,ans=0;
for(int i=k-1;i<=l;i++) cnt=(cnt+C(l,i))%mod;
if(s[l+1]==1)
for(int i=l;i<=n;i++) ans=(ans*2ll+s[i])%mod;
printf("%d %d\n",ans,cnt);
}
}
namespace ZJ
{
const int Mod = 1e9+3579;
LL hs[N],p[N];
inline LL get(int l,int r) {return (hs[r]+Mod-hs[l-1]*p[r-l+1]%Mod)%Mod;}
int check(int l1,int l2)
{
int l=1,r=m-1,res=1;
while(l<=r)
{
int mid=l+r>>1;
if(get(l1,l1+mid-1)!=get(l2,l2+mid-1)) res=mid,r=mid-1;
else l=mid+1;
}
if(s[l1+res-1]==s[l2+res-1]) return -1;
if(s[l1+res-1]<s[l2+res-1]) return 1;
else return 0;
}
void work()
{
p[0]=1; for(int i=1;i<=n;i++) hs[i]=(hs[i-1]*B+s[i])%Mod,p[i]=p[i-1]*B%Mod;
int al=1,cnt=1,ans=0,tmp=0;
for(int i=2;i+m-1<=n;i++)
{
int jd=check(al,i);
if(jd==1) cnt=1,al=i;
if(jd==-1) cnt++;
}
for(int i=1;i<=n;i++)
{
if(i>=al&&i<=al+m-1) tmp=(tmp*2ll+s[i])%mod;
else ans=(ans+s[i])%mod;
}
ans=(ans+tmp)%mod;
printf("%d %d\n",ans,cnt);
}
}
int main()
{
freopen("divide.in","r",stdin);
freopen("divide.out","w",stdout);
scanf("%d%d",&n,&k); m=n-k+1;
for(int i=1;i<=n;i++) scanf("%1d",&s[i]);
if(n==k)
{
int ans=0;
for(int i=1;i<=n;i++) ans+=s[i];
printf("%d %d\n",ans,1); return 0;
}
bool fl=0;
for(int i=1;i<=k;i++) if(s[i]) {fl=1; break;}
if(!fl) BF::work();
else ZJ::work();
return 0;
}
T lantern
抽象 dp。
首先发现性质：任何时刻灯笼的可达范围一定是一个区间。
（下文值域指山的高度及灯笼的范围，序列指山。）
所以设计状态 \(f_{x,y}\) 表示值域可达范围为 \([x,y]\)。好像就能有分了？
要求 \([1,k]\) 以每个灯笼为起点的答案，有一个很自然的想法就是倒序做，初始状态是所有能到 \([1,n]\) 的状态。
每次删去 \(x/y\) 的边界处的灯笼，然后得到一个区间更小的状态。
发现转移不可做，无法根据序列上的灯笼更新值域上的状态。
于是改变状态。设 \(f_{x,y}\) 表示当前有的灯笼 \(x\) 和 \(y\)，可达区间为 \([a_x,b_y]\)（注意这样设计状态有很多不合法状态或一定不优状态，转移时要舍掉）。
然后我们的目的就是将值域和序列联系起来，也就是能否通过某个值域区间，确定可达的序列区间。
发现如果有一个出发点是确定的，那么显然可以。
我们想知道对于每一个点，在任意值域区间上可达的序列上的范围。
太菜了。不会。考虑转化，我们只需要判断是否可达，所以可以记录从一个点向左、右扩展所需的值域上的范围为多少，最后取交即可。
终于可以开始转移了，区间一定是从大到小转移，所以我们将所有灯笼按 \(a\) 升序，\(b\) 降序排序，两层循环一层正序一层倒序（实际处理可以直接开桶）。
三种情况，都是考虑值域上。
由于一直是用大区间更新小区间，所以可以开堆记录大区间中的最优状态，然后更新。
能更新的条件就是当前删去的灯笼值域上有交，序列上可达。（这两个都很好做）
堆开两个，压堆的时候压两个，分别表示删 \(x\)，\(y\)。
最后考虑第三种转移，我们知道 \([x,x]\) 时，其他那些非法的 \([x,y]\)（就是 \(y\) 的 \(b_y\) 小于 \(x\) 的 \(b_y\)，你的状态写的是 \([x,y]\) 但实际上 \(y\) 根本不能成为边界，所以这种状态没用）可以被我们当成中间状态来转移。也就是每次碰到这种状态直接更新成 \(f_{x,x}/f_{y,y}\)，然后就变成前两种问题了。
大体上就是这样，初值是 \(\infty\) 或 \(0\)（序列可达范围到了 \([1,n]\)）。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 2e3+5;
const LL inf = 1e18;
int n,k,h[N];
struct D {int p,c,a,b;} d[N]; vector<int> l[N],r[N];
LL f[N][N];
struct L {int l,r;} ll[N][N];
struct P
{
int p; LL d;
bool operator < (const P &x) const {return d>x.d;}
};
priority_queue<P> q[2][N];
int main()
{
freopen("lantern.in","r",stdin);
freopen("lantern.out","w",stdout);
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++) scanf("%d",&h[i]);
for(int i=1;i<=k;i++) scanf("%d%d%d%d",&d[i].p,&d[i].c,&d[i].a,&d[i].b),l[d[i].a].push_back(i),r[d[i].b].push_back(i);
for(int i=1;i<=k;i++)
{
int p=d[i].p;
ll[i][p]={h[p],h[p]};
for(int j=p-1;j>=1;j--) ll[i][j]={min(ll[i][j+1].l,h[j]),max(ll[i][j+1].r,h[j])};
for(int j=p+1;j<=n;j++) ll[i][j]={min(ll[i][j-1].l,h[j]),max(ll[i][j-1].r,h[j])};
}
for(int oo=1;oo<=n;oo++) for(int x:l[oo])
for(int o=n;o>=oo;o--) for(int y:r[o])
{
int L=min(d[x].a,d[y].a),R=max(d[x].b,d[y].b);
f[x][y]=inf;
if(!(ll[x][d[x].p].l>=L&&ll[x][d[x].p].r<=R)||!(ll[x][d[y].p].l>=L&&ll[x][d[y].p].r<=R)) continue;
if(d[y].a<d[x].a&&d[y].b<d[x].b) continue;
if(ll[x][1].l>=L&&ll[x][n].l>=L&&ll[x][1].r<=R&&ll[x][n].r<=R) f[x][y]=0;
else if(d[x].a>d[y].a) f[x][y]=f[y][y];
else if(d[x].b>d[y].b) f[x][y]=f[x][x];
else
{
while(!q[1][x].empty())
{
P tmp=q[1][x].top();
if(d[tmp.p].a<=R&&(ll[x][d[tmp.p].p].l>=L&&ll[x][d[tmp.p].p].r<=R)) {f[x][y]=min(tmp.d,f[x][y]); break;}
else q[1][x].pop();
}
while(!q[0][y].empty())
{
P tmp=q[0][y].top();
if(d[tmp.p].b>=L&&ll[x][d[tmp.p].p].l>=L&&ll[x][d[tmp.p].p].r<=R) {f[x][y]=min(tmp.d,f[x][y]); break;}
else q[0][y].pop();
}
}
if(f[x][y]<inf)
{
q[1][x].push({y,f[x][y]+d[y].c});
q[0][y].push({x,f[x][y]+d[x].c});
}
}
for(int i=1;i<=k;i++) printf("%lld\n",f[i][i]>=inf?(-1):(f[i][i]+d[i].c));
return 0;
}
T TRIE
容易想到 trie，但是具体维护啥众说纷纭。
trick：相乘小于 \(0\) 转化成异号，异号可以想到零点存在定理。
其实很显然，在两个异号的位置之间一定有一个转折点。
也就是只要找到一组异号的，无论相不相邻，我们都可以二分，每次算中点的符号，然后将区间缩小成一半，满足两个端点依旧异号。
维护一个异或最大值和最小值，然后就做完了。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
#define fi first
#define se second
const int N = 1e6+5,M = 6e3+5;
#define cal(i,x,y) ((a[i]^x)-y)
#define check(x,y,z,w) (((cal(x,z,w)<=0&&cal(y,z,w)>0)||(cal(x,z,w)>0&&cal(y,z,w)<=0)))
int n,q;
int a[N];
namespace Trie
{
int son[N<<5][2],num,va[N<<5];
inline void ins(int x,int id)
{
int now=0;
for(int i=30;i>=0;i--)
{
bool c=((x>>i)&1);
if(!son[now][c]) son[now][c]=++num;
now=son[now][c];
}
va[now]=id;
}
inline int quemx(int x)
{
int now=0;
for(int i=30;i>=0;i--)
{
int c=((x>>i)&1);
if(son[now][c^1]) now=son[now][c^1];
else now=son[now][c];
}
return va[now];
}
inline int quemi(int x)
{
int now=0;
for(int i=30;i>=0;i--)
{
int c=((x>>i)&1);
if(son[now][c]) now=son[now][c];
else now=son[now][c^1];
}
return va[now];
}
} using namespace Trie;
inline int read()
{
int res=0; char x=getchar();
while(x>'9'||x<'0') x=getchar();
while(x>='0'&&x<='9') res=(res<<1)+(res<<3)+(x^48),x=getchar();
return res;
}
int main()
{
freopen("fun.in","r",stdin);
freopen("fun.out","w",stdout);
n=read(); q=read();
for(int i=1;i<=n;i++) a[i]=read(),ins(a[i],i);
while(q--)
{
int x=read(),y=read();
int mx=quemx(x),mi=quemi(x);
if(cal(mx,x,y)<0||cal(mi,x,y)>0) {printf("-1\n"); continue;}
int l=mx,r=mi; if(l>r) swap(l,r);
if(cal(l,x,y)==0) {printf("%d\n",l); continue;}
if(cal(r,x,y)==0) {printf("%d\n",r-1); continue;}
if(l==r-1) {printf("%d\n",l); continue;}
while(l<r-1)
{
int mid=l+r>>1;
if(cal(mid,x,y)==0) {printf("%d\n",mid); break;}
if(check(l,mid,x,y)) r=mid;
else l=mid;
if(l==r-1) {printf("%d\n",l); break;}
}
}
return 0;
}
