线性基
线性基
第 \(n+1\) 次学线性基,希望这次能学会。
模板
线性基通常用来处理异或相关的问题。
假如有 \(n\) 个数,我们想表示它们能相互异或得到的所有数组成的集合。
线性基就是针对这组数生成的集合,它们任意异或得到数的值域与原序列相同,并且满足是一个极小集合(数尽量少)。
联想基向量,这里每一个二进制位可以看成一维,线性基就是一组基向量。(好像叫极大线性无关组)
插入一个数的过程:
假如我们想插入 \(x\),\(a_i\) 表示二进制位第二位的基底,如果已经存在基底,那么 \(x \gets x \oplus a_i\),否则 \(a_i \gets x\)。
因为 \(a \oplus b \oplus a = b\),所以不妨令 \(c = a \oplus b\),这样仍能得到 \(b\)。上面的过程其实就是这样。
对于这道题,求最大值,直接贪心从高位向低位取,但注意我们取了高位时不知道包不包含低位(第 \(i\) 位的基底只保证最高是 \(i\),不保证没有低位)。
所以注意判断只有异或后会使答案变大才要。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 60;
#define LL long long
int n; LL ck[N];
inline void ins(LL x)
{
for(int i=55;i>=0;i--)
if((x>>i)&1)
{
if(!ck[i]) {ck[i]=x; break;}
x^=ck[i];
}
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
LL x; scanf("%lld",&x);
ins(x);
}
LL ans=0;
for(int i=55;i>=0;i--) if((ans^ck[i])>ans) ans^=ck[i];
printf("%lld\n",ans);
return 0;
}
彩灯
假如找到 \(cnt\) 个基底,那能异或得到的数的个数就是 \(2^{cnt}\)(每一个可选可不选,并且一定不会有重复的数)。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 60;
int n,m;
LL ck[N+5],ans;
void ins(LL x)
{
for(int j=n-1;j>=0;j--)
if((x>>j)&1)
{
if(!ck[j]) {ck[j]=x; ans++; break;}
x^=ck[j];
}
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
LL x=0;
for(int j=n-1;j>=0;j--)
{
char c; scanf(" %c",&c);
if(c=='O') x|=1ll<<j;
}
ins(x);
}
printf("%lld\n",(1ll<<ans)%2008);
return 0;
}
元素
直接贪心,按价值从大到小排序,如果能插入线性基就算贡献,否则不算。
首先,由于线性基是一个 极大线性无关组,也就是 任意子集异或和不为零,所以能插进去说明异或和不为零。
贪心证明:
假设最大的数是 \(a_n\),但 \(a_n\) 不在最终答案中,最终答案为集合 \(A\)。
那必然有 \(a_n=\bigoplus_{a_j \in A} a_j\),交换任意一个 \(a_j\) 和 \(a_n\) 等式仍成立且更优。所以一定选 \(a_n\)
(问:拟阵是啥?)
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 1e3+5;
int n,ans;
LL ck[62];
struct A {int v; LL num;} a[N];
void ins(LL x,int v)
{
for(int i=60;i>=0;i--)
if((x>>i)&1)
{
if(!ck[i]) {ans+=v; ck[i]=x; break;}
x^=ck[i];
}
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%lld%d",&a[i].num,&a[i].v);
sort(a+1,a+1+n,[&] (A &x,A &y) {return x.v>y.v;});
for(int i=1;i<=n;i++)
{
ins(a[i].num,a[i].v);
}
printf("%d\n",ans);
return 0;
}
新Nim游戏
转化问题,先手想赢,那么先手拿完剩下的集合的任意子集异或和不为零。
发现先把较大的数插进去,组成一个极大线性无关组,剩下的拿走即可。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 105;
int n; LL a[N],ans,ck[N];
void ins(LL x,LL v)
{
for(int i=30;i>=0;i--)
if((x>>i)&1)
{
if(!ck[i]) {ck[i]=x; return;}
x^=ck[i];
}
ans+=v;
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
sort(a+1,a+1+n,greater<int>());
for(int i=1;i<=n;i++) ins(a[i],a[i]);
printf("%lld\n",ans);
return 0;
}
XOR
第 k 小板子。
发现原有的线性基不太好确定一个数在值域值域中的位置,我们试着把它转化为一个好看的形式。
为了有一个标准,我们令每个二进制位都只在它这位的基底上出现,其他的直接异或掉。
这样第 \(i\) 位基底恰好就是第 \(2^i\) 小的数,我们将 \(k\) 二进制拆分后发现它们的意义恰好完全一样。
code
#include<stdio.h>
#include<cstring>
using namespace std;
#define LL long long
const int N = 1e4+5;
int T,tot,n,q,m;
LL ck[65],tmp[65],cnt;
inline void ins(LL x)
{
for(int i=60;i>=0;i--)
if((x>>i)&1)
{
if(!ck[i]) {ck[i]=x; m++; return;}
x^=ck[i];
}
}
void init()
{
cnt=0;
for(int i=0;i<=60;i++)
{
if(!ck[i]) continue;
for(int j=i-1;j>=0;j--)
if((ck[i]>>j)&1) ck[i]^=ck[j];
tmp[cnt++]=ck[i];
}
}
inline LL que(LL k)
{
k-=(n!=m); if(!k) return 0;
if(k>=(1ll<<cnt)) return -1;
LL res=0;
for(int i=0;i<cnt;i++)
if((k>>i)&1) res^=tmp[i];
return res;
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&T);
while(T--)
{
memset(ck,0,sizeof(ck)); m=0;
printf("Case #%d:\n",++tot);
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
LL x; scanf("%lld",&x),ins(x);
}
init();
scanf("%d",&q);
while(q--)
{
LL x; scanf("%lld",&x);
printf("%lld\n",que(x));
}
}
return 0;
}
Operation
不是板。
容易想到扫描线处理出每一个右端点的答案。
因为线性基的时间空间都是 \(log\) 的,我们不妨直接开 \(a_{i,r}\) 表示第 \(i\) 位,右端点到 \(r\) 的线性基。
考虑如何确定左端点。
直接贪心(线性基和贪心最配?),对基底,我们只在乎这一位能否被表出,而不在乎基底的值,所以尽量选靠右的肯定最优。
单独开一个 \(pos_{i,r}\) 记录当前基底的位置,如果新加进来的更靠右,那么替换,继续判断被换下来的基能否往后插。
插入直接做就好了。
code
#include<stdio.h>
#include<cmath>
#include<algorithm>
using namespace std;
#define LL long long
const int N = 5e5+5;
int T,n,m;
int ck[N][32],pos[N][32];
void ins(int k,int x,int p)
{
for(int i=30;i>=0;i--)
if((x>>i)&1)
{
if(!ck[k][i]) {ck[k][i]=x; pos[k][i]=p; break;}
else
{
if(pos[k][i]<p) swap(ck[k][i],x),swap(pos[k][i],p);
x^=ck[k][i];
}
}
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&T);
while(T--)
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
int x; scanf("%d",&x);
for(int j=0;j<=30;j++) ck[i][j]=ck[i-1][j],pos[i][j]=pos[i-1][j];
ins(i,x,i);
}
int ans=0;
while(m--)
{
int c,l,r; scanf("%d%d",&c,&l);
if(c==0)
{
scanf("%d",&r);
l=(l^ans)%n+1; r=(r^ans)%n+1;
if(l>r) swap(l,r);
ans=0;
for(int i=30;i>=0;i--)
if(pos[r][i]>=l&&(ans^ck[r][i])>ans) ans^=ck[r][i];
printf("%d\n",ans);
}
else
{
l=l^ans; n++;
for(int i=0;i<=30;i++) ck[n][i]=ck[n-1][i],pos[n][i]=pos[n-1][i];
ins(n,l,n);
}
}
}
return 0;
}
Ivan and Burgers
同上
code
#include<stdio.h>
#include<cmath>
#include<algorithm>
using namespace std;
#define LL long long
const int N = 5e5+5;
int T,n,m;
int ck[N][21],pos[N][21];
void ins(int k,int x,int p)
{
for(int i=20;i>=0;i--)
if((x>>i)&1)
{
if(!ck[k][i]) {ck[k][i]=x; pos[k][i]=p; break;}
else
{
if(pos[k][i]<p) swap(ck[k][i],x),swap(pos[k][i],p);
x^=ck[k][i];
}
}
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
int x; scanf("%d",&x);
for(int j=0;j<=20;j++) ck[i][j]=ck[i-1][j],pos[i][j]=pos[i-1][j];
ins(i,x,i);
}
scanf("%d",&m);
while(m--)
{
int l,r,ans=0; scanf("%d%d",&l,&r);
for(int i=20;i>=0;i--)
if(pos[r][i]>=l&&(ans^ck[r][i])>ans) ans^=ck[r][i];
printf("%d\n",ans);
}
return 0;
}
最大XOR和路径
图论。
感觉难点不在线性基,重点理解异或的性质。
从简单的情况考虑,即只有一条链,肯定都选。
假如在这条链之外有环怎么办。(链不可能和环有重边,如果有,重边异或后不会有贡献,又变成链了。)
考虑走到环又走回来,中间的路径走了两边,异或后没了,所以选环就相当于选了一个单独的环。
所以我们找出 \(1 \to n\) 的链的异或和,再插入所有环的,找最大即可。
一条路径走两遍相当于没走!
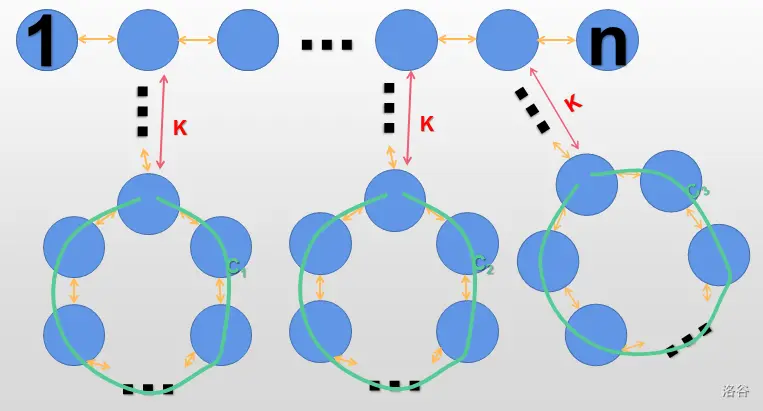
图片来自:【[WC2011]最大XOR和路径】。
code
#include<cstdio>
#include<math.h>
#include<algorithm>
#include<cstring>
using namespace std;
#define LL long long
const int N = 5e4+5,M = 1e5+5;
int n,m;
int head[N],tot; LL d[N];
struct E {int u,v; LL w;} e[M<<1];
inline void add(int u,int v,LL w) {e[++tot]={head[u],v,w}; head[u]=tot;}
bool vs[N];
LL ck[70];
inline void ins(LL x)
{
for(int i=62;i>=0;i--)
if((x>>i)&1)
{
if(!ck[i]) {ck[i]=x; break;}
x^=ck[i];
}
}
void dfs(int u,int f,LL res)
{
d[u]=res; vs[u]=1;
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v;
if(!vs[v]) dfs(v,u,res^e[i].w);
else ins(res^e[i].w^d[v]);
}
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int x,y; LL z; scanf("%d%d%lld",&x,&y,&z);
add(x,y,z); add(y,x,z);
}
dfs(1,0,0ll);
LL ans=d[n];//主链的贡献
for(int i=62;i>=0;i--) if((ans^ck[i])>ans) ans^=ck[i];
printf("%lld\n",ans);
return 0;
}
幸运数字
如果你知道线性基能在 \(log^2(t)\) 的复杂度内合并,就做完了。
先树剖转化为区间问题,发现就是若干个区间求异或最大值,区间内异或最大值同上。
最后将若干个区间的线性基合并,求最大值就行了。
复杂度 \(q\log(n)\log^2(t)\),vjudge 最优解。(你永远可以相信树剖)
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N =2e4+5;
int n,q,pos[N][62];
LL a[N],ck[N][62];
int head[N],tot;
struct E {int u,v;} e[N<<1];
inline void add(int u,int v) {e[++tot]={head[u],v}; head[u]=tot;}
inline void ins(LL x,int k,int p)
{
for(int i=61;i>=0;i--)
if((x>>i)&1)
{
if(!ck[k][i]) {ck[k][i]=x; pos[k][i]=p; break;}
else
{
if(pos[k][i]<p) swap(pos[k][i],p),swap(ck[k][i],x);
x^=ck[k][i];
}
}
}
int sz[N],son[N],top[N],dfn[N],num,rk[N],fa[N],dep[N];
void dfs1(int u,int f)
{
fa[u]=f; sz[u]=1; son[u]=-1; dep[u]=dep[f]+1;
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v; if(v==f) continue;
dfs1(v,u); sz[u]+=sz[v];
if(son[u]==-1||sz[son[u]]<sz[v]) son[u]=v;
}
}
void dfs2(int u,int t)
{
top[u]=t; dfn[u]=++num; rk[num]=u;
if(son[u]==-1) return;
dfs2(son[u],t);
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v; if(v==fa[u]||v==son[u]) continue;
dfs2(v,v);
}
}
LL tmp[62];
inline void merge(int l,int r)
{
for(int i=61;i>=0;i--)
{
if(pos[r][i]>=l)
{
LL tt=ck[r][i];
for(int j=i;j>=0;j--)
if((tt>>j)&1)
{
if(!tmp[j]) {tmp[j]=tt; break;}
tt^=tmp[j];
}
}
}
}
inline LL que(int x,int y)
{
LL res=0;
memset(tmp,0,sizeof(tmp));
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]]) swap(x,y);
merge(dfn[top[x]],dfn[x]);
x=fa[top[x]];
}
if(dfn[x]>dfn[y]) swap(x,y);
merge(dfn[x],dfn[y]);
for(int i=61;i>=0;i--) if((res^tmp[i])>res) res^=tmp[i];
return res;
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d",&n,&q);
for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
for(int i=1;i<n;i++)
{
int x,y; scanf("%d%d",&x,&y);
add(x,y); add(y,x);
}
dfs1(1,0); dfs2(1,1);
for(int i=1;i<=n;i++)
{
for(int j=0;j<=61;j++) ck[i][j]=ck[i-1][j],pos[i][j]=pos[i-1][j];
ins(a[rk[i]],i,i);
}
while(q--)
{
int l,r; scanf("%d%d",&l,&r);
printf("%lld\n",que(l,r));
}
return 0;
}
欧几里得的噩梦
题面

不需要线性基,但是题目本身就是在模拟线性基插入的过程。
性质很明显,每个二进制数只有两位是 \(1\),所以直接将这两位连边(只有一位那就和虚点连)。
显然如果成环了就不是最小的子集了,所以模拟生成树的过程加边就行。答案就是选了多少边。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5+5,mod = 1e9+7;
int n,m;
int fa[N],cnt;
inline long long qpow(long long a,int b)
{
long long res=1;
while(b)
{
if(b&1) res=res*a%mod;
a=a*a%mod; b>>=1;
}
return res;
}
inline int find(int x) {return x==fa[x]?(x):(fa[x]=find(fa[x]));}
vector<int> v;
int main()
{
freopen("Euclid.in","r",stdin);
freopen("Euclid.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=m+1;i++) fa[i]=i;
for(int i=1;i<=n;i++)
{
int c,x,y=m+1; scanf("%d%d",&c,&x);
if(c==2) scanf("%d",&y);
int fx=find(x),fy=find(y);
if(fx==fy) continue;
fa[fx]=fy; cnt++;
v.push_back(i);
}
sort(v.begin(),v.end());
printf("%lld %d\n",qpow(2,cnt),cnt);
for(int i:v) printf("%d ",i);
return 0;
}
装备购买
真·线性基
上面的题都是二进制下的线性基来处理异或问题,而真正的线性基其实是实数范围内的。
容易看出本题仍是求一个极大线性无关组。考虑如何将一个向量插入线性基。
类比二进制下的异或操作,我们插入的过程其实就是想消掉某一位。实数意义下的异或其实就是加减法。
假如对于向量 \(\bm{a}\)(\(\bm{a}_i\) 表示第 \(i\) 维的值),我们在第 \(i\) 维已经有了基底 \(\bm{c}\),那么想要消去 \(\bm{a}\) 的第 \(i\) 维,即 \(\bm{a} \gets \bm{a}-\frac{\bm{a}_i}{\bm{c}_i} \times \bm{c}\)。
其他操作和线性基一样。注意精度问题。
code
#include<bits/stdc++.h>
using namespace std;
#define LD long double
const int N = 505;
const LD del = 1e-7;
int n,m; long long ans,cnt;
struct A {int w; vector<LD> p;} a[N];
int ck[N];
inline void ins(int x)
{
for(int j=m-1;j>=0;j--)
{
if(fabs(a[x].p[j])>del)
{
if(!ck[j]) {ck[j]=x; cnt++; ans+=a[x].w; break;}
LD tmp=a[x].p[j]/a[ck[j]].p[j];
for(int k=j;k>=0;k--) a[x].p[k]-=tmp*a[ck[j]].p[k];
}
}
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
a[i].p.resize(m);
for(int j=0;j<m;j++) scanf("%Lf",&a[i].p[j]);
}
for(int i=1;i<=n;i++) scanf("%d",&a[i].w);
sort(a+1,a+1+n,[&] (const A &x,const A &y) {return x.w<y.w;});
for(int i=1;i<=n;i++) ins(i);
printf("%d %lld\n",cnt,ans);
return 0;
}
圣剑护符
好题捏。
容易想到树剖。发现如果路径上的数全能插进线性基,那么它一定是线性无关的,也就是不合法。
一开始想维护线性基大小,发现修改不太可做。
发现有一个很好的性质:如果多于 \(30\) 个数一定线性相关,鸽笼易证。
所以我们需要解决的就是小于三十个数是否线性相关,直接暴力插。
对于区间修改,差分!!!(总是想不到差分),用个树状数组维护一下就好了。(异或也可以用树状数组维护)
code
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+5;
int n,q;
int head[N],tot,a[N];
struct E{int u,v;} e[N<<1];
inline void add(int u,int v) {e[++tot]={head[u],v}; head[u]=tot;}
int sz[N],top[N],son[N],fa[N],dep[N],num,rk[N],dfn[N];
void dfs1(int u,int f)
{
fa[u]=f; dep[u]=dep[f]+1; sz[u]=1; son[u]=-1;
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v; if(v==f) continue;
dfs1(v,u); sz[u]+=sz[v];
if(son[u]==-1||sz[son[u]]<sz[v]) son[u]=v;
}
}
void dfs2(int u,int t)
{
top[u]=t; dfn[u]=++num; rk[num]=u;
if(son[u]==-1) return;
dfs2(son[u],t);
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v; if(v==fa[u]||v==son[u]) continue;
dfs2(v,v);
}
}
inline int lca(int x,int y)
{
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]]) swap(x,y);
x=fa[top[x]];
}
if(dfn[x]>dfn[y]) swap(x,y);
return x;
}
namespace BIT
{
int c[N];
inline void _mdf(int x,int v) {for(;x<=n;x+=(x&-x)) c[x]^=v;}
inline int que(int x) {int res=0; for(;x;x-=(x&-x)) res^=c[x]; return res;}
inline void mdf(int l,int r,int v) {_mdf(l,v); _mdf(r+1,v);}
} using namespace BIT;
int tmp[31];
bool ins(int l,int r)
{
for(int i=l;i<=r;i++)
{
bool fl=0; int x=que(i);
for(int j=30;j>=0;j--)
if((x>>j)&1)
{
if(!tmp[j]) {tmp[j]=x; fl=1; break;}
x^=tmp[j];
}
if(!fl) return 1;
}
return 0;
}
bool inspath(int x,int y)
{
memset(tmp,0,sizeof(tmp));
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]]) swap(x,y);
if(ins(dfn[top[x]],dfn[x])) return 1;
x=fa[top[x]];
}
if(dfn[x]>dfn[y]) swap(x,y);
if(ins(dfn[x],dfn[y])) return 1;
return 0;
}
void mdfpath(int x,int y,int z)
{
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]]) swap(x,y);
mdf(dfn[top[x]],dfn[x],z);
x=fa[top[x]];
}
if(dfn[x]>dfn[y]) swap(x,y);
mdf(dfn[x],dfn[y],z);
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d",&n,&q);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<n;i++)
{
int x,y; scanf("%d%d",&x,&y);
add(x,y); add(y,x);
}
dfs1(1,0); dfs2(1,1);
for(int i=1;i<=n;i++) _mdf(i,a[rk[i]]^a[rk[i-1]]);
// for(int i=1;i<=n;i++) printf("%d ",que(i)); putchar('\n');
while(q--)
{
string c; cin>>c;
if(c[0]=='Q')
{
int x,y; scanf("%d%d",&x,&y);
int l=lca(x,y),dis=dep[x]+dep[y]-(dep[l]<<1)+1;
if(dis>30) printf("YES\n");
else
{
if(inspath(x,y)) printf("YES\n");
else printf("NO\n");
}
}
else
{
int x,y,z; scanf("%d%d%d",&x,&y,&z);
mdfpath(x,y,z);
}
}
return 0;
}
FCT
线性基高级应用——二元组线性基。
详见链接。


