2024.9.28 模拟赛 CSP6

合集 - 模拟赛(28)
1.2024.7.18模拟赛12.2024.7.19模拟赛23.2024.7.20模拟赛34.2024.7.21模拟赛45.2024.7.22模拟赛56.2024.7.23 模拟赛67.2024.7.25模拟赛78.2024.7.26模拟赛89.2024.7.27模拟赛910.2024.7.28 模拟赛1011.2024.7.29模拟赛1112.2024.7.31模拟赛1213.2024.8.1 模拟赛1314.2024.8.6 模拟赛 1415.2024.8.7 模拟赛 1516.2024.8.8模拟赛1617.2024.8.10模拟赛1718.2024.8.18 模拟赛 2219.2024.8.19 模拟赛 2420.小集训21.2024.9.23 模拟赛 CSP 322.2024.9.24 模拟赛 CSP423.2024.9.25 模拟赛 多校24.2024.9.27 模拟赛 CSP5
25.2024.9.28 模拟赛 CSP6
26.2024.9.30 模拟赛 CSP727.2024.10.7 模拟赛 多校328.2024.？.？？ 模拟赛 ？？？
收起

模拟赛

树剖 yyds

T1 一般图最小匹配

简单 dp，水。O(n2)

其实也是可反悔贪心的板子，可以 O(nlog⁡(n)) 做。

考虑排序后求差分数组，就变成不能选相邻的。然后就是可反悔贪心板子。

用双向链表（记录前驱后继）维护，然后放进堆里。

板

dp 
#include<bits/stdc++.h>
using namespace std;
#define ab(x) ((x>=0)?(x):(-x))
#define mi(x,y) ((x>y)?(y):(x))
#define LL long long
const int N = 5005;
int n,m;
LL f[2][N][2],a[N];

int main()
{
	freopen("match.in","r",stdin);
	freopen("match.out","w",stdout);
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
	sort(a+1,a+1+n);
	memset(f,0x3f,sizeof(f));
	f[0][1][1]=ab(a[2]-a[1]); f[0][0][0]=0;
	for(int i=3;i<=n;i++)
	{
		f[i&1][0][0]=0;
		for(int j=1;j<=i>>1;j++)
		{
			f[i&1][j][1]=f[(i-1)&1][j-1][0]+ab(a[i]-a[i-1]);
			f[i&1][j][0]=mi(f[(i-1)&1][j][0],f[(i-1)&1][j][1]);
		}
	}
	printf("%lld\n",mi(f[n&1][m][0],f[n&1][m][1]));
	return 0;
}
贪心 
#include<bits/stdc++.h>
using namespace std;
const int N = 5e3+5;
int n,m,pre[N],nxt[N];
long long ans,b[N],a[N];
struct A
{
	int id; long long d;
	bool operator < (const A &x) const
	{
		return d>x.d;
	}
};
bool vs[N];
priority_queue<A> q;
int main()
{
	freopen("match.in","r",stdin);
	freopen("match.out","w",stdout);
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
	sort(a+1,a+1+n);
	for(int i=1;i<n;i++) b[i]=a[i+1]-a[i],q.push({i,b[i]}),pre[i]=i-1,nxt[i]=i+1;
	b[0]=b[n]=1e9;
	while(m)
	{
		while(vs[q.top().id]) q.pop();
		int u=q.top().id; long long d=q.top().d; q.pop();
		m--; vs[pre[u]]=vs[nxt[u]]=1; b[u]=b[pre[u]]+b[nxt[u]]-b[u];
		q.push({u,b[u]});
		pre[u]=pre[pre[u]],nxt[u]=nxt[nxt[u]],nxt[pre[u]]=u,pre[nxt[u]]=u;
		ans+=d;
	}
	printf("%lld\n",ans);
	return 0;
}

T2 重定向

大力分讨，不停贪心。

细节处理挂 30pts。

code 
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5+5;
int n,T;
int l,cnt,ans[N],a[N],tot;
bool vs[N];

int main()
{
	freopen("repeat.in","r",stdin);
	freopen("repeat.out","w",stdout);
	scanf("%d",&T);
	while(T--)
	{
		cnt=tot=0;
		set<int> h,p;
		memset(vs,0,sizeof(vs));
		scanf("%d",&n);
		for(int i=1;i<=n;i++)
		{
			scanf("%d",&a[i]); vs[a[i]]=1; 
			if(a[i]!=0) h.insert(a[i]);
		}
		p.insert(100000000);
		for(int i=1;i<=n;i++) if(!vs[i]) p.insert(i);
		bool fl=0; int _1=0;
		for(int i=1;i<=n;i++)
		{
			if(a[i]!=0&&a[i]==_1) continue;
			if(a[i]!=0) h.erase(a[i]);
			
			if(i+1<=n&&fl==0)
			{
				if(a[i]==0)
				{
					if(a[i+1]!=0)
					{
						if(!_1&&!h.empty()&&(*h.begin()<a[i+1])&&(*h.begin()<*p.begin()))
						{
							_1=(*h.begin());
							ans[++tot]=_1;
							fl=1; continue;
						}	
						else if(a[i+1]<*p.begin())
						{
							fl=1; continue;
						}					
						else
						{
							ans[++tot]=*p.begin(); p.erase(p.begin()); continue;
						}
					}
					else 
					{
						if(!_1&&!h.empty()&&*p.begin()>*h.begin())
						{
							_1=(*h.begin());
							ans[++tot]=_1;
							fl=1; continue;							
						}
						else
						{
							ans[++tot]=*p.begin(); p.erase(p.begin()); continue;
						}
					}
				}
				else
				{
					if(a[i+1]!=0&&a[i+1]<a[i]) 
					{
						p.insert(a[i]);
						fl=1; continue;
					}
					else if(a[i+1]==0&&*p.begin()<a[i])
					{
						p.insert(a[i]);
						fl=1; continue;
					}
					else
					{
						ans[++tot]=a[i]; continue;
					}			
				}
			}
			else if(fl==0)
			{
				continue;
			}
			else
			{
				if(a[i]==0) ans[++tot]=*p.begin(), p.erase(p.begin());
				else ans[++tot]=a[i];
			}
		}
		for(int i=1;i<=tot;i++) printf("%d ",ans[i]); putchar('\n');
	}
	return 0;
}

T3 斯坦纳树

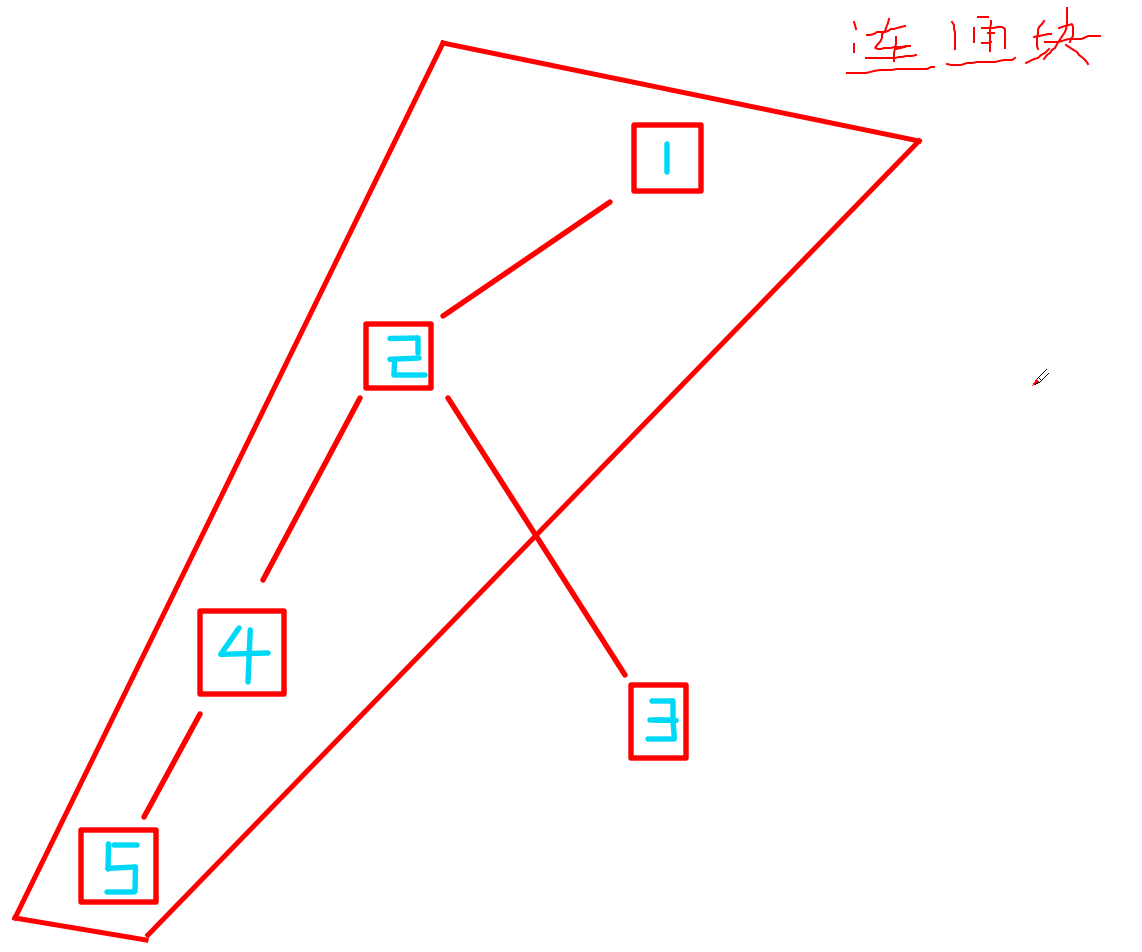
转化题意，发现如果有重边那就是不合法的，考虑什么时候会有重边。

加入的点会形成一个最小连通块，这就是我们要判断的区域。

我们可以将所有点分成三类：

  1. 已经加入的。

  2. 未被加入但在连通块中的。

  3. 不在连通块中的。

考虑一个不在连通块中的点想接入连通块，那么一定会与连通块有一个交点。

假如上图中三号点想加入连通块，那么这个交点就是二号点。

如果二号点已经被加入的话，那么三号点不会造成影响，否则一定会有重边。

所以我们就是想找到这个交点并判断它是否加入。

赛时唐氏做法，线段树维护并查集，每次区间推平维护连通块，单点查询是否是交点，是否选过。

好处就是信息全在线段树里，复杂度能多一个 log 和大常数。

注意每个点最多被铺一遍，所以其实跳父亲的复杂度很低。

最后 O(qlog2(n)) 的复杂度（很松很松）过了。

code 
#include<bits/stdc++.h>
using namespace std;
const int N =3e5+5;
int n,a[N];
int head[N],tot,xx[N],yy[N],zz[N];
struct E {int u,v,w;} e[N<<1];
inline void add(int u,int v,int w) {e[++tot]={head[u],v,w}; head[u]=tot;}
bool fl=1;
int b[N];
inline int find(int x) {return x==b[x]?(x):(b[x]=find(b[x]));}
int sz[N],fa[N][30],dis[N],son[N],dfn[N],dep[N],rk[N],top[N],cnt;

void dfs1(int u,int f)
{
	sz[u]=1; fa[u][0]=f; son[u]=-1; dep[u]=dep[f]+1;
	for(int i=1;i<=20;i++) fa[u][i]=fa[fa[u][i-1]][i-1];
	for(int i=head[u];i;i=e[i].u)
	{
		int v=e[i].v; if(v==f) continue; dis[v]=dis[u]+e[i].w;
		dfs1(v,u); sz[u]+=sz[v];
		if(son[u]==-1||sz[son[u]]<sz[v]) son[u]=v;
	}
}
void dfs2(int u,int t)
{
	top[u]=t; dfn[u]=++cnt; rk[cnt]=u;
	// printf("%d %d\n",u,dfn[u]);
	if(son[u]==-1) return ;
	dfs2(son[u],t);
	for(int i=head[u];i;i=e[i].u)
	{
		int v=e[i].v; if(v==fa[u][0]||v==son[u]) continue;
		dfs2(v,v);
	}
}
namespace SEG
{
	struct T
	{
		int l,r,cnt; bool xu,yo,za,lz;
	} tr[N<<2];
	inline void pushup(int k) {tr[k].cnt=tr[k<<1].cnt+tr[k<<1|1].cnt;}
	inline void pushdown(int k)
	{
		if(tr[k].lz)
		{
			tr[k].lz=0;
			tr[k<<1].lz=1; tr[k<<1].za=1;
			tr[k<<1|1].lz=1; tr[k<<1|1].za=1;
		}
	}
	void bui(int k,int l,int r)
	{
		
		tr[k].l=l; tr[k].r=r;
		if(l>=r) return ; 
		int mid=l+r>>1;
		bui(k<<1,l,mid); bui(k<<1|1,mid+1,r);
	}
	void mdf(int k,int p,int tp)
	{
		if(tr[k].l==tr[k].r)
		{
			if(tp==0)//yo
			{
				if(!tr[k].yo)
				{
					tr[k].cnt-=tr[k].xu; tr[k].yo=1;
				} 				
			}
			else//xu
			{
				if(!tr[k].xu&&!tr[k].yo)
				{
					tr[k].cnt++; tr[k].xu=1;
					// printf("*****\n");
				} 					
			}
			return;
		}
		pushdown(k);
		int mid=tr[k].l+tr[k].r>>1;
		if(p<=mid) mdf(k<<1,p,tp);
		else mdf(k<<1|1,p,tp);
		pushup(k);
	}
	void qmdf(int k,int L,int R)
	{
		if(tr[k].l>=L&&tr[k].r<=R)
		{
			tr[k].za=1; tr[k].lz=1; return;
		}
		pushdown(k);
		int mid=tr[k].l+tr[k].r>>1;
		if(L<=mid) qmdf(k<<1,L,R);
		if(R>mid) qmdf(k<<1|1,L,R);
		pushup(k);
	}
	bool que(int k,int p)
	{
		if(tr[k].l==tr[k].r) return tr[k].za;
		pushdown(k);
		int mid=tr[k].l+tr[k].r>>1;
		if(p<=mid) return que(k<<1,p);
		else return que(k<<1|1,p);
	}
} using namespace SEG;

void mdfpath(int x,int y)
{
	while(top[x]!=top[y])
	{
		if(dep[top[x]]<dep[top[y]]) swap(x,y);
		qmdf(1,dfn[top[x]],dfn[x]);
		x=fa[top[x]][0];
		
	}
	if(dfn[x]>dfn[y]) swap(x,y);
	qmdf(1,dfn[x],dfn[y]);
	return;
}

void change(int x)
{
	int tmp=x;
	mdf(1,dfn[x],0);
	if(que(1,dfn[x])) return;
	for(int i=20;i>=0;i--)
	{
		if(!fa[x][i]) continue;
		if(que(1,dfn[fa[x][i]])) continue;
		else x=fa[x][i];
	}
	mdf(1,dfn[fa[x][0]],1);
	mdfpath(fa[x][0],tmp);
}

int main()
{
	freopen("tree.in","r",stdin);
	freopen("tree.out","w",stdout);
	scanf("%d",&n);
	for(int i=1;i<=n;i++) b[i]=i;
	for(int i=1;i<n;i++)
	{
		int x,y,z; scanf("%d%d%d",&x,&y,&z);
		x=find(x); y=find(y);
		if(z==0) b[x]=y; 
		xx[i]=x; yy[i]=y; zz[i]=z;
	}
	for(int i=1;i<n;i++)
	{
		if(zz[i]!=0) 
		{
			int x=find(xx[i]),y=find(yy[i]);
			add(x,y,zz[i]); add(y,x,zz[i]);
		}
	}
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	dfs1(find(a[1]),0);
	dfs2(find(a[1]),find(a[1]));
	bui(1,1,n);
	int v=dfn[find(a[1])];
	mdf(1,v,0); 
	qmdf(1,v,v); 
	printf("1");
	for(int i=2;i<=n;i++)
	{
		v=find(a[i]); 
		change(v);
		if(tr[1].cnt==0) printf("1");
		else printf("0");
	}
	return 0;
}

T4 直径

咕咕咕

posted @   ppllxx_9G  阅读(26)  评论(2)  编辑  收藏  举报
相关博文：
·  2024.9.27 模拟赛 CSP5
·  2024.9.24 模拟赛 CSP4
·  51nod模拟4/CSP-S模拟3
·  [总结]模拟赛2022/1/19
·  CSP集训题解
阅读排行：
· 25岁的心里话
· 闲置电脑爆改个人服务器（超详细） #公网映射 #Vmware虚拟网络编辑器
· 零经验选手，Compose 一天开发一款小游戏！
· 因为Apifox不支持离线，我果断选择了Apipost！
· 通过 API 将Deepseek响应流式内容输出到前端
点击右上角即可分享
微信分享提示
AI IDE Trae