2024.9.27 模拟赛 CSP5
模拟赛
无
T1 光
贪心,发现首先让最大的减 \(4\),这样最优并且不会涉及向下取整,等到数据范围小了以后直接 \(O(n^4)\) 暴力枚举。
code
#include<bits/stdc++.h>
using namespace std;
int a,b,c,d;
int ans=1e9;
#define mx(x,y) (x>y?(x):(y))
#define mi(x,y) (x<y?(x):(y))
int main()
{
freopen("light.in","r",stdin);
freopen("light.out","w",stdout);
scanf("%d%d%d%d",&a,&b,&c,&d);
int ans=0;
while(a>4||b>4||c>4||d>4)
{
int x=mx(a,mx(b,mx(c,d)));
ans+=4;
if(x==a) a-=4, b-=2, c-=2, d-=1;
else if(x==b) b-=4, a-=2, d-=2, c-=1;
else if(x==c) c-=4, a-=2, d-=2, b-=1;
else if(x==d) d-=4, b-=2, c-=2, a-=1;
}
a=mx(a,0); b=mx(b,0); c=mx(c,0); d=mx(d,0);
int tmp=1e9;
for(int x=0;x<=a;x++)
for(int y=0;y<=b;y++)
for(int z=0;z<=c;z++)
{
int w=mx((a-x-(y>>1)-(z>>1))<<2,mx(mx(d-(x>>2)-(y>>1)-(z>>1),(c-z-(x>>1)-(y>>2))<<1),(b-y-(x>>1)-(z>>2))<<1));
if(w<0) w=0;
tmp=mi(tmp,x+y+z+w);
}
ans+=tmp;
printf("%d\n",ans);
return 0;
}
T2 爬
trick,按位考虑,如果爬完某个点上有奇数个蚂蚁这一位为一,那么就会有贡献。
先考虑第 \(i\) 位,点 \(u\)(\(u!=1\)),它的儿子中有 \(cnt\) 个儿子第 \(i\) 位为一。
发现这个点是否产生贡献只与自己和儿子是否跳有关,不妨直接让 \(cnt\) 表示包括自己在内,第 \(i\) 位为一的点的个数。
奇数个在这个点上的方案数就是:
\[\binom{cnt}{1}+\binom{cnt}{3}+\binom{cnt}{5}+\dots=2^{cnt-1}
\]
在加上那些无关儿子任选的方案,减去只有一个点的方案,最后乘上其他点乱跳的方案,注意特判 \(1\) 号点不能向上跳。
化简后差不多都是 \(2\) 的次幂的形式,注意如果 \(cnt \lt 1\)、\(cnt \lt 2\) 的情况都要特判,因为组合数化简前无意义,不能正常化简。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 1e5+5,mod = 1e9+7;
int n,a[N];
vector<int> g[N];
LL _2[N],tmp,ans;
void dfs(int u,int m)
{
for(int v:g[u]) dfs(v,m);
int cnt=(a[u]>>m)&1,sz=1;
for(int v:g[u]) cnt+=((a[v]>>m)&1),sz++;
if(cnt==0||sz==1) return;
if(u==1)
{
if(((a[u]>>m)&1)&&cnt>=2) tmp=(tmp+(_2[sz-2]+mod-1)%mod*_2[n-sz]%mod)%mod;
else if(((a[u]>>m)&1)) tmp=(tmp+(_2[sz-1]+mod-1)%mod*_2[n-sz]%mod)%mod;
else if(!((a[u]>>m)&1)) tmp=(tmp+_2[n-2]%mod)%mod;
}
else tmp=(tmp+(_2[sz-1]+mod-cnt)%mod*_2[n-sz-1]%mod)%mod;
}
int main()
{
freopen("climb.in","r",stdin);
freopen("climb.out","w",stdout);
scanf("%d",&n);
_2[0]=1; for(int i=1;i<=max(n,30);i++) _2[i]=(_2[i-1]<<1)%mod;
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=2;i<=n;i++) {int x; scanf("%d",&x); g[x].push_back(i);}
for(int i=0;i<=30;i++) {tmp=0; dfs(1,i); ans=(ans+_2[i]*tmp%mod)%mod;}
printf("%lld\n",ans);
return 0;
}
T3 字符串
T3 放贪心…………
正解不是 DP,直接贪心。
想要吃 A、B 交替的的贡献,于是每 \(c\) 个 B 放一个 A,枚举交替放了多少组(必须枚举,不能贪心)。
然后剩下的每 \(a\) 个 A 有一个贡献,B 先补满,然后每 \(b\) 个 B 有一个贡献。
code
#include<bits/stdc++.h>
using namespace std;
int T,a,b,c,N,M;
int main()
{
freopen("string.in","r",stdin);
freopen("string.out","w",stdout);
scanf("%d",&T);
while(T--)
{
int ans=0;
scanf("%d%d%d%d%d",&N,&M,&a,&b,&c);
for(int i=0;i<=min(N,M/c);i++)
{
int k=i,sum=0,n=N,m=M;
n-=k; m-=k*c; sum+=k*2;
if(n) n--,sum++; if(m) m--,sum++;
sum+=n/a;
sum+=((c-1)/b)*k;
int tmp=b-(c%b)+1; if(c%b==0) tmp=1;
while(k&&m-tmp>=0) m-=tmp,sum++,k--;
sum+=m/b;
ans=max(ans,sum);
}
printf("%d\n",ans);
}
return 0;
}
T4 奇怪的函数
首先容易想到,对于每一段,答案都是一个关于 \(x\) 的分段函数,分三段。
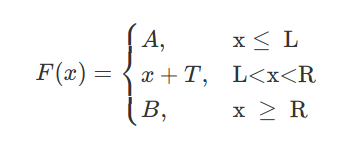
所以考虑分块或线段树维护分段函数。
(懒了)
code
#include<bits/stdc++.h>
using namespace std;
const int N = 3e5+5;
int n,m,B,cnt,bl[N],s[1000],e[1000],l[1000],r[1000],rs[1000],pre[1000];
struct OP {int c,v;} op[N];
inline int f(int p)
{
int res=0;
for(int i=s[p];i<=e[p];i++)
op[i].c==1?(res+=op[i].v):(op[i].c==2?(res=min(res,op[i].v)):(res=max(res,op[i].v)));
return res;
}
int main()
{
freopen("function.in","r",stdin);
freopen("function.out","w",stdout);
scanf("%d",&n); B=sqrt(n); cnt=n/B;
for(int i=1;i<=n;i++) scanf("%d%d",&op[i].c,&op[i].v);
for(int i=1;i<=cnt;i++)
{
s[i]=e[i-1]+1; e[i]=e[i-1]+B; e[cnt]=n;
pre[i]=0; l[i]=0; r[i]=1e9;
for(int j=s[i];j<=e[i];j++)
{
bl[j]=i;
if(op[j].c==1) pre[i]+=op[j].v;
else if(op[j].c==2) r[i]=min(r[i],op[j].v-pre[i]);
else if(op[j].c==3) l[i]=max(l[i],op[j].v-pre[i]);
}
rs[i]=f(i);
}
scanf("%d",&m);
while(m--)
{
int c,x,y; scanf("%d",&c);
if(c==4)
{
scanf("%d",&x);
for(int i=1;i<=cnt;i++)
{
if(l[i]<r[i])
{
if(x<l[i]) x=l[i];
else if(x>r[i]) x=r[i];
x+=pre[i];
}
else x=rs[i];
}
printf("%d\n",x);
}
else
{
scanf("%d%d",&x,&y);
op[x].c=c; op[x].v=y;
int p=bl[x]; pre[p]=0; l[p]=0; r[p]=1e9;
for(int j=s[p];j<=e[p];j++)
{
if(op[j].c==1) pre[p]+=op[j].v;
else if(op[j].c==2) r[p]=min(r[p],op[j].v-pre[p]);
else if(op[j].c==3) l[p]=max(l[p],op[j].v-pre[p]);
}
rs[p]=f(p);
}
}
return 0;
}


