2024.9.23 模拟赛 CSP 3
模拟赛
数据出锅 \(\times n\),题面出锅 \(\times n\)。
出题人的心思全放在对 \(\mathbb{CCF}\) 的热爱上了。
T1 奇观
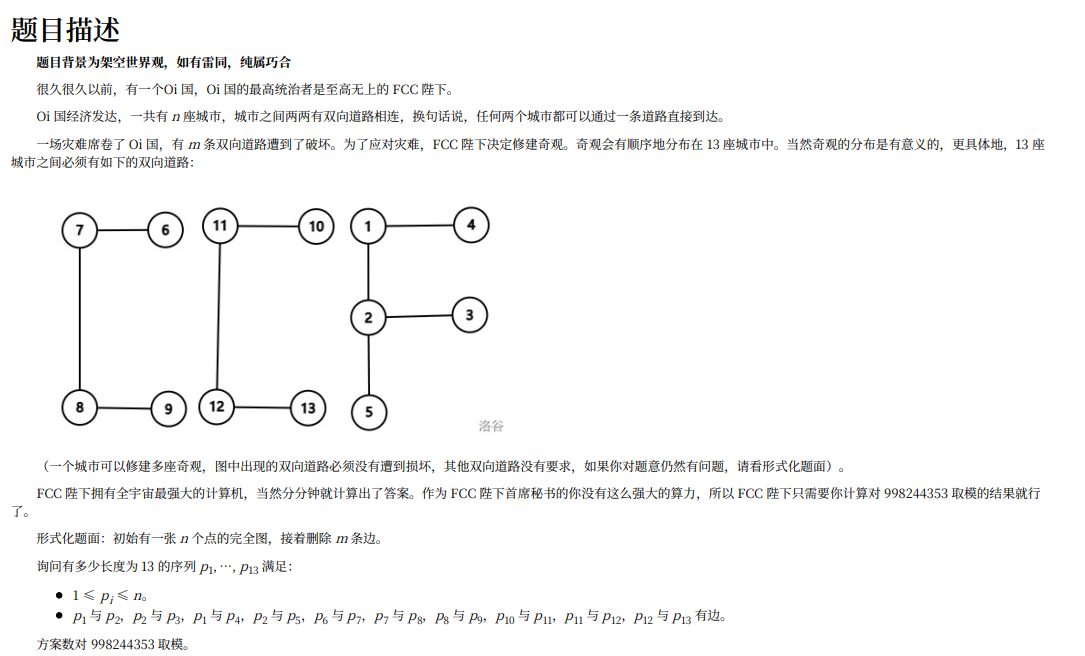
容易发现 C C F 是独立的,分别统计就行。。
第一想法是搜,赛时只拿 \(55pts\),好像能拿更高。
题解给了一种比较巧妙的方法。发现 F 可以看成三段,两段长度为 \(2\)的,一段长度为 \(3\) 的,显然 \(C\) 也可以用两段表示。
所以考虑令 \(v1_i\) 表示以 \(i\) 为起点长度为 \(2\) 的序列,\(v2_i\) 表示以 \(i\) 为起点长度为 \(3\) 的序列。
但是边数很多,但发现 \(m\) 较小,所以考虑容斥,\(v1_i\) 初始都是 \(n-1\),每删一条以 \(i\) 为起点的的边就减一。
更新完 \(v1\) 统计一个和,\(v2_i\) 就用这个和减去对应的边的 \(v1\) 就行。

code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 1e5+5,mod = 998244353;
int n,m;
vector<int> v[N];
LL v1[N],v2[N];
int main()
{
freopen("a.in","r",stdin);
freopen("a.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) v1[i]=n-1;
for(int i=1;i<=m;i++)
{
int x,y; scanf("%d%d",&x,&y);
v[x].push_back(y); v[y].push_back(x);
}
LL sum=0;
for(int i=1;i<=n;i++) v1[i]-=v[i].size(),sum+=v1[i];
for(int i=1;i<=n;i++)
{
v2[i]=sum-v1[i];
for(int j:v[i]) v2[i]-=v1[j];
}
LL C=0,F=0;
for(int i=1;i<=n;i++) C=(C+1ll*v1[i]*v2[i])%mod,F=(F+1ll*v1[i]*v1[i]%mod*v2[i])%mod;
printf("%lld\n",C*C%mod*F%mod);
return 0;
}
T2 铁路

赛时切了还挺爽。虽然比较麻烦。
首先发现加新点的操作很麻烦,不如每次直接合并到两点的 lca 中,至于编号的改变映射过去就行。
然后发现需要用并查集维护,并且会把一条路径上的点的祖先都推平为一个点,考虑用线段树维护父亲,进行区间推平。
每次找到深度最浅的父亲(注意这里),其实类似暴跳。但是每条边只会被合并一次,所以复杂度正确。
最后统计答案,直接在线段树维护 \(fa_x=x\) 的个数就好了,也就是修改时判断一下当前新的父亲是否在这个区间里,如果在,就有 \(1\) 的贡献,否则没有。
注意 dfn 序和点编号的关系。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5+5;
int n,m;
int head[N],tot;
int bl[N];
struct E {int u,v;} e[N<<1];
inline void add(int u,int v) {e[++tot]={head[u],v}; head[u]=tot;}
int ys[N];
int sz[N],son[N],top[N],dfn[N],rk[N],fa[N],cnt,dep[N];
inline void dfs1(int u,int f)
{
sz[u]=1; dep[u]=dep[f]+1; fa[u]=f; son[u]=-1;
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v; if(v==f) continue;
dfs1(v,u); sz[u]+=sz[v];
if(son[u]==-1||sz[son[u]]<sz[v]) son[u]=v;
}
}
inline void dfs2(int u,int t)
{
top[u]=t; dfn[u]=++cnt; rk[cnt]=u;
if(son[u]==-1) return;
dfs2(son[u],t);
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v; if(v==fa[u]||v==son[u]) continue;
dfs2(v,v);
}
}
int lca(int x,int y)
{
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]]) swap(x,y);
x=fa[top[x]];
}
if(dep[y]<dep[x]) swap(x,y);
return x;
}
namespace SEG
{
struct T {int l,r,bl,lz,sum;} tr[N<<2];
inline void pushdown(int k)
{
if(tr[k].lz)
{
int lz=tr[k].lz; tr[k].lz=0;
tr[k<<1].lz=lz; tr[k<<1].bl=lz;
tr[k<<1|1].lz=lz; tr[k<<1|1].bl=lz;
if(lz>=tr[k<<1].l&&lz<=tr[k<<1].r) tr[k<<1].sum=1;
else tr[k<<1].sum=0;
if(lz>=tr[k<<1|1].l&&lz<=tr[k<<1|1].r) tr[k<<1|1].sum=1;
else tr[k<<1|1].sum=0;
}
}
inline void pushup(int k) {tr[k].sum=tr[k<<1].sum+tr[k<<1|1].sum;}
inline void bui(int k,int l,int r)
{
tr[k].l=l; tr[k].r=r;
if(l==r) return tr[k].bl=l,tr[k].sum=1,void(0);
int mid=l+r>>1;
bui(k<<1,l,mid); bui(k<<1|1,mid+1,r);
pushup(k);
}
inline void mdf(int k,int l,int r,int v)
{
if(l<=tr[k].l&&r>=tr[k].r)
{
if(v>=tr[k].l&&tr[k].r>=v) tr[k].sum=1;
else tr[k].sum=0;
tr[k].bl=v; tr[k].lz=v; return;
}
pushdown(k);
int mid=tr[k].l+tr[k].r>>1;
if(l<=mid) mdf(k<<1,l,r,v);
if(r>mid) mdf(k<<1|1,l,r,v);
pushup(k);
}
inline int que(int k,int p)
{
if(tr[k].l==tr[k].r)
{
return tr[k].bl;
}
pushdown(k);
int mid=tr[k].l+tr[k].r>>1;
if(p<=mid) return que(k<<1,p);
else return que(k<<1|1,p);
}
} using namespace SEG;
void mdfpath(int x,int y,int v)
{
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]]) swap(x,y);
mdf(1,dfn[top[x]],dfn[x],v);
x=fa[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
mdf(1,dfn[x],dfn[y],v);
}
int find(int x)
{
int tmp=que(1,dfn[x]);
if(tmp==dfn[x]) return x;
else return find(rk[tmp]);
}
int main()
{
freopen("a.in","r",stdin);
freopen("a.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<n;i++)
{
int x,y; scanf("%d%d",&x,&y);
add(x,y); add(y,x);
}
dfs1(1,0); dfs2(1,1); bui(1,1,n);
for(int i=1;i<=m;i++)
{
int x,y; scanf("%d%d",&x,&y);
if(x>n) x=ys[x-n]; if(y>n) y=ys[y-n];
int l=find(lca(x,y)); ys[i]=l;
mdfpath(x,y,dfn[l]);
printf("%d\n",tr[1].sum);
}
return 0;
}
T3 光纤

学习计算几何。
狂补文化课???
结论是维护凸包,旋转卡壳板子。
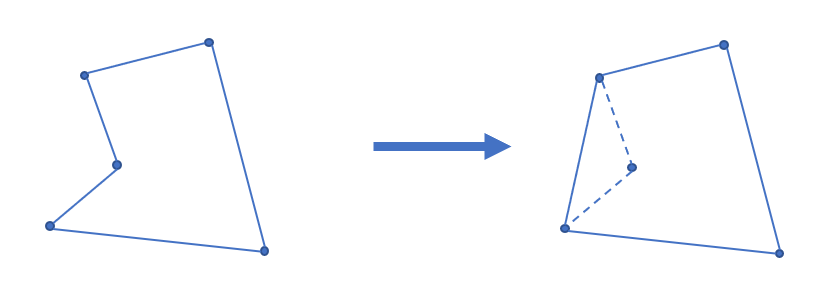
凸包
先学习维护凸包 板子。
凸包就是能包含平面上所有点的最小凸多边形,可以理解成用一个橡皮筋把所有点圈住的图形。
我们按横坐标为第一关键字,纵坐标为第二关键字从小到大排序。显然第一个点——也就是最左下方的点一定在凸包上。
于是我们从这个点开始逆时针求凸包,由于要建立凸多边形,所以一定是一直“左拐”,如果出现了“右拐”,那么说明这个点不在凸包上。
容易想到用单调栈的方法维护,问题是怎么判断当前是“左拐”还是“右拐”。
引入新知识(其实不算新)——外积(也叫叉积)。oi-wiki上有介绍,也可以去看数学课本。
根据右手法则如果 \(\bm{a} \times \bm{b}\) 中,\(\bm{b}\) 在 \(\bm{a}\) 的逆时针方向,那么外积向上(为正)。而两个向量的外积可以用 \(x0 \times y1 - y0 \times x1\) 计算(这里建议直接看行列式理解)。
因此可以通过比较外积的正负来进行判断(外积求法向量也很方便哦)。
分别正序、逆序跑一遍,维护出上凸壳和下凸壳。
code(凸包周长)
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+5;
int n;
struct node {double x,y;} p[N];
inline double operator * (const node &x,const node &y) {return x.x*y.y-x.y*y.x;}
inline node operator - (const node &x,const node &y) {return {y.x-x.x,y.y-x.y};}
inline double dis(const node &x,const node &y) {return sqrtl((y.x-x.x)*(y.x-x.x)+(y.y-x.y)*(y.y-x.y));}
int st[N],tp;
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
double x,y; scanf("%lf%lf",&x,&y);
p[i]={x,y};
}
sort(p+1,p+1+n,[&](const node &x,const node &y) {return x.x==y.x?(x.y<y.y):(x.x<y.x);});
st[++tp]=1;
for(int i=2;i<=n;i++)
{
while(tp>=2&&(p[st[tp]]-p[st[tp-1]])*(p[i]-p[st[tp]])<=0) tp--;
st[++tp]=i;
}
int lim=tp;
for(int i=n-1;i>=1;i--)
{
while(tp>lim&&(p[st[tp]]-p[st[tp-1]])*(p[i]-p[st[tp]])<=0) tp--;
st[++tp]=i;
}
double ans=0;
for(int i=1;i<tp;i++) ans+=dis(p[st[i]],p[st[i+1]]);
printf("%.2lf\n",ans);
return 0;
}
旋转卡壳
最原始的作用是求凸包的直径,思想很简单,旋转枚举每个点,同时维护到这个点最远的点,因为都是逆时针转,所以双指针指一下就行了。
这里就是比较两点间的距离,也可以换成点线距等等,思想就是这样。旋转卡壳
code(凸包直径)
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5+5;
int n;
struct node {double x,y;} p[N];
int st[N],tp;
inline double operator * (const node &x,const node &y) {return x.x*y.y-x.y*y.x;}
inline node operator - (const node &x,const node &y) {return {y.x-x.x,y.y-x.y};}
inline double dis2(node x,node y) {return sqrt((x.x-y.x)*(x.x-y.x)+(x.y-y.y)*(x.y-y.y));}
inline double cal(node x,node y,node z) {return abs((y-x)*(z-y));}
double get()
{
int j=4;
if(tp<=3) return dis2(p[st[1]],p[st[2]]);
double res=0;
for(int i=1;i<tp;i++)
{
while(cal(p[st[i]],p[st[i+1]],p[st[j]])<=cal(p[st[i]],p[st[i+1]],p[st[j%tp+1]])) j=j%tp+1;
res=max(res,max(dis2(p[st[i+1]],p[st[j]]),dis2(p[st[i]],p[st[j]])));
}
return res;
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
double x,y; scanf("%lf%lf",&x,&y);
p[i]={x,y};
}
sort(p+1,p+1+n,[&](const node &x,const node &y){return x.x==y.x?(x.y<y.y):(x.x<y.x);});
st[++tp]=1;
for(int i=2;i<=n;i++)
{
while(tp>1&&(p[st[tp]]-p[st[tp-1]])*(p[i]-p[st[tp]])<=0) tp--;
st[++tp]=i;
}
int tmp=tp;
for(int i=n-1;i>=1;i--)
{
while(tp>tmp&&(p[st[tp]]-p[st[tp-1]])*(p[i]-p[st[tp]])<=0) tp--;
st[++tp]=i;
}
printf("%.6lf\n",get());
return 0;
}
本题
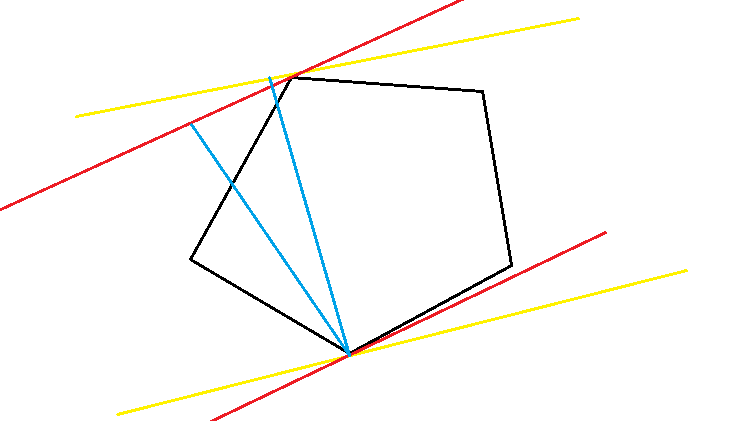
转化问题,维护凸包,问题就是用一对平行线“夹住”凸包,使平行线之间距离最短。
首先得到结论,直线一定平行于凸包的一条边时最优。由上图可知,当一条直线向凸包的一条边方向旋转后,距离变小了(具体往哪个方向转好像和原本垂足的位置有关,但不重要)。
所以推断最终一定取到和某一条边平行时最优。
然后直接旋转卡壳就完了,判断的依据从点点距变成点线距。
补充公式:
点点距:\(\sqrt{\Delta x^2+\Delta y^2}\)
点线距:\(\dfrac{Ax+By+C}{\sqrt{A^2+B^2}}\)
已知两点求直线:\(-\Delta y x+\Delta x y+x0y1-x1y0=0\)(\(-\Delta y x+\Delta x y+a \times b=0\))
平行线距离:\(\dfrac{C0-C1}{\sqrt{A^2+B^2}}\)
code
#include<bits/stdc++.h>
using namespace std;
#define LL __int128
const int N = 1e6+5;
const long double inf=1e-9;
int n;
struct ND {int x,y;} p[N],a[N];
struct P {LL fz=0,fm=0; long double d=0;};
int st[N],tp;
#define esp(x,y) (x-y<inf)
#define mi(x,y) (x.d-y.d<inf?(x):(y))
inline void write(LL x) {return x?(write(x/10),putchar((x%10)|48)),void(0):(void(0));}
inline LL operator * (const ND &x,const ND &y) {return (LL)x.x*y.y-(LL)x.y*y.x;}
inline ND operator - (const ND &x,const ND &y) {return {y.x-x.x,y.y-x.y};}
inline LL gcd(LL x,LL y) {return (!y)?(x):(gcd(y,x%y));}
inline P dis(ND x0,ND x1,ND y)
{
LL yy=x0.y-x1.y,xx=x1.x-x0.x,c=x0*x1;
LL fz=yy*y.x+xx*y.y+c,fm=(yy*yy+xx*xx)*4; fz=fz*fz;
LL g=gcd(fz,fm); fz/=g; fm/=g;
return {fz,fm,(long double)fz/fm};
}
int main()
{
freopen("a.in","r",stdin);
freopen("a.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
int x,y; scanf("%d%d",&x,&y); p[i]={x,y};
}
sort(p+1,p+1+n,[&](const ND &x,const ND &y){return x.x==y.x?(x.y<y.y):(x.x<y.x);});
st[++tp]=1;
for(int i=2;i<=n;i++)
{
while(tp>1&&(p[st[tp]]-p[st[tp-1]])*(p[i]-p[st[tp]])<=0) tp--;
st[++tp]=i;
}
int tmp=tp;
for(int i=n-1;i>=1;i--)
{
while(tp>tmp&&(p[st[tp]]-p[st[tp-1]])*(p[i]-p[st[tp]])<=0) tp--;
st[++tp]=i;
}
for(int i=1;i<=tp;i++) a[i]=p[st[i]];
if(tp<=3) printf("%d/%d\n",0,1);
else
{
P ans;
int j=3;
for(int i=2;i<=tp;i++)
{
while(esp(dis(a[i],a[i-1],a[j]).d,dis(a[i],a[i-1],a[j%tp+1]).d)) j=j%tp+1;
if(ans.d==0) ans=dis(a[i],a[i-1],a[j]);
else ans=mi(ans,dis(a[i],a[i-1],a[j]));
}
write(ans.fz); putchar('/'); write(ans.fm);
}
}
T4 权值 (咕咕咕。。。)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号