小集训
小集训
改题倒是改的勤了，但是懒得写博客了。。。
Day 1
T1 喜剧的迷人之处在于
在于啥？？？
先把所有平方数筛出来，然后对于 \(a\)，首先把它里面的平方数提出来，剩下 \(x\)，\(b\) 一定包含 \(x\) 和另一个平方数，可以二分（暴力也可以）。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
#define mx(x,y) (x>y?x:y)
const int N = 1e6;
int t; LL p[N+1];
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&t);
for(LL i=1;i<=N;i++) p[i]=i*i;
while(t--)
{
LL a,l,r,tmp=1; scanf("%lld%lld%lld",&a,&l,&r);
for(int i=2;i<=N&&p[i]<=a;i++)
{
while(a%p[i]==0) a/=p[i],tmp*=p[i];
}
bool fl=0;
for(int i=mx(sqrt(l/a)-1,1);i<=N;i++)
{
LL tmp1=a*p[i];
if(tmp1>=l&&tmp1<=r)
{
printf("%lld\n",tmp1); fl=1; break;
}
if(tmp1>r) break;
}
if(!fl) printf("-1\n");
}
return 0;
}
T2 镜中的野兽
\(lcm\) 一定是 \(gcd\) 的倍数，容易想到枚举 \(gcd\)。
确定 \(gcd\) 后就可以把每个元素都除以 \(gcd\)，令 \(x=lcm/gcd\)（都还好想）。
我们试着列一下式子：
接下来有两种考虑方式：
莫反
试着将这个式子转化为熟悉的莫反形式。发现不太行。。。
考虑莫反的定义：
我们想要构造一个类似的函数，也就是出现 \(\sum_{d \mid x}\)，于是就出现了一下两个函数：
这两个神奇的函数具有以下性质：
如果不知道上面为什么，请看这里 （不会真的有人需要看吧）
显然我们可以用莫反搞，但如何求 \(h(x)\) 呢？
其实我们设计这的两个函数使我们要求的限制变松了，\(f(x)\) 要使 \(gcd=1 \land lcm=x\)，是恰好等于。
而 \(h(x)\) 只需满足 \(gcd \mid x \land lcm \mid x\)，其实这就是在 x 的因数里面任选 n 个不同的数，所以 \(h(x)=\dbinom{d(x)}{n}\)。
总结一下：
注意记忆化，远远卡不到上界。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 1e5+5;
int n,m,mod,fac[N],inv[N],ans;
unordered_map<int,int> f,g,dd,mu;
inline void init()
{
fac[0]=inv[0]=inv[1]=fac[1]=1;
for(int i=2;i<N;i++) fac[i]=1ll*fac[i-1]*i%mod,inv[i]=1ll*(mod-mod/i)*inv[mod%i]%mod;
for(int i=2;i<N;i++) inv[i]=1ll*inv[i-1]*inv[i]%mod;
}
inline int C(int n,int m)
{
if(n<m) return 0;
return 1ll*fac[n]*inv[m]%mod*inv[n-m]%mod;
}
inline int getmu(int x)
{
if(mu.find(x)!=mu.end()) return mu[x];
int tmp=sqrt(x),op=x,res=0;
for(int i=2;i<=tmp;i++)
{
if(!(x%i))
{
x/=i;
if(!(x%i)) return mu[op]=0;
res++;
}
}
if(x>1) res++;
return mu[op]=(res&1)?(mod-1):(1);
}
inline int D(int k)
{
if(k==0) return 0;
if(dd.find(k)!=dd.end()) return dd[k];
int tmp=sqrt(k),res=0;
for(int i=1;i<=tmp;i++)
{
if(!(k%i))
{
res++;
if(i*i!=k) res++;
}
}
return dd[k]=res;
}
inline int G(int d)
{
if(d==0) return 0;
if(g.find(d)!=g.end()) return g[d];
int tmp=sqrt(d),res=0;
for(int k=1;k<=tmp;k++)
{
if(!(d%k))
{
int t=d/k;
res=(res+1ll*getmu(k)*C(D(t),n))%mod;
if(t!=k) res=(res+1ll*getmu(t)*C(D(k),n))%mod;
}
}
return g[d]=res;
}
inline int F(int x)
{
// if(x==0) return 1;
if(f.find(x)!=f.end()) return f[x];
int tmp=sqrt(x),res=0;
for(int d=1;d<=tmp;d++)
{
if(!(x%d))
{
int t=x/d;
res=(res+1ll*getmu(d)*G(t))%mod;
if(t!=d) res=(res+1ll*getmu(t)*G(d))%mod;
}
}
return f[x]=res;
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d%d",&n,&m,&mod); int tmp=sqrt(m);
init();
for(int x=1;x<=tmp;x++)
{
if(!(m%x))
{
ans=(1ll*ans+F(x-1))%mod;
if(x*x!=m) ans=(1ll*ans+F(m/x-1))%mod;;
}
}
printf("%d\n",ans);
return 0;
}
容斥
我们设 \(x=\prod p_i^{c_i}\)，为了使 \(lcm=x \land gcd=1\)，必须有一项不含因数 \(p_i\)，并且有一项包含因数 \(p_i^{c_i}\)。
单独考虑一个质因子，我们想要的答案是既卡了上界又卡了下界的方案数，因为有两个限制条件所以不太好求。
在这里进行容斥，我们可以由 卡上界、卡下界、都不卡 的情况得到答案（画个 VN 图看看）。
然后推广到多个质因子的情况，我们可以将卡不卡 上/下 界作为状态，枚举所有状态进行容斥（这里的容斥系数是 \((-1)^{popcount(S)}\)，也就是卡了奇数个限制）。
如果没有限制那么每个质因数有 \(k_i+1\) 种方案，减去钦定的卡上下界的再相乘一共有多少种因子可以选，答案就是选 \(n\) 个的方案数。
最后你会发现莫反就是一种容斥。
%%%K8 的题解
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 1e5+5;
int n,m,mod,fac[N],inv[N],ans,p[N];
bool vs[N];
inline void init()
{
fac[0]=inv[0]=inv[1]=fac[1]=1;
for(int i=2;i<N;i++) fac[i]=1ll*fac[i-1]*i%mod,inv[i]=1ll*(mod-mod/i)*inv[mod%i]%mod;
for(int i=2;i<N;i++)
{
inv[i]=1ll*inv[i-1]*inv[i]%mod;
if(!vs[i]) p[++p[0]]=i;
for(int j=1;j<=p[0]&&i*p[j]<N;j++)
{
vs[i*p[j]]=1;
if(!(i%p[j])) break;
}
}
}
inline int C(int n,int m)
{
if(n<m) return 0;
return 1ll*fac[n]*inv[m]%mod*inv[n-m]%mod;
}
inline int F(int x)
{
int tmp=x,res=0;
vector<int> k;
for(int i=1;i<=p[0]&&p[i]*p[i]<=tmp;i++)
{
if(!(tmp%p[i]))
{
k.push_back(0);
while(!(tmp%p[i])) tmp/=p[i],k.back()++;
}
if(tmp==1) break;
}
if(tmp>1) k.push_back(1);
int l=k.size(),top=(1<<(l<<1))-1;
for(int s=0;s<=top;s++)
{
int y=1;
for(int i=0;i<l;i++)
{
int k8=k[i]-((s>>i)&1)-((s>>i+l)&1)+1;
if(k8<=0) {y=0; break;}
else y*=k8;
}
int k5=__builtin_popcount(s);
(k5&1)?(res=(1ll*res-C(y,n)+mod)%mod):(res=(1ll*res+C(y,n))%mod);
if(!s&&y<n) return 0;
}
return res;
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d%d",&n,&m,&mod); int tmp=sqrt(m);
init();
for(int x=1;x<=tmp;x++)
{
if(!(m%x))
{
ans=(1ll*ans+F(x-1))%mod;
if(x*x!=m) ans=(1ll*ans+F(m/x-1))%mod;;
}
}
printf("%d\n",ans);
return 0;
}
我愿相信你所描述的童话
咕咕咕。。。
先放个暴力。
和最长上升子序列差不多，发现值域很小，所以将原来用下标做状态改为权值做状态。
先正着跑一遍，然后倒着跑一遍好像就做完了。
然后你发现连大样例都过不去。。。
发现如果存在相等的数，那么它作为顶点时会有重复的贡献，所以要去掉这一部分贡献。
只有在做顶点时贡献会重算，而不会影响正常递推过程，所以考虑多开一个数组，单独记录没有重复值时的答案（也就是不用自己更新自己）。
正着跑的时候维护这个数组，倒着就正常，最后用没有重复部分的更新答案。
然后暴力就写完了，正解考虑二进制，将前后 \(\frac{m}{2}\) 分别考虑，平衡修改和查询的复杂度。（还没改）
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
#define MOD(x) (x>mod?x-mod:x)
const int N = 3e5+5,mod = 1e9+7;
int n,f[1<<20],g[1<<20],k[N],m,ans;
LL s[N];
inline LL read()
{
LL res=0; char x=getchar();
while(x>'9'||x<'0') x=getchar();
while(x>='0'&&x<='9') res=(res<<1)+(res<<3)+(x^48),x=getchar();
return res;
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) s[i]=read();
for(int i=1;i<=n;i++)
{
int j=0; k[i]=1;
while(j<s[i])
{
if((s[i]|j)==s[i]) k[i]=MOD(1ll*k[i]+f[j]),j++;
else j+=(j&-j);
}
f[s[i]]=MOD(MOD(1ll*f[s[i]]+f[s[i]]+k[i]));//k 表示不算重值的位置贡献，f 由原来的表示重值的贡献，更新后表示此时这个值的贡献。
}
for(int i=n;i>=1;i--)
{
int j=0,tmp=1;//tmp 表示此位置的贡献，g 表示这个值的贡献，统计位置的贡献。
while(j<=s[i])
{
if((s[i]|j)==s[i]) tmp=MOD(1ll*tmp+g[j]),j++;
else j+=(j&-j);
}
g[s[i]]=MOD(1ll*g[s[i]]+tmp);
ans=MOD(ans+1ll*tmp*k[i]%mod);
}
printf("%d\n",ans);
return 0;
}
Baby Doll
科技科技科技。。。
Day 2
T1 不相邻集合
赛时好多假做法都过了，包括我的。
想到值域上 dp，但是发现有后效性，莫名加了个判断单调性的就过了，数据纯随机的锅。
其实问题就是求值域上最长不连续的序列，每次会加入一个数。
对于值域上每一个连续的段，长度为 \(len\)，显然能选出长度为 \(\lceil \frac{len}{2} \rceil\) 的不连续子序列，所以只需要记录连续的段就可以。
可以并查集维护，但是直接用数组，把每一段的左右端点互相对应一下就行。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 3e5+5,M = 5e5+5;
int n,a[N],pre[M],nxt[M],ans;
bool vs[M];
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]),pre[a[i]]=nxt[a[i]]=a[i];
for(int i=1;i<=n;i++)
{
if(vs[a[i]]) printf("%d ",ans);
else
{
if(vs[a[i]-1]&&vs[a[i]+1])
{
ans-=(a[i]-1-pre[a[i]-1]+1+1)>>1;
ans-=(nxt[a[i]+1]-a[i]-1+1+1)>>1;
pre[nxt[a[i]+1]]=pre[a[i]-1];
nxt[pre[a[i]-1]]=nxt[a[i]+1];
ans+=(nxt[a[i]+1]-pre[a[i]-1]+1+1)>>1;
}
else if(vs[a[i]-1])
{
ans-=(a[i]-1-pre[a[i]-1]+1+1)>>1;
nxt[pre[a[i]-1]]=a[i];
pre[a[i]]=pre[a[i]-1];
ans+=(a[i]-pre[a[i]]+1+1)>>1;
}
else if(vs[a[i]+1])
{
ans-=(nxt[a[i]+1]-a[i]-1+1+1)>>1;
pre[nxt[a[i]+1]]=a[i];
nxt[a[i]]=nxt[a[i]+1];
ans+=(nxt[a[i]]-a[i]+1+1)>>1;
}
else ans++;
vs[a[i]]=1;
printf("%d ",ans);
}
}
return 0;
}
线段树
菜汪酱刚学了线段树这种数据结构，她写了这样一份代码：
void build(int i, int l, int r) {
L[i] = l; R[i] = r;
if (l == r) return;
int mid = (l+r)/2;
build(i*2, l, mid); build(i*2+1, mid+1, r);
}
对于一棵有 \(n\) 个叶子的线段树，只需要执行 build(1,1,n) 就可以建出线段树。
对于给定的 \(n,x,y\)，她想知道满足 \(x\le L[i]\le R[i]\le y\) 的 \(i\) 的和是多少？
输入格式
第一行一个整数 \(T\) 表示询问组数。
接下来 \(T\) 行每行 \(3\) 个整数 \(n,x,y\) 表示一组询问。
输出格式
对于每组询问，输出一行一个整数表示满足条件的 \(i\) 的和 \(\bmod 10^9+7\)。
之前做过类似的，发现值域很大，但是每次分治后 \(log\) 的状态其实不多，所以可以考虑记搜。
记搜肯定是记录每个长度对应的答案，但是发现答案并不一定。
但是如果长度定了，那么这颗子树的结构就定了，也就是计算方式一定，并且一定满足 \(ans=kx+b\) 的形式。
所以我们可以分别记录上式的常数项和系数，每次带入此时根的值就好了。
设根为 \(x\)，左右的答案分别为 \(k_l(2x)+b_l\)、\(k_r(2x)+b_r\)（注意这里）。写两个函数分别递归寻找系数和常数，注意记搜。
思路还是挺常见的，算是小 trick 吧。
code
#include<bits/stdc++.h>
using namespace std;
const int mod = 1e9+7;
#define LL long long
unordered_map<LL,int> xs,cs;
int T;
LL n,x,y,ans;
inline LL cal(LL len)
{
if(xs.find(len)!=xs.end()) return xs[len];
LL mid=len+1>>1;
return xs[len]=(1+(cal(mid)<<1ll)%mod+(cal(len-mid)<<1ll)%mod)%mod;
}
inline int sol(LL len)
{
if(cs.find(len)!=cs.end()) return cs[len];
LL mid=len+1>>1;
return cs[len]=(sol(mid)+sol(len-mid)+cal(len-mid))%mod;
}
LL dfs(LL i,LL l,LL r)
{
if(x<=l&&y>=r) return (i*cal(r-l+1)%mod+sol(r-l+1))%mod;
LL mid=(r-l>>1)+l,res=0;
if(x<=mid) res=dfs((i<<1ll)%mod,l,mid);
if(y>mid) res=(res+dfs((i<<1ll|1ll)%mod,mid+1,r))%mod;
return res;
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&T);
xs[1]=1; cs[1]=0;
while(T--)
{
scanf("%lld%lld%lld",&n,&x,&y);
printf("%lld\n",dfs(1,1,n));
}
return 0;
}
魔法师
数据结构题没思路可以转化成数学式子的形式思考，更直观。
首先确定答案是 \(max(a_p+a_q,b_p+b_q)\)，也就是如果 \(a_p+a_q \gt b_p+b_q\) 成立，那么会选择 \(a\)，否则选 \(b\)。
化简一下，\(a_p-b_p \gt b_q-a_q\)，这样 \(p\)（假如是法杖）会有一个权值是 \(u=a_p-b_p\)，\(q\)（假如是法咒）会有一个权值是 \(v=b_q-a_q\)，我们可以通过判断这两个权值的大小判断选 \(a\) 还是选 \(b\)。
问题转化为了对于所有 \(u \lt v\) 求 \(b\) 之和最小，对于所有的 \(u \gt v\) 求 \(a\) 之和最小。
为了判断这两个权值的大小，采用分治的方法，也就是线段树，将 \(u,v\) 看成值域上的坐标插入线段树中。
每次合并左右区间时找左区间 \(a_q\) 的最小值和右区间的 \(a_p\) 的最小值，左区间 \(b_p\) 的最小值和右区间的 \(b_q\) 的最小值（还有同一个坐标点上的四个值显然是可以更新的）,计算答案更新，注意还有子区间已经算好的答案也要传上去。
插入删除操作直接用 multiset 维护就好了，注意每个位置要开 \(4\) 个 multiset，每次统计出最小值后再插入进线段树，所以线段树的每个节点只需要维护答案和四个最小值，而不是每个节点开四个 multiset。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 2.5e5+1,INF = 1e9;
int Q,T,ans,c1,c2;
multiset<int> s[N<<1][4];
struct T {int v[4]={INF,INF,INF,INF},sum=INF;} tr[N+1<<3],tmp;
inline void pushup(int k)
{
for(int i=0;i<4;i++) tr[k].v[i]=min(tr[k<<1].v[i],tr[k<<1|1].v[i]);
tr[k].sum=min(tr[k<<1].v[1]+tr[k<<1|1].v[0],tr[k<<1].v[2]+tr[k<<1|1].v[3]);
tr[k].sum=min(tr[k<<1].sum,min(tr[k].sum,tr[k<<1|1].sum));
}
void mdf(int k,int l,int r,int p)
{
if(l==r)
{
tr[k]=tmp;
if(tr[k].v[1]+tr[k].v[0]<=INF||tr[k].v[2]+tr[k].v[3]<=INF)
tr[k].sum=min(tr[k].v[1]+tr[k].v[0],tr[k].v[2]+tr[k].v[3]);
return;
}
int mid=(l+r)>>1;
if(p<=mid) mdf(k<<1,l,mid,p);
else mdf(k<<1|1,mid+1,r,p);
pushup(k);
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d",&Q,&T);
while(Q--)
{
int c,t,a,b,x; scanf("%d%d%d%d",&c,&t,&a,&b);
if(T) a^=ans,b^=ans;
if(c==1)
{
if(t==0)
{
x=a-b+N;
s[x][0].insert(a); s[x][2].insert(b);
for(int i=0;i<4;i++)
{
if(!s[x][i].empty()) tmp.v[i]=*(s[x][i].begin());
else tmp.v[i]=INF;
}
mdf(1,1,N<<1,x);
}
else
{
x=b-a+N;
s[x][1].insert(a); s[x][3].insert(b);
for(int i=0;i<4;i++)
{
if(!s[x][i].empty()) tmp.v[i]=*(s[x][i].begin());
else tmp.v[i]=INF;
}
mdf(1,1,N<<1,x);
}
}
else
{
if(t==0)
{
x=a-b+N;
if(!s[x][2].empty()&&!s[x][0].empty()&&s[x][0].find(a)!=s[x][0].end()&&s[x][2].find(b)!=s[x][2].end())
{
s[x][0].erase(a), s[x][2].erase(b);
for(int i=0;i<4;i++)
{
if(!s[x][i].empty()) tmp.v[i]=*(s[x][i].begin());
else tmp.v[i]=INF;
}
mdf(1,1,N<<1,x);
}
}
else
{
x=b-a+N;
if(!s[x][1].empty()&&!s[x][3].empty()&&s[x][1].find(a)!=s[x][1].end()&&s[x][3].find(b)!=s[x][3].end())
{
s[x][1].erase(a), s[x][3].erase(b);
for(int i=0;i<4;i++)
{
if(!s[x][i].empty()) tmp.v[i]=*(s[x][i].begin());
else tmp.v[i]=INF;
}
mdf(1,1,N<<1,x);
}
}
}
ans=tr[1].sum; if(ans>=N<<1) ans=0;
printf("%d\n",ans);
}
return 0;
}
园艺
看起来不是很难的 dp，容易发现已经经过的点一定是过 \(k\) 的连续段，然后向左右扩展，考虑区间 dp。
$n^2$ 区间 dp
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 2e3+5;
int n,k;
LL s[N],f[N][N][2];
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d",&n,&k);
for(int i=2,x;i<=n;i++) scanf("%d",&x),s[i]=s[i-1]+x;
memset(f,0x3f,sizeof(f));
f[k][k][0]=f[k][k][1]=0;
for(int len=2;len<=n;len++)
{
for(int l=1,r=l+len-1;r<=n;l++,r++)
{
f[l][r][0]=min(f[l+1][r][0]+(s[l+1]-s[l])*(n-r+l),f[l+1][r][1]+(s[r]-s[l])*(n-r+l));
f[l][r][1]=min(f[l][r-1][1]+(s[r]-s[r-1])*(n-r+l),f[l][r-1][0]+(s[r]-s[l])*(n-r+l));
}
}
printf("%lld\n",min(f[1][n][0],f[1][n][1]));
return 0;
}
发现如果还按区间 dp 做不太好优化，因为状态设计的很朴素。
发现每棵草长的速度都是一定的，也就是采到它时它的高度只与当前位置到它的距离有关。
把每棵草初始的权值设为当前位置到它的距离，这样每次向着它走时，由于距离 \(-1\)，高度 \(+1\)，所以不会有变化。
如果背向它走，距离 \(+1\)，高度 \(+1\)，也就是走回去采到它时的高度会 \(+2\)，这样只有背向走的时候会有贡献的变化。
假如有两个点 \(l \le k \le r\)，那么从 \(r\) 走到 \(l\) 会使 \([r+1,n]\) 的每棵草贡献加二倍的 \(dis_{l,r}\)。从 \(l\) 到 \(r\) 同理。
所以我们可以打出以下暴力（其实就是 dij）：
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 2e6+5;
int n,k;
LL f[N],s[N];
priority_queue<pair<LL,int> > q;
bool vs[N];
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d",&n,&k);
for(int i=2,x;i<=n;i++) scanf("%d",&x),s[i]=s[i-1]+x;
memset(f,0x3f,sizeof(f)); f[k]=0;
for(int i=1;i<=n;i++) f[k]+=abs(s[k]-s[i]);
q.push({-f[k],k});
while(!q.empty())
{
int u=q.top().second; q.pop();
if(vs[u]) continue;
vs[u]=1;
if(u<=k)
{
for(int v=k;v<=n;v++) if(!vs[v])
{
if(f[v]>f[u]+2*(u-1ll)*(s[v]-s[u])) f[v]=f[u]+2*(u-1ll)*(s[v]-s[u]),q.push({-f[v],v});
}
}
if(u>=k)
{
for(int v=1;v<=k;v++) if(!vs[v])
{
if(f[v]>f[u]+2*(n*1ll-u)*(s[u]-s[v])) f[v]=f[u]+2*(n*1ll-u)*(s[u]-s[v]),q.push({-f[v],v});
}
}
}
printf("%lld\n",min(f[1],f[n]));
return 0;
}
直接套的 \(dij\) 的板子，还有很多优化余地，比如每次向外更新的一定是当前已经经过的连续段的左右端点，其实不需要 priority_queue。
发现 \(f\) 可以斜率优化（展开发现有乘积项）（复习斜率优化）。
以这个式子为例：
先移项（参变分离），把只含 \(f_l\)（决策点）的项提出来。
看成 \(y=kx+b\) 的形式，\((x,y)=(2l,-f_l+2ls_l-2s_l)\)，注意这里需要考虑斜率 \(s_r\) 的单调性和 \(2l\) 的单调性，分别表示我们要维护的凸包形状和方向。
\(2l\) 是单调递减的，所以我们考虑凸包形状的时候应该也按 \(x\) 递减考虑，斜率 \(s_r\) 递增，也就是维护的凸包长这样：
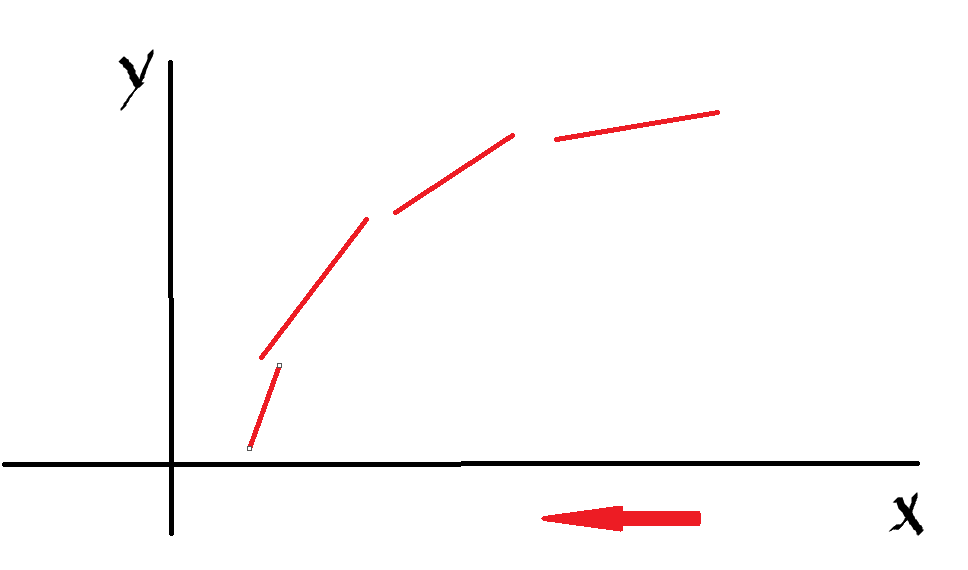
思想就是每次更新 \(l-1\)、\(r+1\) 两项，然后找出当前较小的一端加入队列，也就是会用它更新后面的值，然后扩展这一端的边界。其实就是模拟 \(bfs\) 的操作。
遇到最大坑点就是考虑横坐标和斜率的单调性，其他都还好做，注意 __int128，计算斜率时如果把除法乘过去会炸 long long。
题解
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 2e6+5;
int n,k;
LL f[N],s[N];
int q1[N],q2[N],l1=1,l2=1,r1=1,r2=1;
inline LL cal1(int x) {return -1*(f[x]-2*x*s[x]+2*s[x]);}
inline LL cal2(int x) {return -1*(f[x]+2*n*s[x]-2*s[x]*x);}
inline void mdf1(int l)
{
while(l1<r1&&((__int128)cal1(q1[r1-1])-cal1(q1[r1]))*(q1[r1]-l)>=(__int128)(cal1(q1[r1])-cal1(l))*(q1[r1-1]-q1[r1])) r1--;
q1[++r1]=l;
}
inline void mdf2(int r)
{
while(l2<r2&&((__int128)cal2(q2[r2])-cal2(q2[r2-1]))*(r-q2[r2])<=(__int128)(cal2(r)-cal2(q2[r2]))*(q2[r2]-q2[r2-1])) r2--;
q2[++r2]=r;
}
inline void ans2(int l)
{
int v=l;
while(l2<r2&&cal2(q2[l2+1])-cal2(q2[l2])>=(__int128)2*(q2[l2+1]-q2[l2])*s[v]) l2++;
int u=q2[l2];
f[v]=f[u]+2*(n*1ll-u)*(s[u]-s[v]);
}
inline void ans1(int r)
{
int v=r;
while(l1<r1&&cal1(q1[l1])-cal1(q1[l1+1])<=(__int128)2*(q1[l1]-q1[l1+1])*s[v]) l1++;
int u=q1[l1];
f[v]=f[u]+2*(u-1ll)*(s[v]-s[u]);
}
int main()
{
// freopen("cut1.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d",&n,&k);
for(int i=2,x;i<=n;i++) scanf("%d",&x),s[i]=s[i-1]+x;
memset(f,0x3f,sizeof(f)); f[k]=0;
for(int i=1;i<=n;i++) f[k]+=abs(s[k]-s[i]);
int l=k-1,r=k+1; mdf1(k); mdf2(k);
while(l>=1&&r<=n)
{
ans1(r); ans2(l);
if(f[l]<=f[r]) mdf1(l--);
else mdf2(r++);
}
printf("%lld\n",min(f[1],f[n]));
return 0;
}
后记
Day 1 电脑在最后半个小时被膝盖薄纱了，极限打暴力。（下午又干了一次，糖）
Day 2 考试提前 5min，后面两题暴力都没交上。。。
感觉自己题解写得很shi。
