2024.8.18 模拟赛 22
模拟赛
T1 先崩,然后电脑又崩。
题面都在这里了
T1 2-Coloring
原题3100,张口放T1(这是原话)
看起来像 dp,推了两个小时大力分讨,最后式子比我命还长。刚推出来就发现假了
正解差不多人类智慧吧,也可能只是小 trick。
对于整张图,考虑最终染色的“形状”。(下面这个样子)
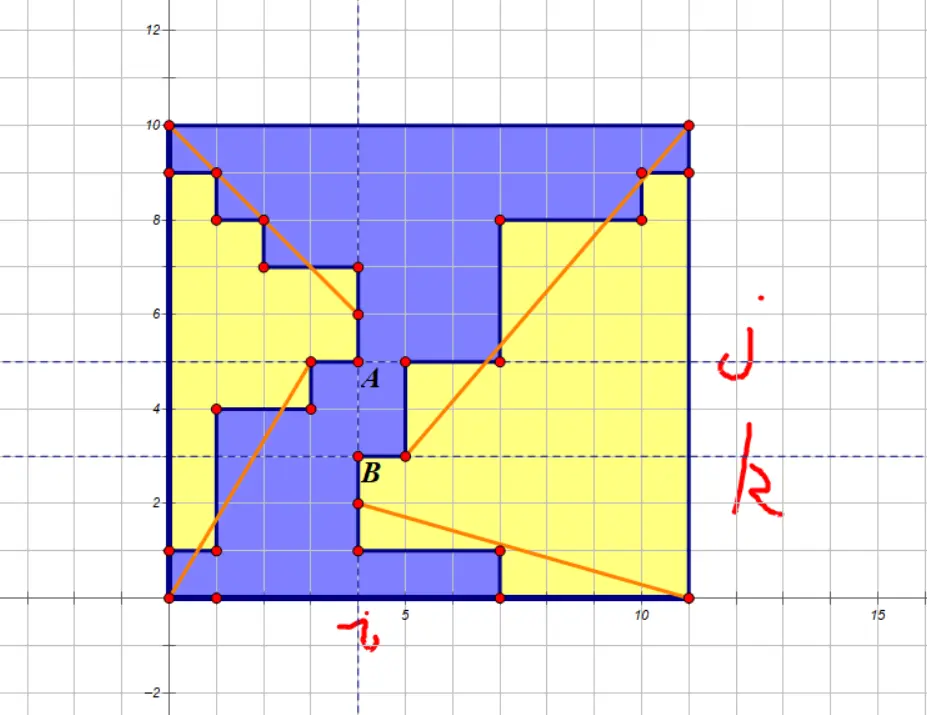
图片来自 题解 CF1503E 2-Coloring,讲得真的很好。
同一颜色最多会产生两个连通块,如果中间恰好交于一点一共就有四个连通块。
如果我们想对这个图的“形状”进行计数,那么就要找到能够代表图的特征点以便不重不漏,并且应该可以计数。
对于这道题来说,有一个关键就是每一列不能全放、每一行不能不放,在“形状”上表示中间有且只有一列可以将两侧黄色连通块分开。
所以我们可以枚举这个临界,然后计算当临界列为 \(i\) 时的方案。
这就将黄色连通块分开了。黄色块会与第 \(i\) 列有两段相交的区间 \((l_1,r_1)\)、\((l_2,r_2)\),我们将 \(r1,l2\) 这对点作为我们计数的标准。
样整个图就变成了四个部分,每个部分都很规整的将两种颜色分成两半。

画图条件有限。
因此我们分别算每个块的方案数就好了!最后把四个块的乘起来。
那么怎么单独求方案数呢?有一种很巧妙的方法就是转化为路径问题。由于要满足选的 \(A,B\) 点是 \(r_1,l_2\) 的位置,所以实际计算时就是算顶点到上面标出的四个点的路径方案数。
这时我们只考虑了黄色被分割的情况,而蓝色被分割其实就是 \(n,m\) 交换一下。
这样先枚举 \(i\),再枚举 \(A,B\) 的复杂度显然是 \(n^3\) 的,如何优化?
假如 \(A\) 点在上方,那么 \(B\) 点其实就是在 \([1,A]\) 的所有情况的和,可以前缀和维护,注意 \(A=B\) 的时候特殊处理。
然后终于做完了。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 4999,mod = 998244353;
int n,m;
LL f[N],inv[N],ans;
void init(int NM)
{
f[0]=inv[0]=inv[1]=1;
for(int i=2;i<=NM;i++) inv[i]=(mod-mod/i)*inv[mod%i]%mod;
for(int i=1;i<=NM;i++) f[i]=f[i-1]*i%mod,inv[i]=inv[i-1]*inv[i]%mod;
}
LL way(int x,int y) {return f[x+y]*inv[x]%mod*inv[y]%mod;}
int main()
{
freopen("magic.in","r",stdin);
freopen("magic.out","w",stdout);
scanf("%d%d",&n,&m);
init(n+m);
for(int i=1;i<=m-1;i++)
{
LL sum=0;
for(int j=1;j<=n-1;j++)
{
sum=(sum+way(i,j-1)*way(i-1,n-j))%mod;
ans=(ans+sum*way(m-i-1,j)%mod*way(m-i,n-j-1))%mod;
}
}
swap(n,m);
for(int i=1;i<=m-1;i++)
{
LL sum=0;
for(int j=1;j<=n-1;j++)
{
ans=(ans+sum*way(m-i-1,j)%mod*way(m-i,n-j-1))%mod;
sum=(sum+way(i,j-1)*way(i-1,n-j))%mod;
}
}
printf("%lld\n",(ans<<1ll)%mod);
}
T2 连通块
需要用到树的直径的小性质:
-
距离树内一点 \(u\) 最远的点一定为树的直径的端点。
-
两棵树合并后树的直径就是两棵树之前的直径端点间的最大距离(四个点里选两个)。
也就是树的直径可以合并。
对于原题中的删边操作,我们可以转化为逆向的加边操作。这样用并查集维护连通块,并且树的直径可以直接合并。就很简单了。
(第一次有关树据结构的题能自己打出来还一遍过了)
code
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+5;
int n,m,d[N][2],ans[N];
int head[N],tot;
struct E {int u,v;} e[N<<1],ed[N];
inline void add(int u,int v) {e[++tot]={head[u],v}; head[u]=tot;}
struct Q {int tp,x;} q[N<<1];
bool vs[N];
namespace LCA
{
int dfn[N],cnt,st[N][21],dep[N],lg[N];
void dfs(int u,int f)
{
dfn[u]=++cnt; st[cnt][0]=f; dep[u]=dep[f]+1;
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v; if(v==f) continue;
dfs(v,u);
}
}
inline int get(int x,int y) {return dfn[x]<dfn[y]?x:y;}
void init()
{
for(int i=2;i<=n;i++) lg[i]=lg[i>>1]+1;
for(int i=1;i<=20;i++)
for(int j=1;j+(1<<i)-1<=n;j++)
st[j][i]=get(st[j][i-1],st[j+(1<<i-1)][i-1]);
}
int lca(int x,int y)
{
if(x==y) return x;
if((x=dfn[x])>(y=dfn[y])) swap(x,y);
int k=__lg(y-x); x++;
return get(st[x][k],st[y-(1<<k)+1][k]);
}
inline int dis(int x,int y) {return dep[x]+dep[y]-(dep[lca(x,y)]<<1);}
}; using namespace LCA;
namespace DSU
{
int fa[N];
void init() {for(int i=1;i<=n;i++) fa[i]=i,d[i][0]=d[i][1]=i;}
int find(int x) {return x==fa[x]?x:fa[x]=find(fa[x]);}
void merge(int x,int y)
{
int fx=find(x),fy=find(y);
int t1=d[fx][0],t2=d[fx][1],tmp=dis(t1,t2),t3;
for(int i=0;i<=1;i++) for(int j=0;j<=1;j++)
{
t3=dis(d[fx][i],d[fy][j]);
if(t3>tmp) t1=d[fx][i],t2=d[fy][j],tmp=t3;
}
t3=dis(d[fy][1],d[fy][0]); if(t3>tmp) t1=d[fy][0],t2=d[fy][1],tmp=t3;
fa[fy]=fx; d[fx][0]=t1; d[fx][1]=t2;
}
int get(int x)
{
int fx=find(x);
return max(dis(x,d[fx][0]),dis(x,d[fx][1]));
}
};
int main()
{
freopen("block.in","r",stdin);
freopen("block.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<n;i++)
{
int x,y; scanf("%d%d",&x,&y);
add(x,y); add(y,x); ed[i]={x,y};
}
dfs(1,0); init(); DSU::init();
for(int i=1;i<=m;i++)
{
int c,x; scanf("%d%d",&c,&x);
q[i]={c,x}; if(c==1) vs[x]=1;
}
for(int i=1;i<n;i++) if(!vs[i]) DSU::merge(ed[i].u,ed[i].v);
int cnt=0;
for(int i=m;i>=1;i--)
{
if(q[i].tp==1) DSU::merge(ed[q[i].x].u,ed[q[i].x].v);
else ans[++cnt]=DSU::get(q[i].x);
}
for(int i=cnt;i>=1;i--) printf("%d\n",ans[i]);
return 0;
}
T3 军队
这其实才是数据结构。。。
题面挺抽象的,但题意奇怪但简单。
我们可以用扫描线处理矩形加,因为只需要维护每一行的信息,所以其实还挺简单的。
重点在于维护什么信息?
我们想要知道每一行中 \(\ge k\) 的个数,并且 \(k \le 30\),首先想到维护 \(\lt k\) 的个数,并从 \(k\) 上操作。
其实小于 \(k\) 的数值只会有 \(k\) 个,我们可以维护前 \(k\) 小的值和数量,\(\lt k\) 的个数一定已经被包含在里面了。
线段树合并时类似归并,挺暴力的。查询只会查整行,所以暴力遍历前 \(k\) 小的值就行了。
每一行记录两种“性别”中较小的那个(因为要配对)。最后回答时贪心,\(lower_bound\) 找一下多少行能取 \(\lfloor \frac{y}{2} \rfloor\)。剩下的顶着取就行了。
这里其实就是 \(\sum a \times (y-a)\),维护一下 \(a\) 和 \(a^2\) 的前缀和(后缀和也可以呢)。(\(a\) 就是那个)。
(一开始用 vector,写法简洁又亲民,\(\mathbb{T}\) 飞了,被迫换数组。)
code
#include<bits/stdc++.h>
#define scan __builtin_scanf
#define print __builtin_printf
using namespace std;
#define fi first
#define se second
#define P pair<int,int>
#define LL long long
const int N = 3e5+5;
int n,m,c,K,Q,s[N];
LL ans,s1[N],s2[N];
struct M {int l,r,v;}; vector<M> v[N];
namespace SEG
{
struct T {int l,r,lz,cnt=0,kthf[11],kths[11];} tr[N<<2];
inline void pushup(int k)
{
tr[k].cnt=0;
int sz1=tr[k<<1].cnt,sz2=tr[k<<1|1].cnt;
int l=1,r=1;
while(l<=sz1&&r<=sz2&&tr[k].cnt<K)
{
if(tr[k<<1].kthf[l]<tr[k<<1|1].kthf[r]) tr[k].kthf[++tr[k].cnt]=tr[k<<1].kthf[l],tr[k].kths[tr[k].cnt]=tr[k<<1].kths[l++];
else if(tr[k<<1].kthf[l]>tr[k<<1|1].kthf[r]) tr[k].kthf[++tr[k].cnt]=tr[k<<1|1].kthf[r],tr[k].kths[tr[k].cnt]=tr[k<<1|1].kths[r++];
else tr[k].kthf[++tr[k].cnt]=tr[k<<1].kthf[l],tr[k].kths[tr[k].cnt]=tr[k<<1].kths[l]+tr[k<<1|1].kths[r],l++,r++;
}
while(l<=sz1&&tr[k].cnt<K) tr[k].kthf[++tr[k].cnt]=tr[k<<1].kthf[l],tr[k].kths[tr[k].cnt]=tr[k<<1].kths[l++];
while(r<=sz2&&tr[k].cnt<K) tr[k].kthf[++tr[k].cnt]=tr[k<<1|1].kthf[r],tr[k].kths[tr[k].cnt]=tr[k<<1|1].kths[r++];
}
inline void pushdown(int k)
{
if(tr[k].lz)
{
int lz=tr[k].lz; tr[k].lz=0;
for(int i=1;i<=tr[k<<1].cnt;i++) tr[k<<1].kthf[i]+=lz;
for(int i=1;i<=tr[k<<1|1].cnt;i++) tr[k<<1|1].kthf[i]+=lz;
tr[k<<1].lz+=lz; tr[k<<1|1].lz+=lz;
}
}
inline void bui(int k,int l,int r)
{
tr[k].l=l; tr[k].r=r;
if(l==r) return (tr[k].kthf[++tr[k].cnt]=0,tr[k].kths[tr[k].cnt]=1),void(0);
int mid=l+r>>1;
bui(k<<1,l,mid); bui(k<<1|1,mid+1,r);
pushup(k);
}
inline void mdf(int k,int l,int r,int v)
{
if(tr[k].l>=l&&tr[k].r<=r)
{
for(int i=1;i<=tr[k].cnt;i++) tr[k].kthf[i]+=v;
tr[k].lz+=v; return;
}
pushdown(k);
int mid=tr[k].l+tr[k].r>>1;
if(l<=mid) mdf(k<<1,l,r,v);
if(r>mid) mdf(k<<1|1,l,r,v);
pushup(k);
}
}; using namespace SEG;
int main()
{
freopen("ar.in","r",stdin);
freopen("army.out","w",stdout);
scan("%d%d%d%d%d",&n,&m,&c,&K,&Q);
for(int i=1;i<=c;i++)
{
int x1,x2,y1,y2; scan("%d%d%d%d",&x1,&y1,&x2,&y2);
v[x1].push_back({y1,y2,1}); v[x2+1].push_back({y1,y2,-1});
}
bui(1,1,m);
for(int i=1;i<=n;i++)
{
int res=0;
for(M j:v[i]) mdf(1,j.l,j.r,j.v);
for(int i=1;i<=tr[1].cnt;i++)
{
if(tr[1].kthf[i]>=K) break;
res+=tr[1].kths[i];
}
s[i]=min(res,m-res);
}
sort(s+1,s+1+n);
for(int i=n;i>=1;i--) s1[i]=s1[i+1]-s[i]*s[i],s2[i]=s2[i+1]+s[i];
for(int i=1;i<=Q;i++)
{
int x,y; scan("%d%d",&x,&y);
int p=lower_bound(s+1,s+1+n,y/2)-s;
if(n-p+1>=x) print("%lld\n",1ll*x*(y/2)*(y-(y/2)));
else print("%lld\n",1ll*(n-p+1)*(y/2)*(y-(y/2))+s1[n-x+1]-s1[p]+1ll*y*(s2[n-x+1]-s2[p]));
}
return 0;
}
T4 棋盘
咕咕咕。。。

