2024.7.23 模拟赛6
模拟赛
T1 就是 \(\mathbb{A}\) 不了！！！
T1 mod M
唐了一个半小时，最后 40min 才看出来，莫名挂 \(6\) 分。
如果只考虑 \(mod 2\) 的情况。最终答案最多有两种。
那显然，我们只需要考虑什么时候能剩下一种。
只有在 \(n\) 个数都同余时才能剩下一种。
既然都同余，就是任意两数的差的 \(gcd\) 都不为 \(1\)。
思维不够严密，有 \(n=2\) 或其他卡边界的状态会寄，以下方法可以避免。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5+5;
int n,a[N];
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
sort(a+1,a+1+n);
for(int i=2;i<=n;i++)
{
if(a[i]==a[i+1]) continue;
if(__gcd(a[i]-a[1],a[i]-a[i-1])==1) return printf("2\n"),0;
}
printf("1\n");
return 0;
}
T2 Number of Multisets
其实挺简单的一道 dp，赛时唐。
想到去年 5K 口胡的题：
- \(k\) 个正整数相加等于 \(m\)，求方案数。
正解类似分讨，\(f_{i,j}\) 表示选 \(i\) 个数和为 \(j\) 的方案数：
-
考虑包含 \(1\) 的方案，将 \(1\) 删掉，那么这类方案的数量为 \(f_{i-1,j-1}\)。
-
考虑剩下的方案一定都不包含 \(1\)，那么把 \(i\) 个数都减去 \(1\)。方案数为 \(f_{i,j-i}\)。
回来看这道题，我们仍是把所有方案划分成两类：包含 \(1\)，不包含 \(1\)。
那么所有包含 \(1\) 的方案可以由 \(f_{i-1,j-1}\) 得到，不包含 \(1\) 的可以把每个数乘二，由 \(f_{i,j\ times 2}\) 得到。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 3e3+5,mod = 998244353;
int n,k;
int f[N][N];
int main()
{
scanf("%d%d",&n,&k);
f[0][0]=1;
for(int i=1;i<=n;i++)
{
f[i][i]=1;
for(int j=i;j>=1;j--)
{
f[i][j]=(f[i-1][j-1]+f[i][j<<1])%mod;
}
}
printf("%d\n",f[n][k]);
return 0;
}
T3 Simultaneous Sugoroku
首先拿暴力和值域的部分分，都好拿。值域的其实有一点启发正解。
移动机器人其实和移动原点是等价的，假如我们把每次操作看成对原点移动，那么会有一个显然的性质：
- 关于原点对称的两个点在之后的操作中位置一定是对称的。
举例：假如原点移动到了 \(x\)，那么 \(x-i\) 和 \(x+i\) 最终答案一定为相反数。
因此每次都有一半的数轴可以直接对称过去，也就是每次能删掉一部分。
我们可以用带权并查集维护对称次数，并查集的范围就是值域范围。
维护一个区间表示数轴上的实际范围，另一个维护以当前原点为中心左右延申的距离，每次合并较小的一半（启发式？）。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 3e5+5,M = 1e6+6;
int n,m,a[N],b[N],ans[M];
int l,r,mid,L,R;
int fa[M];bool tag[M];
int find(int x)
{
if(fa[x]!=x)
{
int fx=fa[x];
fa[x]=find(fa[x]);
tag[x]^=tag[fx];
}
return fa[x];
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<=m;i++) scanf("%d",&b[i]);
l=a[1]; r=a[n]; L=l; R=r;
for(int i=l;i<=r;i++) fa[i]=i;
for(int i=1;i<=m;i++)
{
if(l>0) l-=b[i],r-=b[i];
else l+=b[i],r+=b[i];
if(l<=0&&r>=0)
{
int x=R-r,fx=find(x);
ans[fx]=i;
if(-l<r)
{
for(int i=1;i<=-l;i++) fa[x-i]=x+i,tag[x-i]^=1;
L=x+1; l=1;
}
else
{
for(int i=1;i<=r;i++) fa[x+i]=x-i,tag[x+i]^=1;
R=x-1; r=-1;
}
}
}
for(int i=1;i<=n;i++)
{
int x=find(a[i]);
if(ans[x]) printf("Yes %d\n",ans[x]);
else printf("No %d\n",(r-R+x)*(tag[a[i]]?-1:1));
}
return 0;
}
T4 Triangles
这么多天第一次改到 T4!!!
还是 dp，每个顶点记录它向左上，右上，左 延伸的最大距离，首先考虑左和左上的限制如果想延伸一定在这个范围内。
然后对于满足这个限制的点看它向右上延伸距离是否满足。（说不太清，看图更不清）
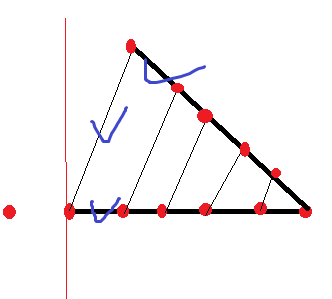
只有三个方向都满足才能转移。定义 \(v1\) 为向右上延伸距离，\(v2\) 为左上延伸最大距离。\(pre\) 为左侧延伸最远的点。
我们考虑每一个点的贡献，也就是每个点会有一个管辖范围。我们分别记它对后面的贡献，和前面哪些值会对它造成贡献。
我们开树状数组，查询 \(x \in [pre,i-1]\) 并且 \(x+v2_x \ge i\)。也就是每一个 \(x+v2_x \ge i\) 都会有贡献。
（下图：黑色是 \(k\) 能为哪些点有贡献，黄色是区间加，蓝色是区间减，红色是统计答案所在区间）
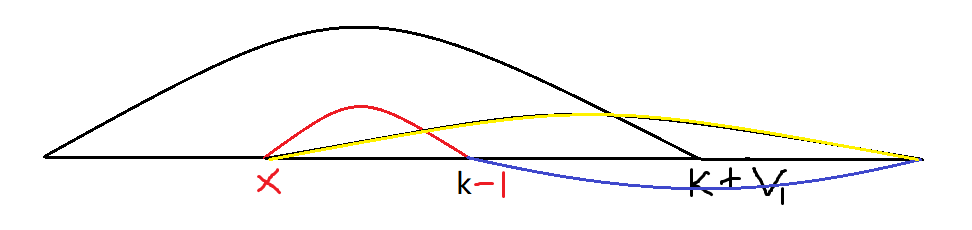
记得反转求一次反向的三角形。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 12005;
#define LL long long
int n,m;
string s[N];
int v1[N>>1][N],v2[N>>1][N],b[N];
LL ans;
struct BIT
{
int n,c[N];
void mdf(int x,int v)
{
for(;x;x-=(x&-x)) b[x]+=v;
}
int que(int x)
{
int res=0;
for(;x<=n;x+=(x&-x)) res+=b[x];//注意树状数组维护的是前缀和，而不是普通的后缀。
return res;
}
void clear()
{
for(int i=1;i<=n;i++) b[i]=0;
}
} c;
void reverse()
{
for(int i=1;i<=(n>>1);i++) swap(s[i],s[n-i+1]);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
s[i][j]==0x5c?s[i][j]=0x2f:(s[i][j]==0x2f?s[i][j]=0x5c:0);
}
vector<int> p[N>>2];
vector<pair<int,int> >q[N>>2];
void work(int st)
{
for(int i=1;i<=n;i+=2)
{
c.clear();
for(int j=(i+st)%4,k=1,pre=1;j<=m;j+=4,k++)
{
v2[i][j]=s[i-1][j-1]==0x5c?v2[i-2][j-2]+1:0;
v1[i][j]=s[i-1][j+1]==0x2f?v1[i-2][j+2]+1:0;
s[i][j-1]!=0x2d?pre=k:pre;
p[k].clear(); q[k].clear();
p[k].push_back(k+v1[i][j]);
if(max(pre,k-v2[i][j])-1>0) q[max(pre,k-v2[i][j])-1].push_back(make_pair(k,-1));
if(k-1>0) q[k-1].push_back(make_pair(k,1));
}
for(int j=(i+st)%4,k=1;j<=m;j+=4,k++)
{
for(int h:p[k]) c.mdf(h,1);
for(pair<int,int> h:q[k]) ans+=h.second*c.que(h.first);
}
}
}
int main()
{
scanf("%d%d",&n,&m); c.n=n+m; n=(n<<1)-1; m=(m<<1)-1;
for(int i=0;i<=n;i++) getline(cin,s[i]),s[i]=' '+s[i];
work(0);
reverse();
work(s[1][1]==0x78?0:2);
printf("%lld\n",ans);
return 0;
}
