2024.7.20模拟赛3
模拟赛
昨天的题解还在咕。。。今天的又来了。。。
T1 Simple Math 2
签到题，推一推式子就好了。
\[\lfloor {\frac{a^b}{c}} \rfloor\mod c= x
\]
\[\lfloor {\frac{a^b}{c}} \rfloor = k \times c + x
\]
\[\frac{a^b-(a^b \mod c)}{c} = k \times c + x
\]
\[a^b-(a^b \mod c)= k \times c^2 + x \times c
\]
\[(a^b-(a^b \mod c)) \mod c^2=x \times c
\]
\[\frac{(a^b-(a^b \mod c)) \mod c^2}{c}=x
\]
\(c\) \(1e4\) 直接搞。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
LL b,c,C;
LL qpow(LL x,LL y)
{
LL res=1;
while(y)
{
if(y&1) res=(res*x)%C;
x=(x*x)%C; y>>=1;
}
return res;
}
int main()
{
scanf("%lld%lld",&b,&c);
C=c*c;
LL d=qpow(10,b),e=d%c;
printf("%lld\n",(d-e)/c);
return 0;
}
T2 Mister B and PR Shifts
线性做法。我们考虑每一位数的贡献，然后大力分讨。
-
如果一开始 \(a[i] \le i\)，那么随着这个数向右移，贡献越来越大。
-
如果一开始 \(a[i] \gt i\)，贡献会先变小再变大，会有一个转折点。
我们可以开一个桶记录到转折点距离为 \(d\) 的数的个数为 \(cnt[d]\)。
当我们移动 \(d\)时，就会有 \(cnt[d]\) 个数变为第一种。 -
最后一个数会变成第一个，特判一下。
代码不太好打，这次呵题解对压行有了更深理解，最近好多题都是直接考虑每个数的贡献。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+6;
#define LL long long
int n,a[N],cnt[N<<1],cnt1,cnt2,k;
LL ans,s1,s2;
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]),a[i]>i?(s1+=a[i]-i,cnt[a[i]-i]++,cnt1++):(s2+=i-a[i],cnt2++);
ans=s1+s2;
for(int i=1;i<=n;i++) s1-=cnt1,s2+=cnt2,cnt1-=cnt[i],cnt2+=cnt[i],cnt2--,s2-=((n+1)-a[n-i+1]),
a[n-i+1]>1?++cnt[a[n-i+1]-1+i],s1+=a[n-i+1]-1,cnt1++:++cnt2,s1+s2<ans&&(ans=s1+s2,k=i);
printf("%lld %d\n",ans,k);
return 0;
}
T3 Yazid 的新生舞会
先转化题意，对于一个数 \(w\)，\(S_i\) 表示前 \(i\) 个数中 \(w\) 的出现次数。
则对于一段区间 \([l+1,r]\)，\(S_r-S_l \gt \frac{r-l}{2}\)，所以 \(2S_r-r \gt 2S_l-l\)。
也就是我们要求的就是 \(2S_i-i\) 的逆序对。
但如果暴力求复杂度仍然不是很优。我们发现总数只有 \(n\) 个数，也就是两个 \(w\) 之间会有很大无用的间距。
大概是这样子：
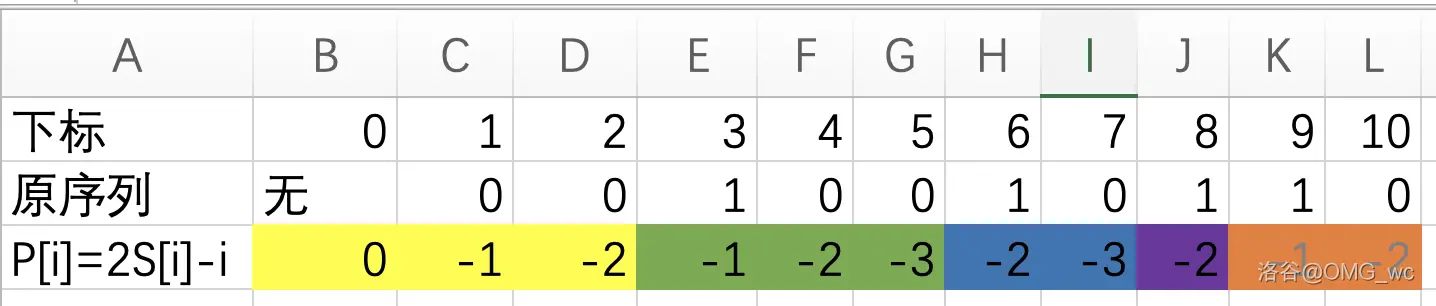
图片来自 OMG_wc
中间其实就是一段段的等差数列，公差为 \(1\)。也就是这是在值域上连续递减的一段。
所以我们用树状数组求逆序对时可以直接进行区间加操作。直接维护区间信息。
对于权值为 \(T_i\) 的数，它的贡献是 \(\sum_{j=1}^{i-1}c_j\)，而对于 \([x,y]\) 中的数，它们的贡献是 \(\sum_{i=x}^{y}T_i\)。
所以问题就变成了二阶前缀和，区间修改。
既然树状数组实现区间修改，我们考虑维护差分数组，然后求三阶前缀和。三阶前缀和可以用三个树状数组维护：
\[k \le j \le i
\]
\[\begin{aligned}
ans_x&=\sum\limits_{i=1}^{x}\sum\limits_{j=1}^{i}\sum\limits_{k=1}^{j}d_k\\
&=\sum\limits_{k=1}^{x}\sum\limits_{j=k}^{x}\sum\limits_{i=j}^{x}d_k\\
&=\sum\limits_{k=1}^{x}\sum\limits_{j=1}^{x-k+1}\sum\limits_{i=1}^{x-j+1}d_k\\
&=\sum\limits_{k=1}^{x}\frac{(x+2-k)(x+1-k)}{2}d_k\\
&=\frac{(x+2)(x+1)}{2}\sum\limits_{k=1}^{x}d_k-\frac{2x+3}{2}\sum\limits_{k=1}^{x}d_k\cdot k+\frac{1}{2}\sum\limits_{k=1}^{x}d_k\cdot k^2
\end{aligned}
\]
所以维护 \(d_k \times k\)、\(d_k \times k^2\)、\(d_k \times k^3\)。
上述只是对于某一个数值的统计，每次要还原树状数组。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 5e5+5;
int n,a[N],type;
LL ans,c1[N<<1],c2[N<<1],c3[N<<1];
vector<int> b[N];
inline void add(int x,LL v,int m)
{
for(int i=x;i<=m;i+=(i&-i))
c1[i]+=v, c2[i]+=v*x, c3[i]+=v*x*x;//加的都是 x
}
inline LL ask(int x)
{
LL res=0;
for(int i=x;i;i-=(i&-i)) res+=c1[i]*(x+2)*(x+1)-c2[i]*(x*2+3)+c3[i];
return res>>1;
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d",&n,&type);
for(int i=1;i<=n;i++) scanf("%d",&a[i]),b[a[i]].push_back(i);
int pyl=n+1;//偏移量
for(int i=0;i<n;i++)
{
b[i].push_back(n+1);
for(int j=0,lst=0;j<b[i].size();j++)
{
int y=2*j-lst+pyl,x=2*j-(b[i][j]-1)+pyl;//2S-i
ans+=ask(y-1)-(x>=3?ask(x-2):0);
add(x,1,2*n+1); add(y+1,-1,2*n+1);
lst=b[i][j];
}
for(int j=0,lst=0;j<b[i].size();j++)//还原
{
int y=2*j-lst+pyl,x=2*j-(b[i][j]-1)+pyl;
add(x,-1,2*n+1); add(y+1,1,2*n+1);
lst=b[i][j];
}
}
printf("%lld\n",ans);
return 0;
}
T4 上帝造题的七分钟 2 / 花神游历各国
有一个很显然的性质，\(a=10^11\) 进行开方操作最多 \(6\) 次就会变成 \(1\)。
最多修改操作只有 \(6n\) 次，可以考虑爆修。
于是爆修线段树：
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 1e5+5;
int n,q;
LL a[N];
struct T
{
int l,r;
LL sum;
} tr[N<<2];
inline void pushup(int k)
{
tr[k].sum=tr[k<<1].sum+tr[k<<1|1].sum;
}
inline void bui(int k,int l,int r)
{
tr[k].l=l; tr[k].r=r;
if(l==r) return tr[k].sum=a[l],void(0);
int mid=l+r>>1;
bui(k<<1,l,mid); bui(k<<1|1,mid+1,r);
pushup(k);
}
inline void mdf(int k,int l,int r)
{
if(tr[k].sum==tr[k].r-tr[k].l+1) return;//注意剪枝
if(tr[k].l==tr[k].r) return tr[k].sum=sqrt(tr[k].sum),void(0);
int mid=tr[k].l+tr[k].r>>1;
if(l<=mid) mdf(k<<1,l,r);
if(r>mid) mdf(k<<1|1,l,r);
pushup(k);
}
inline LL que(int k,int l,int r)
{
if(l<=tr[k].l&&r>=tr[k].r)
return tr[k].sum;
int mid=tr[k].l+tr[k].r>>1; LL res=0;
if(l<=mid) res+=que(k<<1,l,r);
if(r>mid) res+=que(k<<1|1,l,r);
return res;
}
int main()
{
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);//卡常
cin>>n;
for(int i=1;i<=n;++i) cin>>a[i];
bui(1,1,n);
cin>>q;
while(q--)
{
int x,y,z; cin>>x>>y>>z;
if(y>z) swap(y,z);
if(x==0) mdf(1,y,z);
else cout<<que(1,y,z)<<'\n';
}
return 0;
}
优点是不用动脑子（如果想不到就没脑子了），缺点是大力卡常。
正解其实就是用树状数组维护，减小常数，至于已经变成 \(1\) 的数可以用并查集维护。
并查集的 trick？
码量友好：
code
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+5;
#define LL long long
int n,q,fa[N]; LL a[N],c[N];
int find(int x)
{
if(fa[x]!=x) fa[x]=find(fa[x]);
return fa[x];
}
void add(int x,LL v)
{
for(;x<=n;x+=(x&-x)) c[x]+=v;
}
LL que(int x)
{
LL res=0;
for(;x;x-=(x&-x)) res+=c[x];
return res;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%lld",&a[i]),add(i,a[i]),fa[i]=i; fa[n+1]=n+1;
scanf("%d",&q);
while(q--)
{
int c,l,r; scanf("%d%d%d",&c,&l,&r);
if(l>r) swap(l,r);
if(c==1) printf("%lld\n",que(r)-que(l-1));
else
{
for(int i=l;i<=r;)
{
int fi=find(i);
if(fi!=i) i=fi;
else
{
LL t=sqrt(a[i]);
add(i,t-a[i]); a[i]=t;
if(a[i]==1) fa[i]=i+1,i=find(i);
else i++;
}
}
}
}
return 0;
}
