LCA 补充
LCA
之前学废了，回来补。
倍增版
首先是最常见的倍增版子，思路好理解，按倍增记录 \(father\)，然后同时往上跳。
注意最后跳到的是那个 \(x \ne y\) 的，也就是 \(lca\) 的儿子，所以最后要返回父亲。
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5+5;
int n,m,rt;
int head[N],tot;
struct E{int u,v;} e[N<<1];
void add(int u,int v) {e[++tot]={head[u],v}; head[u]=tot;}
int dep[N],fa[30][N];
void dfs(int u,int f)
{
dep[u]=dep[f]+1; fa[0][u]=f;
for(int i=1;i<=25;i++)
fa[i][u]=fa[i-1][fa[i-1][u]];
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v; if(v==f) continue;
dfs(v,u);
}
}
int lca(int x,int y)
{
if(dep[x]<dep[y]) swap(x,y);
for(int i=25;i>=0;i--) if(dep[fa[i][x]]>=dep[y]) x=fa[i][x];
if(x==y) return x;
for(int i=25;i>=0;i--) if(fa[i][x]!=fa[i][y]) x=fa[i][x],y=fa[i][y];
return fa[0][x];
}
int main()
{
scanf("%d%d%d",&n,&m,&rt);
for(int i=2;i<=n;i++)
{
int x,y; scanf("%d%d",&x,&y);
add(x,y); add(y,x);
}
dep[rt]=1;//!!!
dfs(rt,0);
while(m--)
{
int x,y; scanf("%d%d",&x,&y);
printf("%d\n",lca(x,y));
}
return 0;
}
DFS 序版
我们记录每个点的 \(dfn\) 时间戳和 dfs 序。
应用的性质是 \(lca\) 的 dfs 序不会出现在 \(u\) 和 \(v\) 之间出现。并且是在它们之前出现。
其中 dfs 序体现在 dfs 遍历时维护的 \(st\)，也就是记录父亲。
最终 \(st[i][u]\) 表示的是以 \(u\) 的时间戳为起点，在dfs序上向后延长 \(2^i\) 位的深度最小值的节点的父亲，也就是 \(dfn\) 最小节点。
这里很神奇的是查询能直接查到 \(lca\)，因为我们查询的是 \([dfn_u,dfn_v]\) 这段 \(dfs\) 序上的父亲时间戳最小值显然这个点一定就是 \(lca\)。
（挂张图）
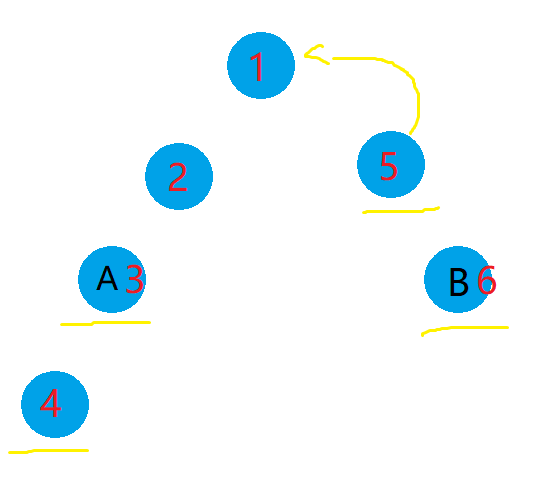
#include<bits/stdc++.h>
using namespace std;
#define mi(x,y) (dfn[x]<dfn[y]?(x):(y))
const int N = 5e5+5;
int n,m,rt;
int head[N],tot;
struct E {int u,v;} e[N<<1];
inline void add(int u,int v) {e[++tot]={head[u],v}; head[u]=tot;}
int dfn[N],cnt,st[N][25];
void dfs(int u,int f)
{
dfn[u]=++cnt; st[cnt][0]=f;
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v; if(v==f) continue;
dfs(v,u);
}
}
int lca(int x,int y)
{
if(x==y) return x;
if((x=dfn[x])>(y=dfn[y])) swap(x,y); x++;
int k=__lg(y-x+1);
return mi(st[x][k],st[y-(1<<k)+1][k]);
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d%d",&n,&m,&rt);
for(int i=1;i<n;i++)
{
int x,y; scanf("%d%d",&x,&y);
add(x,y); add(y,x);
}
dfs(rt,0);
for(int i=1;i<=20;i++)
for(int j=1;j+(1<<i)-1<=n;j++)
st[j][i]=mi(st[j][i-1],st[j+(1<<(i-1))][i-1]);
while(m--)
{
int x,y; scanf("%d%d",&x,&y);
printf("%d\n",lca(x,y));
}
return 0;
}
树链剖分版
划分轻重链后往上跳，直到跳到同一条链上，其实就是借助了树剖的 dfs，亲民。
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5+5;
int n,m,rt;
int head[N],tot;
struct E{int u,v;} e[N<<1];
void add(int u,int v) {e[++tot]={head[u],v}; head[u]=tot;}
int sz[N],dep[N],fa[N],son[N],top[N];
void dfs1(int u,int f)
{
fa[u]=f; dep[u]=dep[f]+1; sz[u]=1; son[u]=-1;
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v;
if(v==f) continue;
dfs1(v,u);
sz[u]+=sz[v];
if(son[u]==-1||sz[son[u]]<sz[v]) son[u]=v;
}
}
void dfs2(int u,int t)
{
top[u]=t;
if(son[u]==-1) return ;
dfs2(son[u],t);
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v;
if(v!=fa[u]&&v!=son[u]) dfs2(v,v);
}
}
int lca(int x,int y)
{
while(top[x]!=top[y])
{
if(dep[top[x]]>=dep[top[y]]) x=fa[top[x]];
else y=fa[top[y]];
}
return dep[x]<dep[y]?x:y;
}
int main()
{
scanf("%d%d%d",&n,&m,&rt);
for(int i=2;i<=n;i++)
{
int x,y; scanf("%d%d",&x,&y);
add(x,y); add(y,x);
}
dfs1(rt,0); dfs2(rt,rt);
while(m--)
{
int x,y; scanf("%d%d",&x,&y);
printf("%d\n",lca(x,y));
}
return 0;
}
写在最后
虽然原博列举了很多 dfs 序 LCA 的优点，但是缺点也有一点点吧。
倍增方法可以处理 k 级祖先，这在一些树上跳的题目中很重要。
树剖可以顺便求出 lca，用途也比较广。
dfs 序码量较短，复杂度更优。
