奇妙的Fibonacci(Dirichlet 前缀和)
奇妙的Fibonacci
题目描述
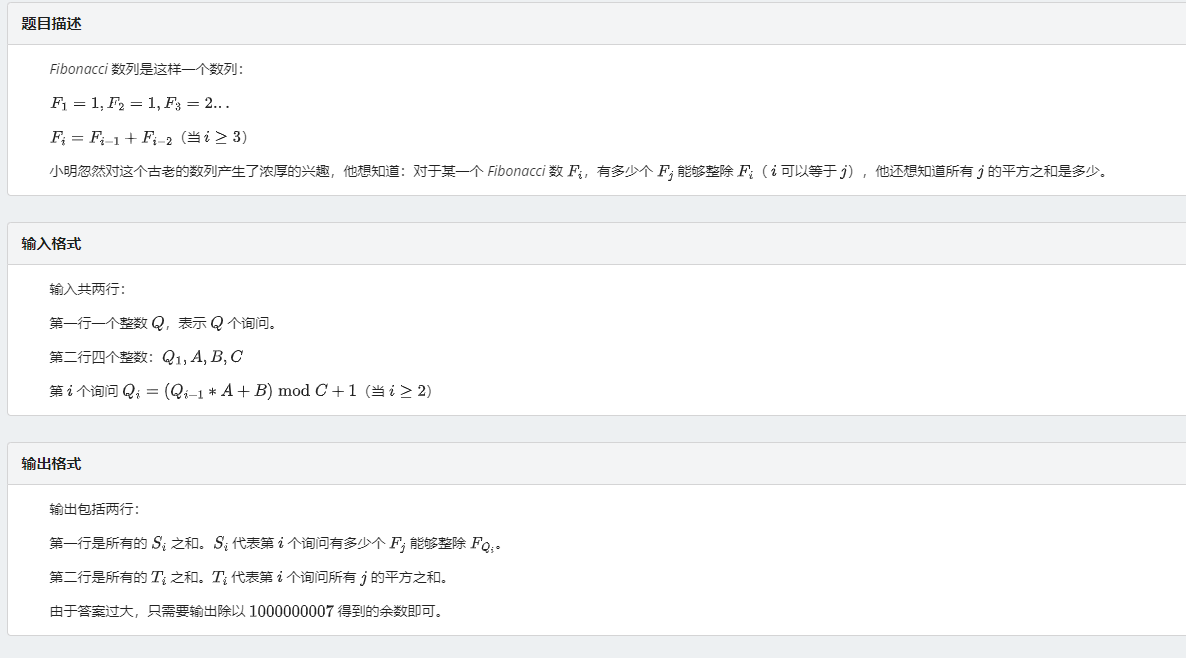
(听 5K 讲才知道原来是水题)
(听 qinyun 讲完发现又不是)
本文尽量解释 Fibonacci、高位前缀和 以及 Dirichlet 前缀和等,能力有限,不喜勿喷
Fibonacci
Fibonacci 数列具有一个众所周知的性质 $$ gcd(F_i,F_j)=F_{gcd(i,j)}$$
证明如下
\(\begin{aligned} F_i &=F_{i-1}+F_{i-2}\\ &=F_{i-1} \times F_{2}+F_{i-2} \times F_{1}\\ &=(F_{i-2}+F_{i-3}) \times F_{2}+F_{i-2} \times F_{1}\\ &=F_{i-2} \times (F_{1}+F_{2})+F_{i-3} \times F_{2}\\ &=F_{i-2} \times F_{3}+F_{i-3} \times F_{2}\\ &\dots\dots\\ \therefore F_{n+m} &=F_{n} \times F_{m+1} + F_{n-1} \times F_{m}\\\\ \end{aligned}\)
\(\begin{aligned} \because gcd(F_{i},F{i-1}) &=gcd(F_{i}-F_{i-1},F_{i-1})\\ &=gcd(F_{i-2},F_{i-1})\\ &\dots\dots\\ &=gcd(F_{2},F_{3})\\ &= 1\\\\ \end{aligned}\)
\(\begin{aligned} \therefore gcd(F_{n+m},F_{n}) &= gcd(F_{n} \times F_{m+1} + F_{n-1} \times F_{m},F{n})\\ &= gcd(F_{n-1} \times F_{m},F{n})\\ &= gcd(F_{n},F_{m})\\\\ \end{aligned}\)
\(\because \begin{cases} gcd(n+m,n) = gcd(n,m) \\ gcd(F_{n+m},F_{n}) = gcd(F_{n+m},F_{n}) \end{cases}\)
\(\therefore gcd(F_{n+m},F_{n})=F_{gcd(n+m,n)}\)
$\therefore F{j} \mid F{j} \Rightarrow j \mid i $
于是,我们会发现 奇妙的 Fibonacci 与 Fibonacci 一点关系都没有。其实就是求 $$i=\sum_{j \mid i}j^2$$
Dirichlet 前缀和
转化为前缀和
5K 讲的???东西,目前的理解就是求一个数的所有约数的和(或者有关约数的函数的和)。式子如下: $$b_j=\sum_{i|b_j}a_i$$
这里的 \(a_i\) 可以是一些奇奇妙妙的东西。
根据唯一分解定理:$$b=\prod_i p_i^{c_i}$$
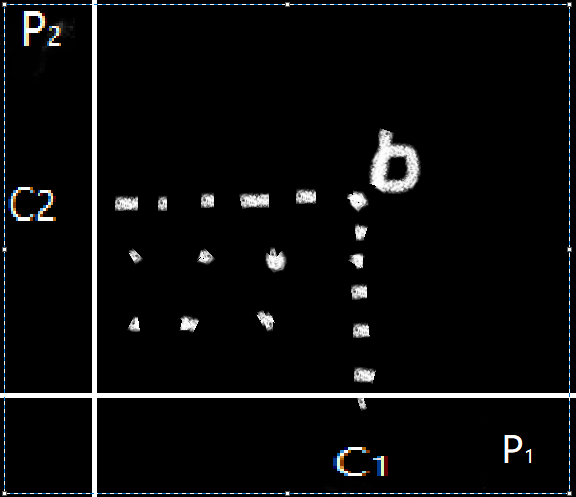
如果我们把 \(b\) 的每一个质因子 \(p_i\) 看成高维空间中的一维,\(c_i\) 看成这一维方向上向量的长度,
\(b\) 表示的就是空间中的一个向量(或点),而 \(b\) 的所有约数就是 \(b\) 与坐标轴围成的封闭图形中的点(以二维为例)。
那么我们求的就是 \(b\) 这个点的前缀和。
重新回忆一下前缀和,在求二维前缀和时,我们进行的操作是先横向做一遍 $$F_{i,j}=F_{i-1,j}+F{i,j}$$
然后再纵向做一遍 $$F_{i,j}=F_{i,j-1}+F_{i,j}$$
以此类推,我们求高维前缀和就是分别对每一维进行一遍上述操作。
具体如何在这道题中实现呢?
实现
以这个代码为例:
for(int i=1;i<=cnt;i++)
for(int j=1;j*prime[i]<=n;j++)
a[prime[i]*j]+=a[j];
a[j] 表示的就是 \(j\) 的所有约数对应的 \(a[j]\) 的和,我们把 \(j\) 分解后得到:$$j=\prod_i p_i^{c_i}$$
所以 \(j\) 也就是高维空间中的一个点(等同于上文的 \(b\)), prime[i]*j 的操作就相当于把 \(j\) 的坐标从 \((c_i ,\cdots)\) 转移到了 \((c_i +1,\cdots)\),
每一个点 \(j\) 都会更新在 \(p_i\) 维上坐标 \(+1\) 的点,在 \(p_i\) 方向上递推更新前缀和,
然后每一个质因子 \(prime\) 被遍历的过程就是遍历维度的过程,对每一维都进行类似操作后对整个空间前缀和的维护就完成了。
完整代码如下:
#include<bits/stdc++.h>
using namespace std;
const int N = 1e7+5,mod = 1e9+7;
typedef long long LL;
LL n,q,a,b,c,ans1,ans2,s[N],t[N];
bool v[N];
int main()
{
freopen("fibo.in","r",stdin);
freopen("fibo.out","w",stdout);
scanf("%lld%lld%lld%lld%lld",&n,&q,&a,&b,&c); v[1]=1;
for(LL i=1;i<=1e7;i++) t[i]=i*i%mod,s[i]=1;
for(int i=2;i<=1e7;i++) if(!v[i])
for(int j=i,k=1;j<=1e7;j+=i,k++)
v[j]=1, s[j]=(s[j]+s[k])%mod, t[j]=(t[j]+t[k])%mod;
for(int i=1;i<=n;i++)
{
ans1=(ans1+s[q]+(q&1))%mod;
ans2=(ans2+t[q]+(q&1)*4)%mod;
q=(q*a+b)%c+1;
}
printf("%lld\n%lld\n",ans1,ans2);
return 0;
}
复杂度 \(O(nloglogn)\),有更快的线性筛做法,但这种不用动脑子


