二分图
二分图
定义:一张图的 \(N\) 个节点可以分为 \(A,B\) 两个非空集合,满足同一个集合中的任意两个点没有连边。
集合 \(A,B\) 分别叫做二分图的左部和右部,如图所示:
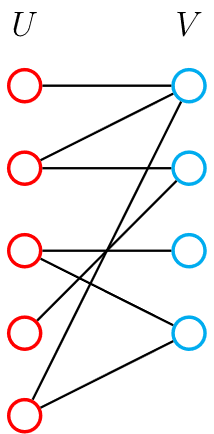
二分图的判定
交替染色,只有相邻的点颜色不一样时才可能是二分图,
定理:二分图一定不存在奇环(易证)。
判定:搜索 \(dfs\) 或 \(bfs\) 都行。
bool dfs(int u, int fa, int color)
{
col[u] = color; //给当前结点染色
for (int i = head[u]; i; i = e[i].nxt)
{
int v= e[i].tv;
if (v== fa) continue;
if (col[v] == color)
return 0; // 子结点有颜色且与当前结点染色相同
if (col[v] == 0 && !dfs(v, u, 3-color))
return false; // 尝试染色失败
}
return true;
}
bool work()
{
for (int i = 1; i <= n; i++)
{
if (col[i] == 0)
{
col[i] = 1; // 用1和2染色
if (!dfs(i, 0, 1))
return 0;
}
}
return 1;
}
二分图的最大匹配
二分图的匹配:找出一个边集 \(M\),使任意两条边没有公共端点。属于 \(M\) 的边叫 匹配边,其端点叫 匹配点。
交错路:从一个 非匹配点出发,依次经过匹配边,非匹配边……的一条路径。
增广路:从一个 非匹配点 出发,走 交错路,到达另一个 非匹配点 的路径。
增广路的性质:
-
增广路上的边数为奇数。
-
路径上第 \(1、3、5……\) 条边为非匹配边,第 \(2、4、6……\) 条边为匹配边,所以非匹配边数量比匹配边数量多一。
-
我们从一个非匹配点出发走增广路,这条路径上的匹配边构成一个 匹配 ,这时对所有边进行取反(匹配变非匹配,非匹配变匹配),得到新的匹配比原来那个长度多一。
匈牙利(叙利亚,lyx,intr)算法
求最大匹配可以看做是一个舞蹈队的人分成了两个集合,给点集1中的点从点集2中找舞伴,点集1中的点都是男的,点集2中的点都是女的,每个人都有若干个意向的舞伴。
男找女,如果女没有舞伴,直接匹配。如果女有舞伴,那么考虑这名舞伴能不能妥协换一个,把当前的女伴让出来。
也就是根据增广路的性质看看能不能走出一条更长的增广路,然后取反状态。
bool mp[N][N],vs[N*N];
bool dfs(int u)
{
for(int i=0;i<n;i++) if(!vs[i]&&mp[u][i])
{
vs[i]=1;
if(!mt[i]||dfs(mt[i]))//这里dfs的是match
{
mt[i]=u;
return 1;
}
}
return 0;
}
int intr()
{
int res=0;
memset(mt,0,sizeof(mt));
for(int i=0;i<n;i++)
{
memset(vs,0,sizeof(vs));
if(dfs(i)) res++;
}
return res;
}
最小顶点覆盖
顶点覆盖:设点集 \(V^{'}\),图中每一条边至少有一个顶点在集合 \(V^{'}\)。
最小顶点覆盖:顾名思义,使 \(V^{'}\) 中的元素尽量少。
结论一:最小顶点覆盖=最大二分图匹配
(感性理解:二分图任意两条边之间都没有公共点,所以点的覆盖作用被最大化了)
最大独立集
独立集:点集 \(V^{'}\) 中任意两个点之间没有连边。(例如二分图的左部和右部)。
结论二:最大独立集=总点数-最小顶点覆盖=总点数-最大二分图匹配
(感性理解:最小顶点覆盖保证每一条边至少有一个点被选,把这些点去掉相当于去掉所有边,剩下的点就没有边了)
总结
关于建图
二分图看起来只是把图分成了两部分,但其实这两部分可以抽象的作为 冲突 的两端。
如果两者之间有冲突则建边,没有冲突则属于二分图的同一部,长、常用来求 不包含冲突的最大集合,也就是最大独立集。
关于双向边
最大二分图匹配的流程是由左部找有部的点,其实是有向图。
一般我们希望二分图的左右部分别代表不同的意义,构成有向图,如男女,行列……
但更多时候题目没有明确给出左部和右部,虽然这个图仍具有二分图的性质,我们也不知无向边两端哪个是左部,
我们在连双向边时会将所有点各在左右部放一次,也就是建两条边,让这个双倍的点集自发的跑出二分图的形状(前提它是二分图)
这时就会出现重复的边,也就是我们跑出的最大二分图匹配其实是双向边的,也就是二倍。
所以最后答案要除二。
关于行与列
在有关地图放置的题目中我们常将行与列作为 冲突 ,跑二分图最大匹配。
但如果地图中有一些 障碍物 呢?这时冲突依然可以成立,只是 行 与 列 的定义不同了。
我们以题为例:
放置机器人
这道题冲突是明显的,两个机器人不能处于同一行或同一列(先不考虑障碍),
这时我们对行与列的定义是这样的
性质1. 同一行(或列)中只能放一个。
性质2. 不同行(或列)之间不会有影响。
现在,让我们加入障碍物。障碍物会把一行(或列)分成若干个部分,
每个部分依旧满足 性质1 ,每一个 部分,只能放一个。
性质2 呢?也满足!
于是 “行” 和 “列” 的定义扩大了,我们可以通过记录 “分块” 的方式重组行列。
照常跑 \(intr\) 就行了。


