OKR-Periods of Words

[POI2006] OKR-Periods of Words

题面翻译

对于一个仅含小写字母的字符串 $a$，$p$ 为 $a$ 的前缀且 $p\ne a$，那么我们称 $p$ 为 $a$ 的 proper 前缀。

规定字符串 $Q$ 表示 $a$ 的周期，当且仅当 $Q$ 是 $a$ 的 proper 前缀且 $a$ 是 $Q+Q$ 的前缀。若这样的字符串不存在，则 $a$ 的周期为空串。

例如 ab 是 abab 的一个周期，因为 ab 是 abab 的 proper 前缀，且 abab 是 ab+ab 的前缀。

求给定字符串所有前缀的最大周期长度之和。

样例 #1

样例输入 #1

8
babababa

样例输出 #1

24

数据范围

$k(1\le k\le 1000\text{0}00)$

解析

字符串周期，阅读理解题。

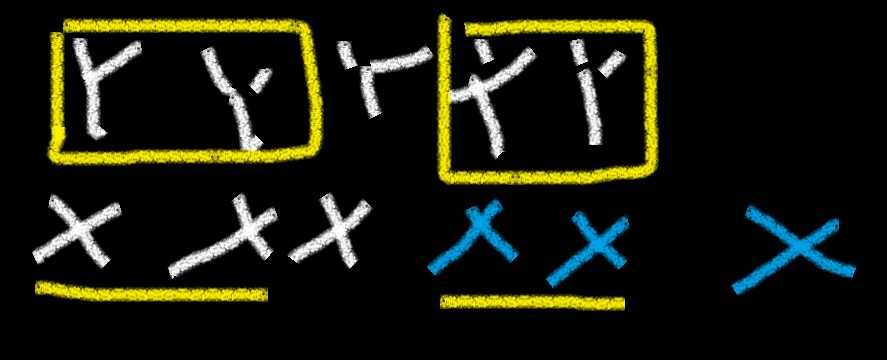
如上图，将白 $X$ 复制一倍，这时 $Y$ 是所有 $X$ 的子串，所以黄色框起来的 $Y$ 必须相同。

为了让 $X\times 2$ 刚好和 $Y$ 对齐，$Y$ 前后相同的部分应尽量短，也就是求最短的 $border$.

答案长度就是 $len-p_{min}$ (减去后面那两个 $Y$)，

求最短的前缀函数见 动物园，

但是暴力求解会 $\mathbb{T}$ ，可采用记忆化，每次找到最小的就把当前 $p$ 置成最小值。

code

#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+5;
long long n,p[N];
string s;
long long ans;
int main()
{
	scanf("%lld",&n); cin>>s;
	for(int i=1;i<n;i++)
	{
		int j=p[i-1];
		while(j&&s[i]!=s[j]) j=p[j-1];
		p[i]=j+(s[i]==s[j]);
	}
	for(int i=1;i<n;i++)
	{
		int j=p[i]; if(!j) continue;
		while(p[j-1]) j=p[j-1];
		p[i]=j;
		ans+=i+1-j;	
	}
	printf("%lld\n",ans);
	return 0;
}

注意

KMP j=p[j-1] ，中的 j-1 是为了让长度和下标对齐。

P.S

有人疑惑为什么不用判断 $|2Q|<|a|$ 的情况。

我们可以假设 $|2Q|<|a|$ ，则 $a$ 最短的 $border$ 长度一定大于 $\lfloor \frac{|a|}{2}\rfloor$ ，也就是会有重叠的，

由于这部分重叠的既是前缀字符串的后缀，又是后缀字符串的前缀，所以整个字符串一定还有一个更短的 $border$ ，

因此这个有重复部分的 $border$ 不是最短的，冲突，假设不成立。

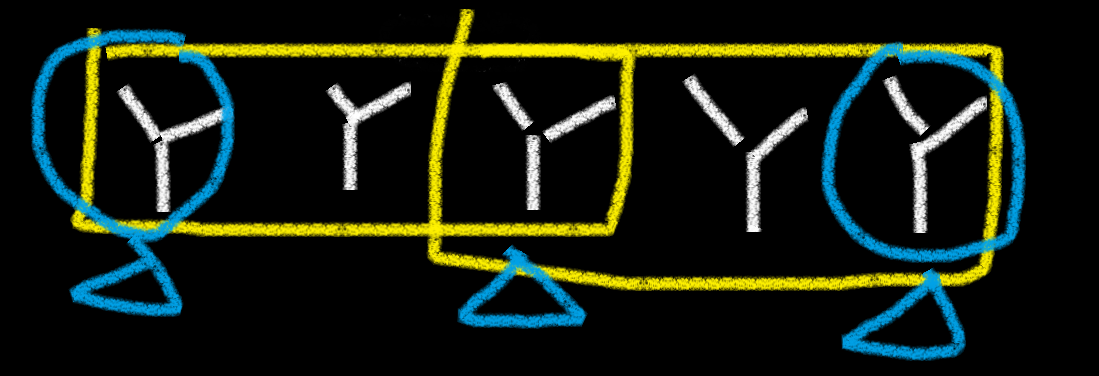
蓝三角的 $Y$ 都是相同的，所以圈起来的更短。