U423621 [HDK - NRC] Sqen Paradox
[HDK - NRC] Sqen Paradox
题目描述
给定一个长度为 \(n\) 的数列 \(S\).
询问在给定区间 \([l,r]\) 内最长的没有重复元素的区间长度.
输入格式
第一行两个整数 \(n,m\).
第二行 \(n\) 个整数,描述数列 \(S\).
随后 \(m\) 行,每行一个询问.
输出格式
\(m\) 行,请你对每个询问操作输出一行答案.
样例 #1
样例输入 #1
5 3
1 2 3 3 4
1 3
2 4
1 5
样例输出 #1
3
2
3
提示
样例解释
-
询问
1 3,连续的最长区间为 \([1,3]\). -
询问
2 4,区间为 \([2,3]\). -
询问
1 5,区间为 \([1,3]\).
数据约定
输入数据满足 \(n,m\le 10^{5},S_{i}\le 10^{9}\).
解析一(唐氏 \(O(n^2)\))(非正解)
(以下做法来自 \(GGrun\))
题干很简单,乍一看线段树呀,分块呀等数据结构。
但其实这道题要简单的多。
既然 找"没有重复元素的"区间,那么我们可以维护一个类似前缀的东西。
也就是找出每个点能向左延长多少。
所以只需要找出最后一个出现重复的数据就好了。
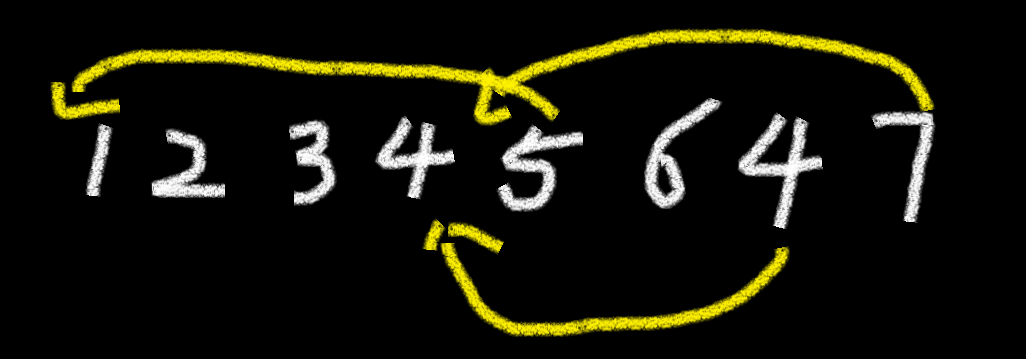
如图,\(1...6\) 前面都没有和自己重复的,直到又碰到一个 \(4\) ,
\(7\) 前面虽然没有和自己重复的,但是前面有一对 \(4\) ,所以只能到 \(4\) 。
综上:记录一个 \(k\) ,表示 最大长度只能为 \(k+1...i\) ,和每一个数上一次出现的位置。
取最大值更新 \(k\) ,就好啦!
(狂 \(\mathbb{D}\) 水数据)
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+9;
int n,m,s[N],tot;
int cnt[N],qian[N];
map<int,int> mp;
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d",&s[i]);
if(mp.find(s[i])==mp.end()) mp[s[i]]=++tot,s[i]=tot;
else s[i]=mp[s[i]];
}
int k=0;
for(int i=1;i<=n;i++)
{
k=max(k,cnt[s[i]]); cnt[s[i]]=i;
qian[i]=k;
}
while(m--)
{
int ans=1;
int x,y;
scanf("%d%d",&x,&y);
for(int i=x;i<=y;i++)
{
ans=max(ans,i-max(x-1,qian[i]));
}
printf("%d\n",ans);
}
return 0;
}
解析二(\(O(nlogn)\))
上述唐氏做法经过 \(O(n^2)\) 的查询后成功 \(\mathbb{T}\) 了。
预处理没问题,查询可以分为两部分,一部分从 \(l\) 往右找断点 \(mid\),
另一部分找到断点后取 \((mid,r]\) 为右端点向左最大长度。
在预处理时找到左端点后我们顺便记录当前的右端点,也就是向右移的最大长度。

左端点向右扩展简单,\((mid,r]\) 找到的最大长度一定不会碰到左端点(易证:否则就在前一段)。
因为我们从左端点已经找出了一个长度 \(mid-x\) ,如果想要一个更大的并且起点不在左端点,那么它的右端点一定在 \((mid,r]\)。
最大值用st表维护,复杂度 \(O(nlogn)\) .
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+9;
int n,m,s[N],tot;
int cnt[N],st[N][40],R[N];
unordered_map<int,int> mp;
int que(int l,int r)
{
if(l>r) return 0;//注意
int k=log2(r-l+1);
return max(st[l][k],st[r-(1<<k)+1][k]);
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d",&s[i]);
if(mp.find(s[i])==mp.end()) mp[s[i]]=++tot;
s[i]=mp[s[i]];
}
int l=0;
for(int i=1;i<=n;i++)
{
l=max(l,cnt[s[i]]); cnt[s[i]]=i;
R[l]=max(R[l],i);//R记右端点
st[i][0]=i-l;//区间为(l,i]
}
for(int i=1;i<n;i++)
if(!R[i]) R[i]=R[i-1];//把中间那些被跳过去的点也更新一下
for(int j=1;j<=30;j++)
for(int i=1;i+(1<<j)-1<=n;i++)
st[i][j]=max(st[i][j-1],st[i+(1<<j-1)][j-1]);
while(m--)
{
int x,y;
scanf("%d%d",&x,&y); x--;//因为前面计的(l,r],所以这里最远到x-1
int mid=min(y,R[x]);
printf("%d\n",max(mid-x,que(mid+1,y)));
}
return 0;
}
2024.5.11 HDK 加强数据。
2024.8.8 找到原题/相似题???数列找不同


