字符串基础：Hash，KMP，Trie树

Hash

把一个字符串映射成一个整数，可以方便的比较两个字符串是否相等，

计算 \(Hash\) 值:

\[\displaystyle \sum_{i=0}^{len-1}(s[i] \times B^{len-1-i})(mod\;M) \]

这里的 \(B\) 是任取的一个大小合适的数，\(M\) 就是为了把算出来的值映射到 \([0,M-1]\) 的范围内，

既然是 \(mod\) ，就会有重复的值，也就是 “Hash碰撞”（“Hash冲突”），两个不相同的字符串映射到了同一个值上。

“Hash碰撞”不可避免，只要知道模数 \(M\) 就一定可以卡，一般 \(M\) 我们取一个较大的质数，

不常用的最好（防止常用的被卡），更方便的可以用 \(unsigned \;long \;long\) 的自然溢出，

最保险的是取双模数，即每个串 Hash 两个值，分别比较。

[板子]

code

#include<bits/stdc++.h>
using namespace std;
const int N = 1000005;
const int M = 99995699,B = 233;
typedef unsigned long long ULL;
int t,n,m;
string a,b;
ULL hs[1000005],p[1000005];
ULL gh(int l,int r)
{
	return (hs[r]-hs[l-1]*p[r-l+1]);
}
int main()
{
	scanf("%d",&t);
	while(t--)
	{
		long long ans=0;
		cin>>a>>b;
		n=a.length(), m=b.length();
		p[0]=1;
		ULL tmp=0;
		for(int i=0;i<n;i++) tmp=tmp*B+a[i];
		for(int i=0;i<m;i++)
		{
			hs[i+1]=hs[i]*B+b[i];
			p[i+1]=p[i]*B;
		}
		for(int i=1,j=n;j<=m;j++,i++)
			if(gh(i,j)==tmp) ans++;
		printf("%d\n",ans);
	}
	return 0;
}

碱基序列[dp]

碱基序列

\(dp[i][j]\) 表示在前 \(i\) 个碱基串中选总长度为 \(j\) 串的 \(ans\)，

思路类似背包吧，\(dp[i][j]\) 可以由 \(dp[i-1][j-len_{(i,k)}]\) 转移过来。

code

#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ULL;
const int B = 233,mod = 1e9 + 7;
int k;
ULL hs[10005],p[10005];
int dp[105][10005];
string t;
ULL get_hash(string x)
{
	ULL res=0,len=x.length();
	for(int i=0;i<len;i++) res=res*B+x[i];
	return res;
}
ULL get(int l,int r)
{
	return hs[r]-hs[l-1]*p[r-l+1];
}
int main()
{
	scanf("%d",&k);
	cin>>t; int n=t.length();
	p[0]=1; dp[0][n]=1;
	for(int i=0;i<n;i++)
	{
		hs[i+1]=hs[i]*B+t[i];
		p[i+1]=p[i]*B;
		dp[0][i]=1;
	}
	for(int i=1;i<=k;i++)
	{
		int x; string s;
		scanf("%d",&x);
		for(int j=1;j<=x;j++)
		{
			cin>>s; int len=s.length();
			ULL tmp=get_hash(s);
			for(int l=1,r=len;r<=n;l++,r++)
			{
				if(get(l,r)==tmp)
				dp[i][r]=(dp[i-1][l-1]+dp[i][r])%mod;
			}
		}
	}
	long long ans=0;
	for(int i=1;i<=n;i++) ans=(ans+dp[k][i])%mod;
	printf("%lld\n",ans);
	return 0;
}

注意

字符串从 \(0\) 开始，

hs数组下标从 \(1\) 开始！！！（唐）

KMP

1.一些定义

2.前缀函数

KMP前置芝士，给出字符串 \(S\), \(\pi[i]\) 是子串 \(S[0...i]\) 最长的 \(border\) （见上文）。

1.暴力

可以暴力方法直接求，依次比较子串。

int pi[N];
void get()
{
	int n=s.length();
	for(int i=1;i<n;i++)
	{
		for(int j=i;j>=0;j--)
		{
			if(s.substr((0,j))==s.substr(i-j+1,j))
			{
				pi[i]=j; break;
			}
		}
	}
}

2.优化一

每一个前缀函数值最多比前一个增加 \(1\) ，因此我们可以修改 \(j\) 遍历的起点，从 \(\pi[i-1]+1\) 开始就好啦。

(变化不大)

int pi[N];
void get()
{
	int n=s.length();
	for(int i=1;i<n;i++)
	{
		for(int j=pi[i-1]+1;j>=0;j--)
		{
			if(s.substr((0,j))==s.substr(i-j+1,j))
			{
				pi[i]=j; break;
			}
		}
	}
}

3.优化二（成品）

以下图为例

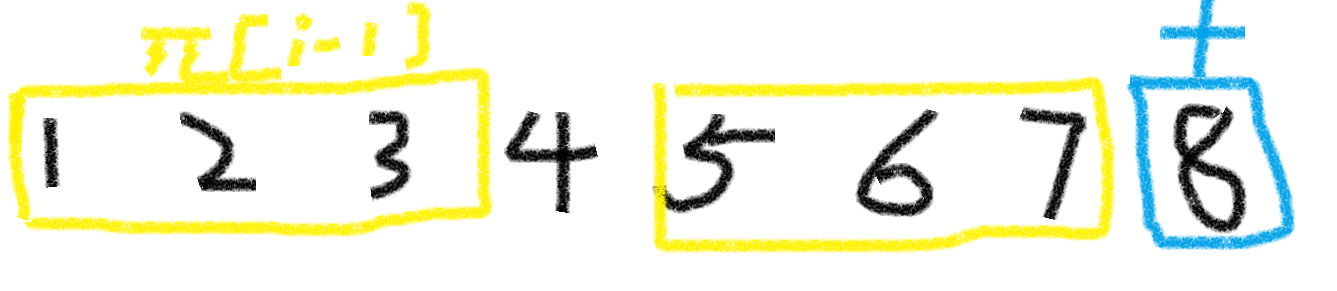
已经求出 \(\pi[i-1]\) ，正在加入第 \(8\) 个。

因为最大为 \(\pi[i-1]+1\) ，所以我们首先判断 \(s[i]\) 与 \(s[\pi[i]]\) (注意下标与长度不一样),

如果一样，那么直接就是 \(\pi[i-1]+1\),

如果不一样，我们需要缩短长度，如下图。

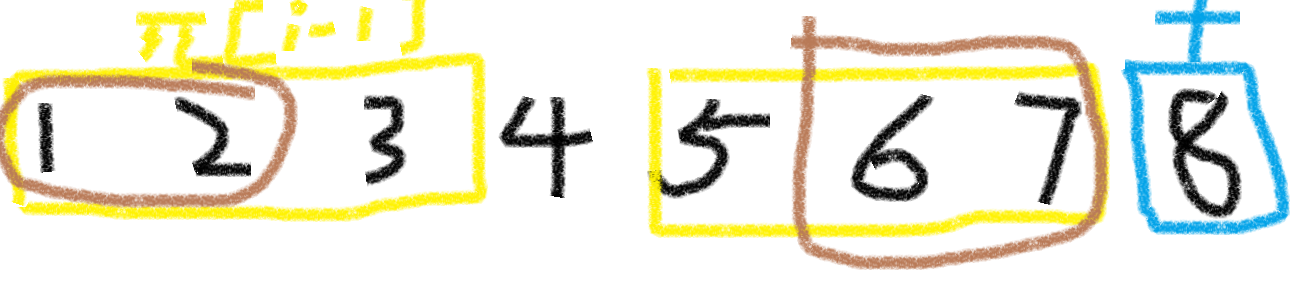
首先要满足 \(1,2\) 和 \(6,7\) 部分是相同的，而由于 \(1,2,3\) 和 \(5，6，7\) 已经构成前缀函数，是相同的，

所以 \(6,7\) 和 \(2,3\) ，也是相同的，因此我们只需要找到 \(S[0...\pi[j-1]]\) 的前缀数组，在进行相同的判断就好啦！

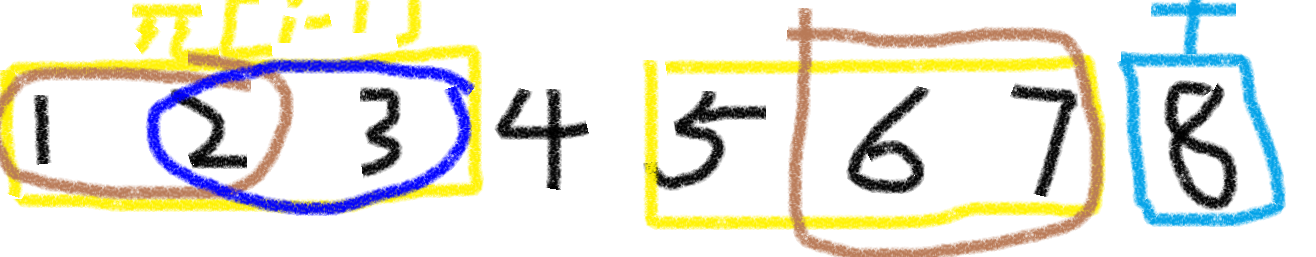
int pi[N];
void get()
{
	int n=s.length();
	for(int i=1,j=0;i<n;i++)
	{
		while(j&&s[i]!=s[j]) j=pi[j-1];
		pi[i]=j+=(s[i]==s[j]);
	}
}

KMP

匹配字符串，我们可以把文本串和匹配串拼接起来（匹配串在前，中间用分隔符隔开），

对这个拼接后的字符串求前缀函数，那么如果长度等于匹配串，那么就说明找到一个。

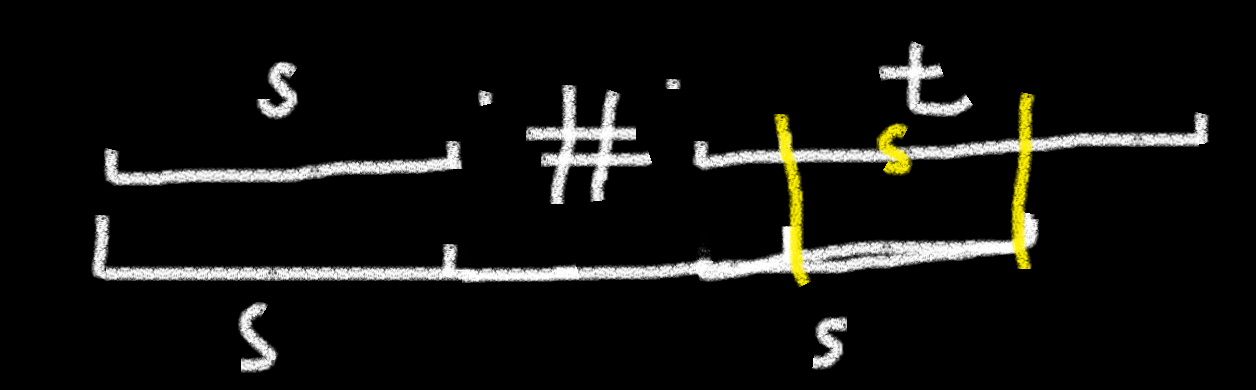
code

#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+6;
string s,t;
int p[N];
int main()
{
	cin>>t>>s;
	t=s+'#'+t;
	int len=t.length(),l=s.length();
	for(int i=1,j=0;i<len;i++)
	{
		while(t[i]!=t[j]&&j) j=p[j-1];
		p[i]=j+=(t[i]==t[j]);
		if(p[i]==l&&i!=l-1) printf("%d\n",i-2*l+1);
	}
	return 0;
}

Censoring

Trie树

Trie树，字典树，顾名思义，关于 “字典” 的一棵树，每个单词就是从根开始的一条路径。

如上面这棵字典树存了 \(ab.ac.acd.be\) 四个字符串。

板子大概长这样，注意数组往大了开，\(word\) 标记每个字符串的结尾，有时候可以计次数。

int cnt;
int son[MAX][26];
bool word[MAX];
void add(const string &x)
{
	int now=0,len=x.length();
	for(int i=0;i<len;i++)
	{
		int ch=x[i]-'a';
		if(!son[now][ch]) son[now][ch]=++cnt;
		now=son[now][ch];
	}
	word[now]=1;
}
bool que(const string &x)
{
	int now=0,len=x.length();
	for(int i=0;i<len;i++)
	{
		int ch=x[i]0-'a';
		if(!son[now][ch]) return 0;
		now=son[now][ch];
	}
	if(word[now]) return 1;
	else return 0;
}

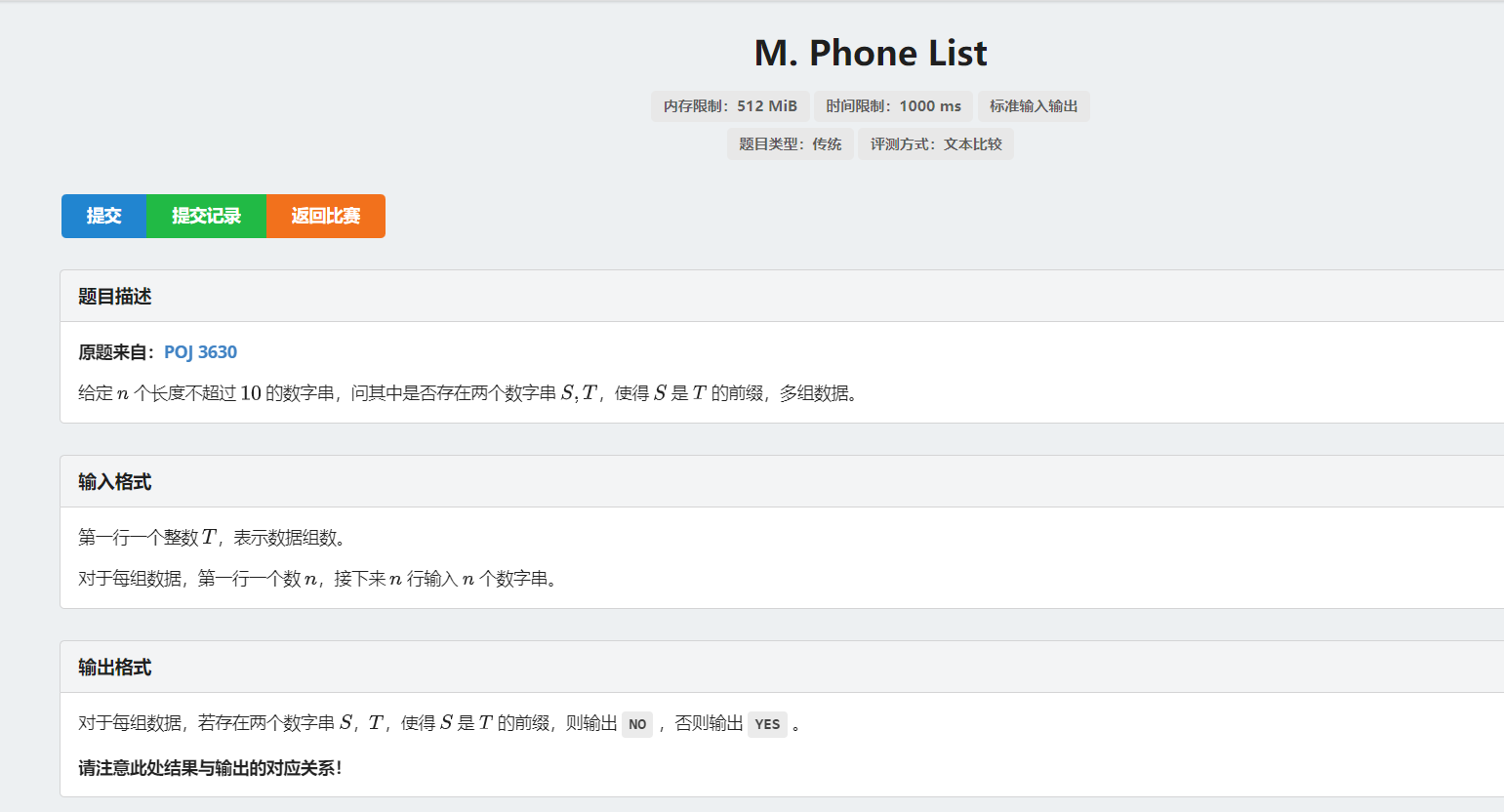
phone list

code

#include<bits/stdc++.h>
using namespace std;
const int N = 1e4+5;
string s[N];
int n,t,son[100005][10],tot;
bool word[N << 5];
bool add(const string &x)
{
	int num=tot;
	int now=0,len=x.length();
	for(int i=0;i<len;i++)
	{
		int ch=x[i]-'0';
		if(!son[now][ch]) son[now][ch]=++tot;
		now=son[now][ch];
		if(word[now]) return 1;
	}
	word[now]=1;
	return 0;
}
int main()
{
	scanf("%d",&t);
	while(t--)
	{
		memset(son,0,sizeof(son));
		memset(word,0,sizeof(word));

		tot=0;
		scanf("%d",&n);
		for(int i=1;i<=n;i++) cin>>s[i];
		sort(s+1,s+1+n);
		bool flag=1;
		for(int i=1;i<=n;i++)
		{
			if(add(s[i])) 
			{
				flag=0;
				printf("NO\n");
				break;
			}
		}
		if(flag) printf("YES\n");
	}
	return 0;
}

唐氏输出

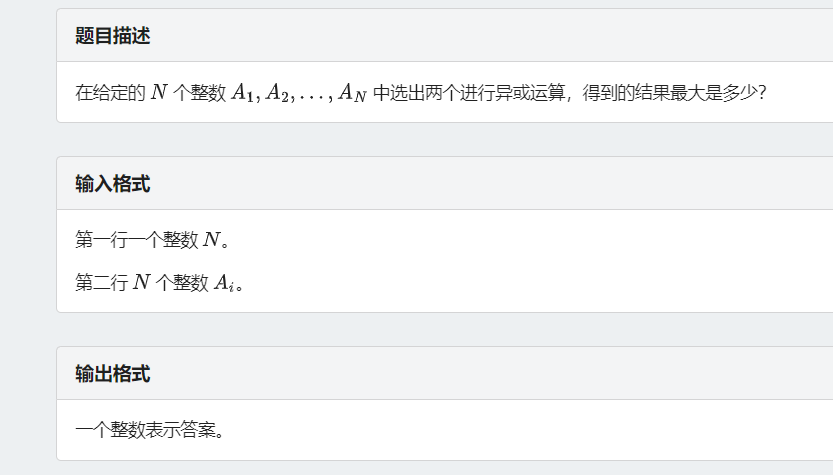
应用：最大异或和

Trie树用法很灵活，比较常用的是求最大异或和，

两个二进制数异或，不相同的位 越靠左 异或出来值越大，

所以我们贪心的想，从左往右遍历时，每一次都找与当前位不同的，这样最终肯定最大。

所以 01字典树 的原理就是这样。

The XOR Largest Pair

#include<bits/stdc++.h>
using namespace std;
const int N = 1e7+5;
int n;
int ans,y;
int son[N][2],tot;
bitset<32> x;
void mdf()
{
	int now=0;
	for(int i=31;i>=0;i--)
	{
		if(!son[now][x[i]]) son[now][x[i]]=++tot;
		now=son[now][x[i]];
	}
}
int que()
{
	int res=0,now=0;
	for(int i=31;i>=0;i--)
	{
		if(son[now][~x[i]]) res+=(1<<i),now=son[now][~x[i]];//尽量找 ~
		else now=son[now][x[i]];
	}
	return res;
}
int main()
{
	scanf("%d",&n);
	cin>>y; x=y; mdf();
	for(int i=2;i<=n;i++)
	{
		cin>>y; x=y;
		ans=max(que(),ans);
		mdf();
	}
	printf("%d\n",ans);
	return 0;
}

tips

异或有一个性质，就是 a^b^b=a ，所以可以想象成加减是一样的。

所以我们要求区间异或和可以用前缀和的形式，然后对 \(sum\) 数组跑01字典树。

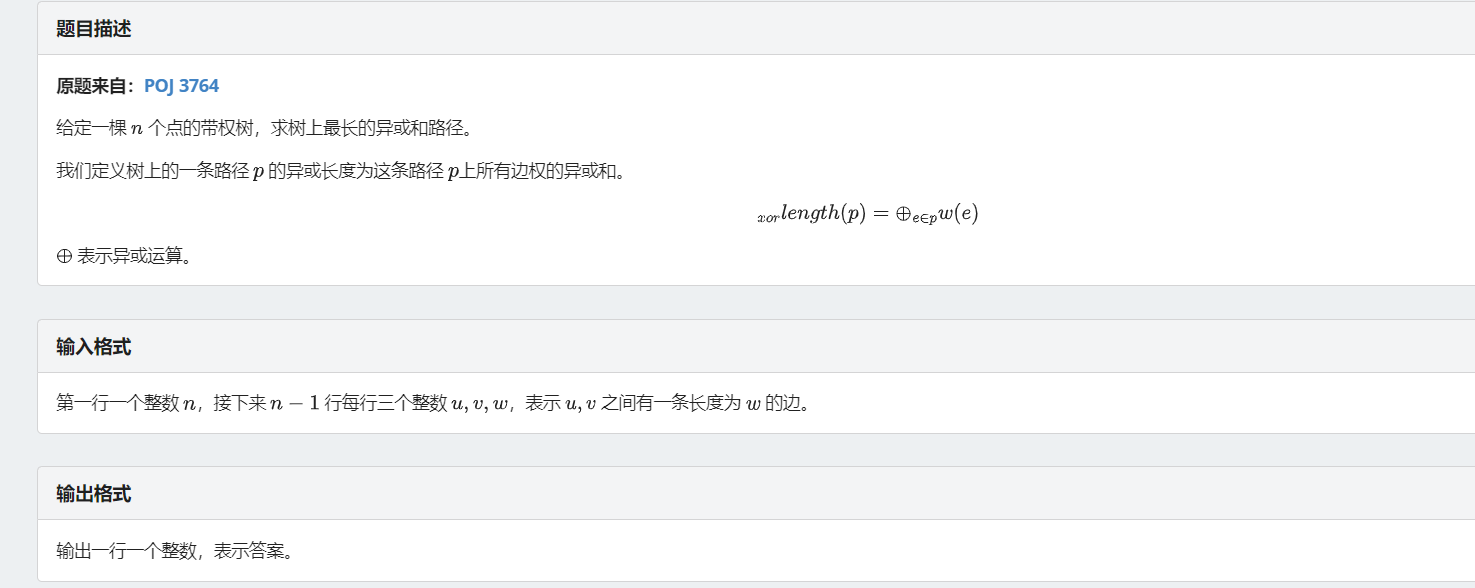
就是区间异或最大值，同样的原理可用于树上最长异或路径，

先 \(dfs\) 记录从根到每一个点的路径异或和，任意两个之间异或就是中间的一段路径。

The XOR-longest Path

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+5;
int n;
int head[N];
int tot,cnt;
bitset<32> p;
int son[10000005][2];
int ans;
void mdf()
{
	int now=0;
	for(int i=31;i>=0;i--)
	{
		if(!son[now][p[i]]) son[now][p[i]]=++cnt;
		now=son[now][p[i]];
	}
}
int que()
{
	int now=0,res=0;
	for(int i=31;i>=0;i--)
	{
		if(!son[now][~p[i]]) now=son[now][p[i]];
		else res+=(1<<i),now=son[now][~p[i]];
	}
	return res;
}
struct E
{
	int nxt,to,w;
} e[N << 1];
void add(int u,int v,int w)
{
	e[++tot]={head[u],v,w};
	head[u]=tot;
}
void dfs(int u,int d,int fa)
{
	for(int i=head[u];i;i=e[i].nxt) if(e[i].to!=fa)
	{
		dfs(e[i].to,d^e[i].w,u);
	}
	p=d;
	ans=max(ans,que());
	mdf();
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<n;i++)
	{
		int x,y,z;
		scanf("%d%d%d",&x,&y,&z);
		add(x,y,z); add(y,x,z);
	}
	dfs(1,0,0);
	printf("%d\n",ans);
	return 0;
}

Nikitosh 和异或

#include<bits/stdc++.h>
using namespace std;
const int N = 4e5+5;
int n,a[N],sum1[N],sum2[N];
int son[10000000][2],tot;
int dp1[N],dp2[N],ans;
bitset<32> p;
void add()
{
	int now=0;
	for(int i=31;i>=0;i--)
	{
		if(!son[now][p[i]]) son[now][p[i]]=++tot;
		now=son[now][p[i]];
	}
}
int que()
{
	int now=0,res=0;
	for(int i=31;i>=0;i--)
	{
		if(son[now][~p[i]]) res+=(1<<i),now=son[now][~p[i]];
		else now=son[now][p[i]];
	}
	return res;
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]),sum1[i]=sum1[i-1]^a[i];
	for(int i=n;i>=1;i--) sum2[i]=sum2[i+1]^a[i];
	add();
	for(int i=1;i<=n;i++)
	{
		dp1[i]=max(dp1[i-1],que());
		p=sum1[i];
		add();
	}
	p=0;
	memset(son,0,sizeof(son)); tot=0; add();
	for(int i=n;i>=1;i--)
	{
		dp2[i]=max(dp2[i+1],que());
		p=sum2[i];
		add();
	}
	for(int i=1;i<=n;i++) ans=max(ans,dp2[i]+dp1[i]);
	printf("%d\n",ans);
	return 0;
}

posted @ 2024-04-24 12:17 ppllxx_9G 阅读(14) 评论(0) 编辑收藏举报

刷新页面返回顶部

字符串基础：Hash，KMP，Trie树

Hash

注意

KMP

1.一些定义

2.前缀函数

1.暴力

2.优化一

3.优化二（成品）

KMP

Trie树

应用：最大异或和

tips

以下是博客签名，正文无关

公告