SPT
\(SPT(Super\ Piano\ Trick)\)
超级钢琴
选出 \(k\) 个最大的区间和,限制区间长度。
想到前缀和维护,然后区间最大值,可以确定每个左端点,对应的最大值。
维护前 \(k\) 大想到压堆,但是不可能全都压进去。
仍然是考虑对于每个左端点,右端点所在范围确定,那么当前的最大值就是确定的。
选完这个最大值,右端点所在范围中,当前选的这个点不能再选,其他的仍可能成为答案。
所以堆维护当前决策的区间和,最优决策点,左端点,以及右端点能取到的范围,每次相当于将右端点能取到的范围分成两部分,再找出最优决策压进去。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
#define mx(x,y) (a[x]>a[y]?x:y)
const int N = 5e5+5;
int n,a[N],L,R,k,st[40][N],lg[N];
LL ans;
struct A
{
int l,L,R,v,p;
bool operator < (const A &x) const {return v<x.v;}
};
priority_queue<A> q;
inline int get(int l,int r)
{
if(l>r) return -1;
int k=lg[r-l+1];
return mx(st[k][l],st[k][r-(1<<k)+1]);
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d%d%d",&n,&k,&L,&R); lg[0]=-1;
for(int i=1,x;i<=n;i++) scanf("%d",&x),a[i]=a[i-1]+x,st[0][i]=i,lg[i]=lg[i>>1]+1;
for(int i=1;i<=30;i++)
for(int j=1;j+(1<<i)-1<=n;j++)
st[i][j]=mx(st[i-1][j],st[i-1][j+(1<<(i-1))]);
for(int i=1;i<=n;i++)
{
if(i+L-1>n) break;
int l=i+L-1,r=min(n,i+R-1),p=get(l,r);
q.push({i,l,r,a[p]-a[i-1],p});
}
while(k)
{
A tmp=q.top(); q.pop();
ans+=tmp.v; k--;
int p1=get(tmp.L,tmp.p-1),p2=get(tmp.p+1,tmp.R);
if(tmp.L<=tmp.p-1) q.push({tmp.l,tmp.L,tmp.p-1,a[p1]-a[tmp.l-1],p1});
if(tmp.p+1<=tmp.R) q.push({tmp.l,tmp.p+1,tmp.R,a[p2]-a[tmp.l-1],p2});
}
printf("%lld\n",ans);
return 0;
}
异或粽子
只是把用 ST 表维护的区间最大值改成维护区间最大异或,用可持久化 Trie 维护。
注意可持久化 Trie 维护区间信息维护子树 size 有点麻烦,可以直接维护最靠右的出现位置,类扫描线的做法。
一般线性基维护区间信息也是类似。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 5e5+5;
int n,k;
LL a[N],ans;
namespace TRIE
{
int son[N<<6][2],mx[N<<6],rt[N],num;
inline void ins(LL x,int u,int lst)
{
rt[u]=++num;
int now=rt[u],now1=rt[lst];
for(int i=35;i>=0;i--)
{
int c=(x>>i)&1;
son[now][c]=++num;
son[now][c^1]=son[now1][c^1];
now=son[now][c]; now1=son[now1][c];
mx[now]=u;
}
}
inline int que(int a,int b,LL x)
{
if(b>a) return -1;
int now=rt[a];
for(int i=35;i>=0;i--)
{
int c=(x>>i)&1;
if(son[now][c^1]&&mx[son[now][c^1]]>=b) now=son[now][c^1];
else now=son[now][c];
}
return mx[now];
}
} using namespace TRIE;
struct A
{
int l,L,R,p; LL v;
inline bool operator < (const A &x) const {return v<x.v;}
};
priority_queue<A> q;
inline LL read()
{
LL res=0; char x=getchar();
while(x<'0'||x>'9') x=getchar();
while(x>='0'&&x<='9') res=(res<<1)+(res<<3)+(x^48),x=getchar();
return res;
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
n=read(); k=read();
for(int i=1;i<=n;i++)
{
a[i]=a[i-1]^read();
ins(a[i],i,i-1);
}
for(int i=1;i<=n;i++)
{
int p=que(n,i,a[i-1]);
q.push({i,i,n,p,a[p]^a[i-1]});
}
while(k)
{
A tmp=q.top(); q.pop();
ans+=tmp.v; k--;
int p1=que(tmp.R,tmp.p+1,a[tmp.l-1]),p2=que(tmp.p-1,tmp.L,a[tmp.l-1]);
if(p2!=-1) q.push({tmp.l,tmp.L,tmp.p-1,p2,a[p2]^a[tmp.l-1]});
if(p1!=-1) q.push({tmp.l,tmp.p+1,tmp.R,p1,a[p1]^a[tmp.l-1]});
}
printf("%lld\n",ans);
return 0;
}
\(kth\)
序列合并
应该是这类题最简单的,但思路很通用。
开优先队列直接记,注意重复的状态需要标记,因为只有两个数组,所以每个后继状态只会有两个,暴力加入就行。
下面的题就是在处理后继状态很多的情况。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 1e5+5;
unordered_map<int,bool> mp[N];
int n,a[N],b[N],m;
struct A
{
int a,b,sum;
inline bool operator < (const A &x) const {return sum>x.sum;}
};
priority_queue<A> q;
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&n); m=n;
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<=n;i++) scanf("%d",&b[i]);
sort(a+1,a+1+n); sort(b+1,b+1+n);
q.push({1,1,a[1]+b[1]}); mp[1][1]=1;
while(m)
{
A tmp=q.top(); q.pop();
printf("%d ",tmp.sum); m--;
if(!mp[tmp.a+1][tmp.b]) q.push({tmp.a+1,tmp.b,a[tmp.a+1]+b[tmp.b]}),mp[tmp.a+1][tmp.b]=1;
if(!mp[tmp.a][tmp.b+1]) q.push({tmp.a,tmp.b+1,a[tmp.a]+b[tmp.b+1]}),mp[tmp.a][tmp.b+1]=1;
}
return 0;
}
Robotic Cow Herd P
加强版,给 \(m\) 个数组,求前 \(k\) 大方案和。
发现每个状态最多有 \(m\) 个后继状态,考虑如何减少后继状态(实际上是将后继状态排个序,然后按次序加进去)。
有一种很好的转移方法:
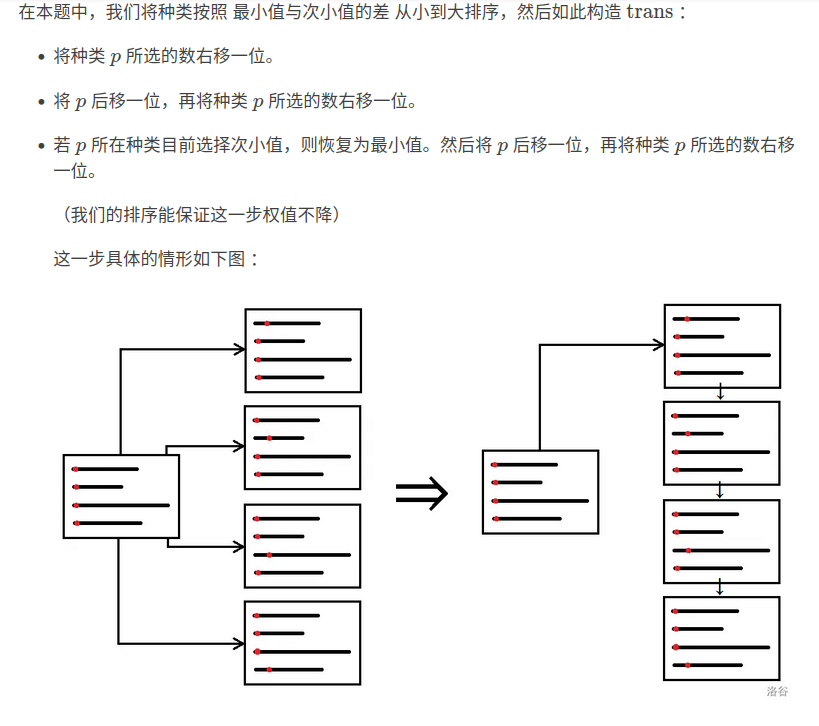
图片来自 题解 【P6646 [CCO2020] Shopping Plans】,讲的真的很好。
通过钦定当前的操作组,实现转移的定向。按差值排序保证了恢复操作也满足后继状态一定比当前状态更劣。
很巧妙,尤其是将当前组恢复为最优状态,然后再改变下一组的操作。保证不重不漏。
据说还可以图论建模,跑分层 \(k\) 短路。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 1e5+5;
int n,m[N],k;
vector<int> p[N];
struct A
{
int x,y; LL sum;
inline bool operator < (const A &x) const {return sum>x.sum;}
};
priority_queue<A> q;
LL ans;
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
LL sum=0;
scanf("%d%d",&n,&k); int cnt=0;
for(int i=1;i<=n;i++)
{
scanf("%d",&m[i]);
if(m[i]==1) {scanf("%d",&m[i]); sum+=m[i]; continue;}
p[++cnt].resize(m[i]);
for(int &j:p[cnt]) scanf("%d",&j);
}
n=cnt;
for(int i=1;i<=n;i++)
{
sort(p[i].begin(),p[i].end());
}
sort(p+1,p+1+n,[&](const vector<int> &x,const vector<int> &y){return (x.size()>1&&y.size()>1)?(x[1]-x[0]<y[1]-y[0]):(0);});
for(int i=1;i<=n;i++) sum+=p[i][0];
ans+=sum; k--;
q.push({1,1,sum-p[1][0]+p[1][1]});
while(!q.empty()&&k)
{
A tmp=q.top(); q.pop();
ans+=tmp.sum; k--;
if(tmp.y==1&&tmp.x<n) q.push({tmp.x+1,1,tmp.sum+p[tmp.x+1][1]-p[tmp.x+1][0]+p[tmp.x][0]-p[tmp.x][1]});
if(tmp.y<p[tmp.x].size()-1) q.push({tmp.x,tmp.y+1,tmp.sum-p[tmp.x][tmp.y]+p[tmp.x][tmp.y+1]});
if(tmp.x<n) q.push({tmp.x+1,1,tmp.sum-p[tmp.x+1][0]+p[tmp.x+1][1]});
}
printf("%lld\n",ans);
return 0;
}
Shopping Plans
大杂烩,好多 trick。
总结一下 spt(实际上就是前 \(k\) 优问题)。
当 \(k\) 较小时,我们考虑将最优状态(\(S\))加入优先队列,然后依次将次优的状态加入,可以将这些次优状态称为后继状态(\(trs(S)\))。
如果从 \(S\) 向 \(trs(S)\) 连边,就能得到一棵以最优状态为根的外向树,易证前 \(k\) 优就是包含根的大小为 \(k\) 的连通块。
关键就在于如何减少后继状态。
“减少”其实并不准确,我们只需要将原来很多个 \(trs(S)\) 排出次序,每次仍加入最优的几个,就能减少每一个状态的后继(菊花转链)。
(如果 \(k\) 较大,考虑树上二分等。)
Multiset
在可重正整数集 \(S\) 中选出大小为 \([l,r]\) 的子集,求前 \(k\) 小的子集和。
容易确定最优状态,就是排完序选前 \(l\) 个。
朴素转移就是对于每一个元素,找到下一个比它大的(不能和右边的有重合),然后指针右移。
这样最多会有 \(r\) 个后继状态,不可接受。
我们可以通过多记录几个状态,进行单向的转移。
即从最右边的元素开始(最开始只能移动这一个),将这个作为操作元素,转移有三种:
-
移动操作元素——指针右移。
-
将操作元素 定位为下一个(左边),移动操作元素——指针右移。
-
从 \(l\) 个元素扩展到 \(l+1\) 个元素。
记录 \(x\) 表示上一个元素的位置,\(y\) 表示当前的操作元素,\(z\) 表示下一个。
这样就可以按顺序的访问所有后继状态,并且最多有三个儿子。
Arrays
\(m\) 个数组,每个数组中选一个,求前 \(k\) 小和。
思路类似,具体实现请看例题
Shopping Plans
如果你做完上面两个问题,你发现这道题就是把两个问题揉一起了。
对于每一组内用 \(Arrays\) 的方法求组内前 \(k\) 小,这个对于每一组都是完全独立的。
可以利用这个 "黑盒"(好形象)做 \(Multiset\),然后就做完了。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 2e5+5;
const LL inf = 1e18+5;
int n,m,k,t[N];
struct Mul
{
int l,r;
struct A
{
int x,y,z; LL sum;
inline bool operator < (const A &x) const {return sum>x.sum;}
};
priority_queue<A> q;
vector<LL> a,c;
inline void kth(int k)
{
if(k<(int)a.size()) return ;
if(q.empty()) {a.push_back(inf); return;}
A tmp=q.top(); q.pop();
int x=tmp.x,y=tmp.y,z=tmp.z; LL s=tmp.sum;
a.push_back(s);
if(z==(int)c.size()-1&&x+1==y&&y+1<r) q.push({x+1,y+1,z,s+c[y+1]});
if(y>=0&&y+1<=z) q.push({x,y+1,z,s-c[y]+c[y+1]});
if(x>=0&&x+1<=y-1) q.push({x-1,x+1,y-1,s+c[x+1]-c[x]});
}
inline void init()
{
sort(c.begin(),c.end());
if(l>(int)c.size()) {a.push_back(inf); a.push_back(inf); return;}
r=min<int>(r,c.size());
LL sum=0;
for(int i=0;i<l;i++) sum+=c[i];
q.push({l-2,l-1,(int)c.size()-1,sum});
kth(0); kth(1);
}
} a[N];
struct A
{
int x,y; LL s;
inline bool operator < (const A &x) const {return s>x.s;}
};
priority_queue<A> q;
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d%d",&n,&m,&k);
for(int i=1;i<=n;i++)
{
int a,c; scanf("%d%d",&a,&c);
::a[a].c.push_back(c);
} LL sum=0;
for(int i=1;i<=m;i++)
{
scanf("%d%d",&a[i].l,&a[i].r),a[i].init();
sum+=a[i].a[0]; sum=min(sum,inf); t[i]=i;
}
sort(t+1,t+1+m,[&](const int &x,const int &y){return a[x].a[1]-a[x].a[0]<a[y].a[1]-a[y].a[0];});
if(sum<inf)
{
printf("%lld\n",sum); k--;
q.push({1,1,sum-a[t[1]].a[0]+a[t[1]].a[1]});
}
while(k&&!q.empty())
{
A tmp=q.top(); q.pop();
int x=tmp.x,y=tmp.y; LL s=tmp.s;
if(s>=inf) break;
printf("%lld\n",s); k--;
if(x<m&&y==1) q.push({x+1,1,s-a[t[x]].a[1]+a[t[x]].a[0]-a[t[x+1]].a[0]+a[t[x+1]].a[1]});
if(x<m) q.push({x+1,1,s-a[t[x+1]].a[0]+a[t[x+1]].a[1]});
a[t[x]].kth(y+1);
q.push({x,y+1,s-a[t[x]].a[y]+a[t[x]].a[y+1]});
}
while(k) printf("-1\n"),k--;
return 0;
}



