DFS序、倍增、ST表、LCA

dfs序

\(dfs\) 序用于树状结构，顾名思义，就是在 \(dfs\) 过程中为每个点打上标记，每个点会被标记两次（第一次搜到和回溯时），

可以分别记为 \(in[u]\) , \(out[u]\) 。这样可以将一棵子树用一段区间表示（把树“拍”在线段上）。

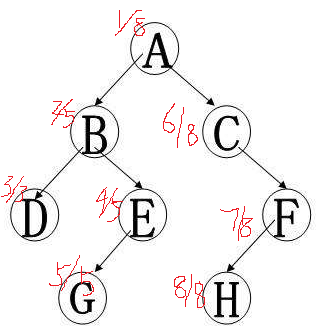
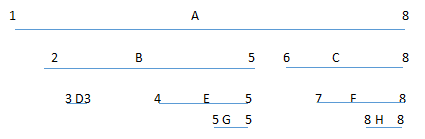
于是一棵树就被压扁成区间了，线段树，树状数组，st表 …… 对区间进行维护的都可以用啦。

(例： [POI2007] MEG-Megalopolis，注意边权转点权）

void dfs(int u)
{
	in[u]=++cnt;
	for(int i=head[u];i;i=e[i].nxt)
	{
		int v=e[i].to;
		if(in[v]) continue;
		dfs(v);
	}
	out[u]=cnt;
}

st表

维护区间最值， \(O(nlogn)\) 预处理， \(O(1)\) 查询，不支持修改。

有点类似树状数组， \(st[i][j]\) 表示以 \(i\) 为起点，长度为 \(2^j\) 的区间最值，

可以由 \(st[i][j-1],st[i+(1<<(j-1))][j-1]\) 转移。

struct ST
{
	int st[30][N];
	void bui()
	{
		for(int i=1;i<=n;i++) st[0][i]=a[i];
		for(int i=1;i<=25;i++) 
			for(int j=1;j+(1<<i)-1<=n;j++)
				st[i][j]=max(st[i-1][j],st[i-1][j+(1<<i-1)]);
	}
	int que(int l,int r)
	{
		int k=__lg(r-l+1);
		return max(st[k][l],st[k][r-(1<<k)+1]);
	}
} st;

LCA

最近公共祖先，先维护每个节点的深度，用倍增的思想，两个点同时向上跳。

（注意：如果图不是树，可以用最小/大生成树建树）

int lca(int x,int y){
	if(dep[x]<dep[y]) swap(x,y);
	int d=dep[x]-dep[y];
	for(int i=0;i<30;i++) if(d&(1<<i)) x=f[x][i];//先跳到同一深度
	if(x==y) return x;
	for(int i=29;i>=0;i--)//倒序循环，防止跳多。
	{
		if(f[x][i]!=f[y][i])
		{
			x=f[x][i]; y=f[y][i];//一起跳
		}
	}
	return f[x][0];
}

换根（参考dfs序）

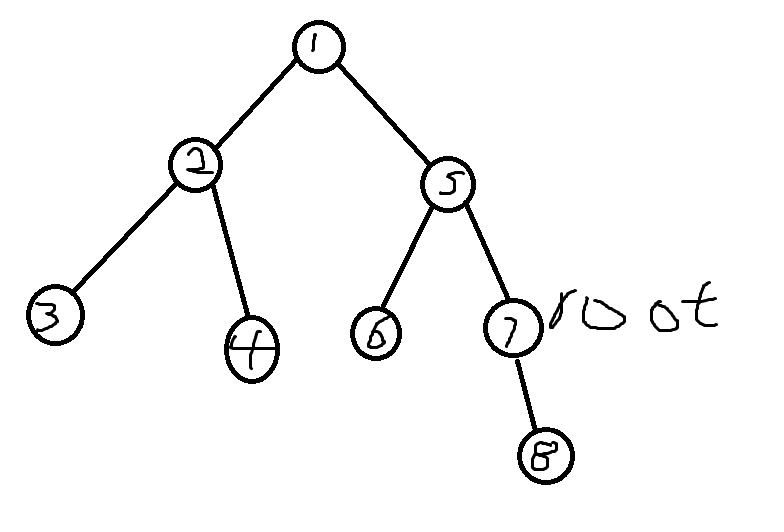
考虑三种情况
首先 \(dfs\)序 ，把树压成区间。如上图，根节点从 \(1\) 变为 \(7\)。

考虑三种情况：

• 查询节点为当前根节点的子节点，不会受影响，查询区间不变；(如 \(8\)）

• 查询节点与当前根节点属于两棵子树，也不会受影响，查询区间不变；（如 \(2\)）

• 查询节点（\(x\)）为当前根节点的祖先（如 \(1\)），先从根往上找，找到 \(x\) 下面的一个点（用 \(lca\)），
  这个点就是它的祖先,查询除了这个点的子树外其他的部分。

题目描述

code

#include<bits/stdc++.h>
using namespace std;
#define ls (rt << 1)
#define rs (rt << 1 | 1)
const int N = 100005 , M = 100005;
int st[N][40],a[N];
int n,m,root;
int head[N],tot;
struct E
{
	int nxt,to;
} e[M*2];
struct T
{
	int l,r,mi;
} tr[N << 2];
void pushup(int rt)
{
	tr[rt].mi=min(tr[ls].mi,tr[rs].mi);
}
void bui(int rt,int l,int r)
{
	tr[rt]={l,r};
	if(l==r) return;
	int mid=(l+r) >> 1;
	bui(ls,l,mid); bui(rs,mid+1,r);
}
void mdf(int rt,int x,int v)
{
	if(tr[rt].l==tr[rt].r)
	{
		tr[rt].mi=v;
		return;
	}
	int mid=(tr[rt].l+tr[rt].r)>>1;
	if(x<=mid) mdf(ls,x,v);
	if(x>mid) mdf(rs,x,v);
	pushup(rt);
}
int que(int rt,int l,int r)
{
	if(l<=tr[rt].l&&r>=tr[rt].r)
		return tr[rt].mi;
	int mid=(tr[rt].l+tr[rt].r)>>1;
	int res=1e9;
	if(l<=mid) res=min(res,que(ls,l,r));
	if(r>mid) res=min(res,que(rs,l,r));
	return res;
}
void add(int u,int v)
{
	e[++tot]={head[u],v};
	head[u]=tot;
}
int dep[N],in[N],out[N],cnt;
void dfs(int u,int fa)
{
	dep[u]=dep[fa]+1;
	st[u][0]=fa;
	in[u]=++cnt;
	for(int i=head[u];i;i=e[i].nxt)
	{
		int v=e[i].to;
		if(v==fa) continue;
		dfs(v,u);
	}
	out[u]=cnt;
}
int lca(int x,int y)
{
	if(dep[x]<dep[y]) swap(x,y);
	for(int i=30;i>=0;i--)
		if(dep[st[x][i]]>dep[y]) x=st[x][i];
	return x;
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		if(x==0) a[i]=y;
		else add(x,i),add(i,x),a[i]=y;
	}
	root=1;
	dfs(1,0);
	for(int i=1;i<=30;i++)
		for(int j=1;j<=n;j++)
			st[j][i]=st[st[j][i-1]][i-1];
	bui(1,1,cnt);
	for(int i=1;i<=n;i++) mdf(1,in[i],a[i]);
		
	for(int i=1;i<=m;i++)
	{
		string c;
		int x,y;
		cin>>c;
		if(c[0]=='E')
		{
			scanf("%d",&x);
			root=x;
		}
		else if(c[0]=='V')
		{
			scanf("%d%d",&x,&y);
			mdf(1,in[x],y);
		}
		else
		{
			scanf("%d",&x);
			if(x==root) printf("%d\n",que(1,1,cnt));
			else if(in[x]<=in[root]&&out[x]>=in[root])
			{
				int k=lca(x,root);
				printf("%d\n",min(que(1,1,in[k]-1),que(1,out[k]+1,cnt)));
			}	
			else printf("%d\n",que(1,in[x],out[x]));
		}	
	}
	return 0;
}