tarjan 及圆方树
强连通分量 SSC (缩点)
有向图缩点(把一个强连通分量看成一个点),用于优化。
-
树枝边:DFS 时经过的边,即 DFS 搜索树上的边
-
反祖边:也叫回边或后向边,与 DFS 方向相反,从某个结点指
向其某个祖先的边 -
横叉边:从某个结点指向搜索树中另一子树中的某结点的边,它
主要是在搜索的时候遇到了一个已经访问过的结点,但是这个结
点并不是当前结点的祖先时形成的 -
前向边:与 DFS 方向一致,从某个结点指向其某个子孙的边,
它是在搜索的时候遇到子树中的结点的时候形成的
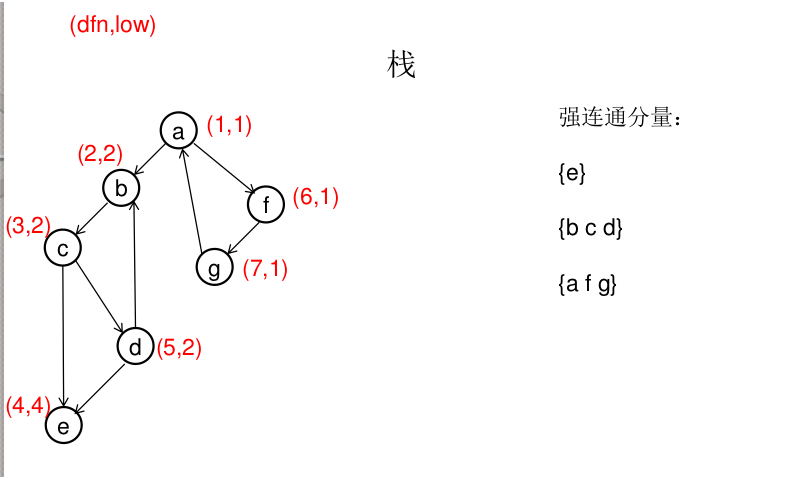
对于每个点维护两个值 \((dfn,low)\) ,\(dfn\) 是 dfs 序,\(low\) 表示这条路走到头能回到祖宗的最小值(或叶子)。
对于一个点 \(u\) ,如果他的 \(low_u\) 等于 \(dfn_u\) ,说明 向下 dfs 时还能回到 \(u\) ,则中间这部分构成一个强连通分量。
如图,先 dfs 到 \(e\) ,dfn[e]==low[e],发现一个强连通分量,\(e\) 出栈,回溯到 \(b\) ,第二个强连通分量,将 \(b,c,d\) 出栈。
缩完点变成有向无环图(DAG),可以跑最短路,可以 dp,很方便。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 10005,M = 100005;
int n,m;
int head[N],tot;
struct E {int u,v;} e[M<<1];
inline void add(int u,int v) {e[++tot]={head[u],v}; head[u]=tot;}
int dfn[N],num,low[N],bl[N],cnt,top,st[N];
vector<int> scc[N];
bool vs[N];
void tj(int u)
{
dfn[u]=low[u]=++num; vs[u]=1;
st[++top]=u;
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v;
if(!dfn[v])
{
tj(v);
low[u]=min(low[u],low[v]);
}
else if(vs[v])
low[u]=min(low[u],dfn[v]);
}
if(dfn[u]==low[u])
{
++cnt; int now;
do
{
now=st[top--]; vs[now]=0;//注意出栈清空标记
bl[now]=cnt; scc[cnt].push_back(now);
} while(now!=u);
}
}
bool ans[N];
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int x,y; scanf("%d%d",&x,&y);
add(x,y);
}
for(int i=1;i<=n;i++) if(!dfn[i]) tj(i);
printf("%d\n",cnt);
for(int i=1;i<=n;i++)
{
int k=bl[i]; if(ans[k]) continue;
sort(scc[k].begin(),scc[k].end());
for(int j:scc[k]) printf("%d ",j); putchar('\n');
ans[k]=1;
}
return 0;
}
割点
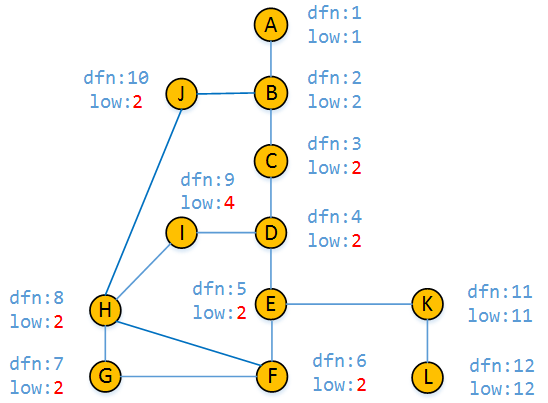
无向图求割点,就是删掉后能把图割成几个部分的点,思路和缩点类似,如果 dfn[u]<=low[v] ,说明 \(u\) 以下有一个连通块,且 \(u\) 下面的连通块和 \(u\) 上面的没有联系,所以此时 \(u\) 为割点。
如图 \(B,E,K\) 为割点。
(注意,根节点如果只有一个儿子,他不是割点。)
code
void tj(int s)
{
dfn[s]=low[s]=++num;
int son=0;
for(int i=head[s];i;i=e[i].nxt)
{
int to=e[i].to;
if(!dfn[to])
{
tj(to);
low[s]=min(low[s],low[to]);
if(dfn[s]<=low[to])
{
son++;
if(s!=root || son>1)
{
if(!ans[s]) cnt++;
ans[s]=1;
}
}
}
else
low[s]=min(low[s],dfn[to]);
}
}
割边
无向图求割边,定义和割点差不多。
如 dfn[u]<low[v] 则 \((u,v)\) 为割边(注意不能 \(=\) ),上图割边有 \(A-B\) 以及 \(E-K\) 和 \(K-L\),因为是无向图,建边时都建成了正向反向两条边,所以要判一下正向反向的两条边,避免原路走回去。
code
void tj(int s,int fa)
{
dfn[s]=low[s]=++num;
for(int i=head[s];i;i=e[i].nxt)
{
int to=e[i].to;
if(to==fa) continue;
if(!dfn[to])
{
tj(to,s);
low[s]=min(low[s],low[to]);
if(dfn[s]<low[to]) ans++;
}
else low[s]=min(low[s],dfn[to]);
}
}
点双连通分量
如果一个无向图中删掉任意一个点后图仍连通,则称这个图 “点双连通” ,点双连通分量就是能找到的 “极大” 的点双连通的子图(任意再加一个点都不行)。
割点的会把图割成几个连通块,这些连通块一定满足点双,但不完整,因为与它相邻的割点处于连通块边缘,如果加进连通块也可以(当叶子),所以同一个割点可能同属于好几个点双,不能用 \(color\) 标记,要用数组存一下。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5+5,M = 2e6+5;
int n,m;
int head[N],tot;
struct E {int u,v;} e[M<<1];
inline void add(int u,int v) {e[++tot]={head[u],v}; head[u]=tot;}
int dfn[N],low[N],num,st[N<<1],top,rt,cnt;
vector<int> vcc[N<<1];
void tj(int u)
{
dfn[u]=low[u]=++num;
st[++top]=u;
int son=0;
if(u==rt&&!head[u])//特判单点
{
vcc[++cnt].push_back(u); return;
}
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v;
if(!dfn[v])
{
tj(v);
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u])//注意要确定到 v,因为一个 u 可能被算很多次。
{
son++;
cnt++; int now;
do
{
now=st[top--]; vcc[cnt].push_back(now);
} while(now!=v);//注意是不等于儿子
vcc[cnt].push_back(u);//加入父亲
}
}
else low[u]=min(low[u],dfn[v]);
}
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d",&n,&m);
if(n==1)
{
printf("1\n1 1\n"); return 0;
}
for(int i=1;i<=m;i++)
{
int x,y; scanf("%d%d",&x,&y);
if(x==y) continue;//注意自环,会出问题
add(x,y); add(y,x);
}
for(int i=1;i<=n;i++) if(!dfn[i]) rt=i,tj(i);
printf("%d\n",cnt);
for(int i=1;i<=cnt;i++)
{
printf("%d ",vcc[i].size());
for(int j:vcc[i]) printf("%d ",j); putchar('\n');
}
return 0;
}
边双连通分量
定义和点双类似,去掉任意一条边仍连通的极大子图,求法和 SSC 缩点有点像,只需要判重边就行了(见求割边)。
边双满足任意两点之间一定存在两条完全没有重复部分的路(如果有重复部分,割掉就断了)。
直接套强连通分量的板子就行,注意必须传边防止重边。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5+5,M = 2e6+6;
int n,m;
int head[N],tot=1;
struct E {int u,v;} e[M<<1];
inline void add(int u,int v) {e[++tot]={head[u],v}; head[u]=tot;}
int dfn[N],low[N],num,st[N],top,cnt;
vector<int> ecc[N];
void tj(int u,int ed)//防止有重边,必须传边,为了方便对应 tot=1,有点像网络流
{
dfn[u]=low[u]=++num;
st[++top]=u;
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v;
if(!dfn[v])
{
tj(v,i);
low[u]=min(low[u],low[v]);
}
else if(i!=(ed^1)) low[u]=min(low[u],dfn[v]);
}
if(low[u]==dfn[u])//跟SSC一模一样
{
++cnt; int now;
do
{
now=st[top--]; ecc[cnt].push_back(now);
} while(now!=u);
}
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int x,y; scanf("%d%d",&x,&y);
add(x,y),add(y,x);
}
for(int i=1;i<=n;i++) if(!dfn[i]) tj(i,-1);
printf("%d\n",cnt);
for(int i=1;i<=cnt;i++)
{
printf("%d ",ecc[i].size());
for(int j:ecc[i]) printf("%d ",j); putchar('\n');
}
return 0;
}
注意
板子别打错!!!
update:2024.9.30 更新了代码,微调排版。
圆方树
一直以为自己没学会,直到做题的时候突然糊出来一个类似的东西,然后死去的回忆突然开始攻击我……
圆方树,对于无向图建立的树形结构,用于解决有关点双连通分量的问题。
具体构建方法:将每个点双连通分量建立一个虚点(方点),点双里面的实点(圆点)按菊花形连在虚点上。
可以把图上的问题转化为树上的问题,两点之间必须经过的点就是树上路径经过的实点。
例题:压力
一开始想建 dfn 树然后返祖边覆盖,覆盖到的不会被贡献,然后发现其实对于所有点双都有这个性质,也就是我们只关心割点。
问题变成对路径上所有割点做贡献,然后缩点就可以做了,但是很麻烦吧。
这个图就已经很像圆方树了,能自然的想到对每个点双开一个虚点,然后让点环绕它,那么路径就只会经过 割点——虚点——割点,这就是我们想要的。
然后你就发明了圆方树了。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
#define fi first
#define se second
const int N = 2e5+5,M = 4e5+5;
int n,m,Q;
int head[N],tot=1;
struct E {int u,v;} e[M<<1];
inline void add(int u,int v) {e[++tot]={head[u],v}; head[u]=tot;}
int dfn[N],low[N],num,sta[N],top,cnt;
vector<int> g[N];
void tj(int u)
{
dfn[u]=low[u]=++num; sta[++top]=u;
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v;
if(!dfn[v])
{
tj(v);
low[u]=min(low[u],low[v]);
if(low[v]==dfn[u])
{
++cnt; int now;
do
{
now=sta[top--];
g[cnt].push_back(now); g[now].push_back(cnt);
} while(now!=v);
g[cnt].push_back(u); g[u].push_back(cnt);
}
}
else low[u]=min(low[u],dfn[v]);
}
}
int d[N],st[30][N],lg[N],fa[N];
void dfs(int u,int f)
{
dfn[u]=++num; st[0][num]=f; fa[u]=f;
for(int v:g[u])
{
if(v==fa[u]) continue;
dfs(v,u);
}
}
#define mi(x,y) (dfn[x]<dfn[y]?x:y)
inline int get(int x,int y)
{
if(x==y) return x;
if((x=dfn[x])>(y=dfn[y])) swap(x,y); x++;
int k=lg[y-x+1];
return mi(st[k][x],st[k][y-(1<<k)+1]);
}
void sol(int u)
{
for(int v:g[u])
{
if(v==fa[u]) continue;
sol(v);
d[u]+=d[v];
}
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d%d",&n,&m,&Q);
for(int i=1;i<=m;i++)
{
int x,y; scanf("%d%d",&x,&y);
add(x,y); add(y,x);
}
cnt=n;
for(int i=1;i<=n;i++) if(!dfn[i]) tj(i);
num=0; lg[0]=-1;
for(int i=1;i<=cnt;i++) dfn[i]=0,lg[i]=lg[i>>1]+1;
dfs(1,0);
for(int i=1;i<=20;i++) for(int j=1;j+(1<<i)-1<=cnt;j++) st[i][j]=mi(st[i-1][j],st[i-1][j+(1<<(i-1))]);
while(Q--)
{
int x,y,z; scanf("%d%d",&x,&y); z=get(x,y);
d[x]++; d[y]++; d[z]--; d[fa[z]]--;
}
sol(1);
for(int i=1;i<=n;i++) printf("%d\n",d[i]);
return 0;
}
顺便找到了已经死去的圆方树学习笔记,只写了两句话,放这里了,纪念我死去的暑假。
圆方树
感谢学长的馈赠)
点双连通子图:任意两个点间至少存在两条点不重复的路径。
点双连通分量:一个极大的点双连通子图。
圆方树其实就是将每个点双作为方点,点双内部的点作为原点连接在方点上。
因为割点至少会在两个点双中,所以每两个方点之间由割点相连。(方点可以理解为一个虚拟的点)
任意一个点双中的两个点一定有至少两条点不重复的路径。
update:2025.1.14


 浙公网安备 33010602011771号
浙公网安备 33010602011771号