山海经（线段树）

山海经

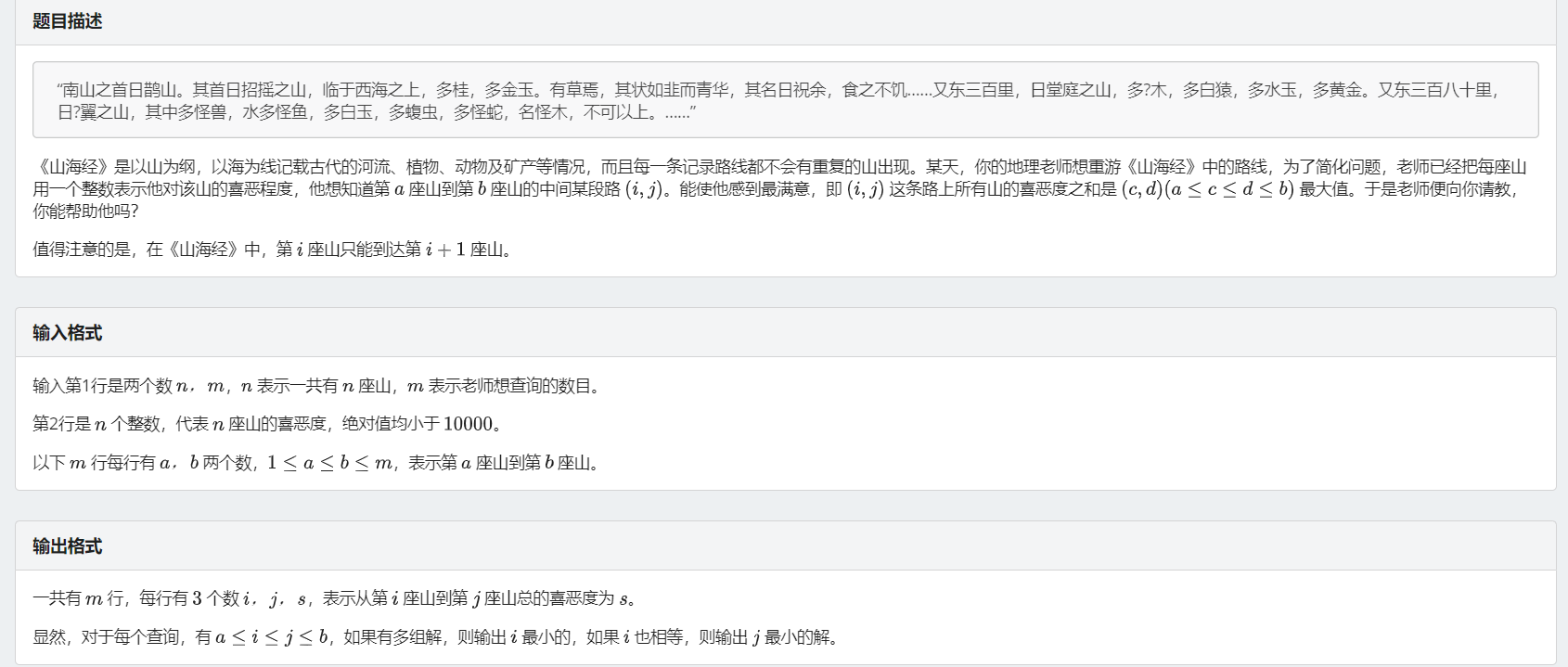
题目描述

样例

输入

5 3
5 -6 3 -1 4
1 3
1 5
5 5

输出

1 1 5
3 5 6
5 5 4

题目大意

输入一个区间，求它所有子区间和的最大值。

题解

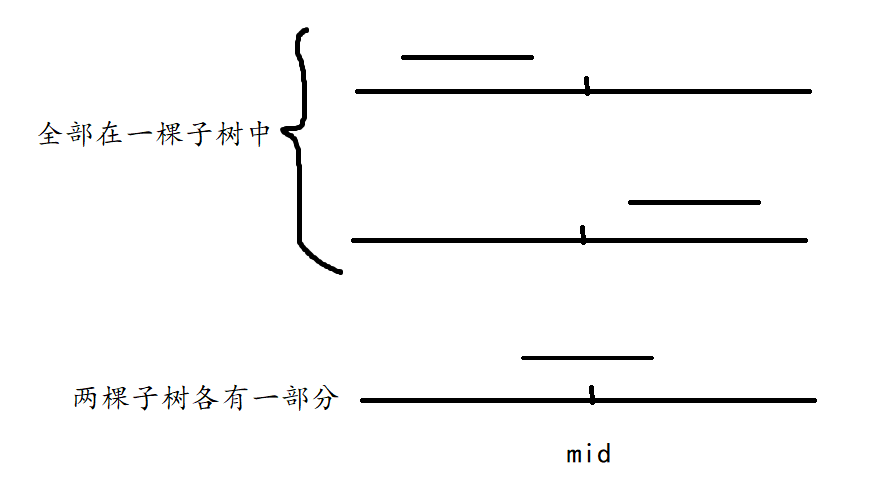
对于每一个区间 \(L~R\) 的最优解 \(i~j\) ，只有三种可能：

• 一 全部在左子树中

• 二 正好跨过中点，左子树右子树中都有一部分

• 三 全部在右子树中

对于全部在子树中的情况，简单，直接递归查询。

难点在中间卡住的情况，不能找子区间再求和，那就直接从最优解出发，这个解就是一个区间和，由左右两部分组成，既然是最优解，那左右两部分一定也满足是最优，即左子树的最优后缀和和右子树的最优前缀和相加（也有可能是子树再向下递归时返回值）。

所以用线段树维护区间最优前缀和及端点，最优后缀和及端点，区间和，区间最优解，左右端点。

合并时前缀和为 左子树的前缀和 或 左子树的全部加上右子树的前缀和，后缀和同理，最优解合并见上文。

code

#include<bits/stdc++.h>
using namespace std;
#define ls (rt << 1)
#define rs (rt << 1 | 1)
#define lll long long
const int N = 100005;
const int M = (1e9);
int n,m,a[N];
int ww=-1;
struct T
{
	int l,r,data,qz,hz,q,h,ans,ansl,ansr;
}tr[N<<2];

T pushup(T rt1,T rt2)
{
	T tree;
	tree.data=rt1.data+rt2.data;
	tree.l=rt1.l; tree.r=rt2.r;
	if (rt1.q<rt1.data+rt2.q)
	{
		tree.q=rt1.data+rt2.q;
		tree.qz=rt2.qz;
	}
	else {tree.q=rt1.q; tree.qz=rt1.qz;}
	if (rt2.h<=rt2.data+rt1.h) 
	{
		tree.h=rt2.data+rt1.h; 
		tree.hz=rt1.hz;
	}
	else {tree.h=rt2.h; tree.hz=rt2.hz;}

	tree.ans=rt1.ans; 
	tree.ansl=rt1.ansl; 
	tree.ansr=rt1.ansr;//先选左边，附初始值。
	if(rt1.h+rt2.q>tree.ans)
	{
		tree.ans=rt1.h+rt2.q; 
		tree.ansl=rt1.hz; 
		tree.ansr=rt2.qz;
	}
	if(rt2.ans>tree.ans)
	{
		tree.ans=rt2.ans; 
		tree.ansl=rt2.ansl; 
		tree.ansr=rt2.ansr;
	}
	return tree;
}
void bui(int rt,int l,int r)
{
	tr[rt].l=l; tr[rt].r=r;
	if(l==r)
	{
		tr[rt].qz=tr[rt].hz=tr[rt].ansl=tr[rt].ansr=l;
		tr[rt].data=tr[rt].q=tr[rt].h=tr[rt].ans=a[l];
		return;
	}
	int mid=((lll)l+r)>>1;
	bui(ls,l,mid); 
	bui(rs,mid+1,r);
	tr[rt]=pushup(tr[ls],tr[rs]);
}
T que(int rt,int l,int r)
{
	if(l<=tr[rt].l&&r>=tr[rt].r) return tr[rt];
	int mid=((lll)tr[rt].l+tr[rt].r)>>1;
	if(r<=mid) 	return que(ls,l,r);
	else if(l>mid)	return que(rs,l,r);
	else return pushup(que(ls,l,r),que(rs,l,r));//中间情况，查找后合并。
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
		scanf("%d",&a[i]);
	bui(1,1,n);
	int x,y;
	for(int i=1;i<=m;i++)
	{
		scanf("%d%d",&x,&y);
		T tree=que(1,x,y);
		printf("%d %d %d\n",tree.ansl,tree.ansr,tree.ans);
	}
	return 0;
}