树状数组

树状数组

• 区间查询，单点修改(主要求前缀和吧，改一改可以计数)
• 单点查询，区间修改(维护差分数组)
• 区间查询，区间修改(比较麻烦，两个树状数组维护)

区间查询，单点修改(基础）

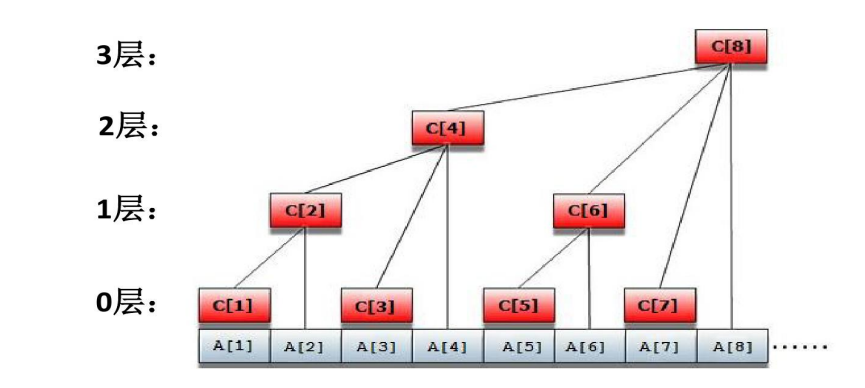
（看图）类似前缀和，(当成前缀和用)，但是为了减少单点修改复杂度写成树状的，每点更新时向上找“根”。
查询时找 \(lowbit\) (二进制中最右边的 \(1\) 和 右边的 \(0\) 组成的数)向叶子找，\(lowbit\)见二进制

void add(int x,int y)
{
	for(;x<=n;x+= (x&-x)) c[x]+=y;
}
int ask(int x)
{
	int ans=0;
	for(;x;x-=(x&-x)) ans+=c[x];
	return ans;
}
int main()
{
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&a[i]);
		add(i,a[i]);
	}
	int x,y;
	scanf("%d%d",&x,&y);
	if()
		add(x,y);
	else
		printf("%d\n",ask(y)-ask(x-1));
	return 0;
}

单点查询，区间修改

正常树状数组只支持区间查询，单点修改，所以想到能不能用前缀和表示一个点的值呢？。。。。差分！差分数组可以查询前缀和查询单点，修改区间第一个元素和区间后的第一个元素就可以实现区间修改（区间修改后内部值相对的变化量不变）。

void add(int x,int y)
{
	for(;x<=n;x+= (x&-x)) c[x]+=y;
}
int ask(int x)
{
	int ans=0;
	for(;x;x-=(x&-x)) ans+=c[x];
	return ans;
}
int main()
{
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&a[i]);
		add(i,a[i]-a[i-1]);
	}
	int x,y,z;
	if()
	{
        scanf("%d%d%d",&x,&y,&z);
		add(x,z); add(y+1,-z);		
	}

	else
	{
		scanf("%d",&x);
		printf("%d\n",ask(x));
	}	
	return 0;
}

区间查询，区间修改

（有点麻烦，能用线段树尽量用线段树）
对于差分数组，区间查询可以解决，但区间修改是个问题，
从差分数组出发，\(a_1+……+a_n\) 等于 \(n*b_1+ (n-1) *b_2+……2 * b_{n-1}+b_n\) ，目标是求后者，即给每一个 \(b_i\) 乘一个系数，因为系数与下标不统一，所以转移一下（见下图）

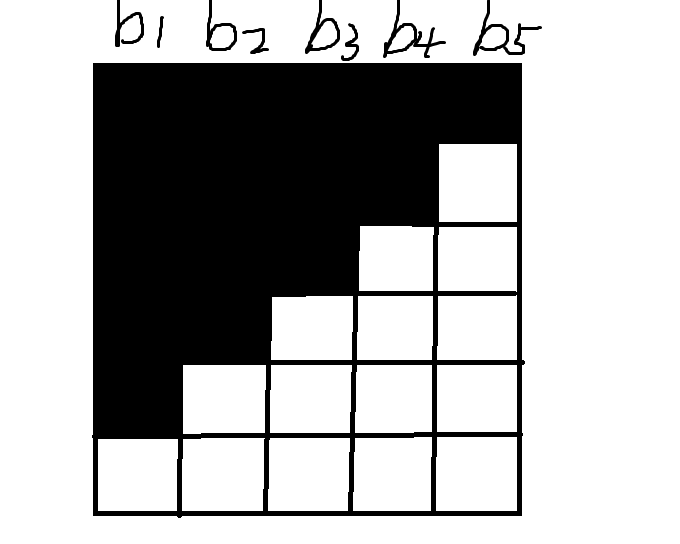
黑色为要求出的部分（\(a_1+……+a_n\)），可由整个矩形 ( $ (n+1) *(a_1+……+a_n) $ ) 减去白色部分（ \(b_1+ 2 *b_2+……(n-1) * b_{n-1}+b_n\) ）,所以可以开两个树状数组，一个存 \(b_n\) 的前缀和，另一个存 \(b_n\) 的“加权”前缀和，最后相减。

code(完整)

#include<iostream>
#include<cstdio>
#include<string>
using namespace std;
long long n,m,a[100005],c[100005],d[100005];
void add(int x,long long y,long long e[])
{
	for(;x<=n;x+=(x&-x)) e[x]+=y;
}
long long ask(int x,long long e[])
{
	long long ans=0;
	for(;x;x-=(x&-x)) ans+=e[x];
	return ans;
}
int main()
{
	scanf("%lld",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%lld",&a[i]);
		add(i,a[i]-a[i-1],c);
		add(i,i*(a[i]-a[i-1]),d);
	}
	scanf("%lld",&m);
	string s;
	int x,y,z;
	for(int i=1;i<=m;i++)
	{
		cin>>s;
		if(s[0]=='S')
		{
			scanf("%d%d",&x,&y);
			long long ans=(ask(y,c)*(y+1)-ask(y,d))-(ask(x-1,c)*x-ask(x-1,d));
			printf("%lld\n",ans);
		}
		else
		{
			scanf("%d%d%d",&x,&y,&z);
			add(x,z,c);
			add(y+1,-z,c);
			add(x,(long long)z*x,d);
			add(y+1,(long long)-z*(y+1),d);
		}
	}
	return 0;
}

感觉树状数组很不方便，很多问题一变形就求不了，不如线段树，但是代码简单。