HH项链(树状数组)

HH项链

题目描述

HH有一串由各种漂亮的贝壳组成的项链。HH相信不同的贝壳会带来好运，所以每次散步完后，他都会随意取出一段贝壳，思考它们所表达的含义。

HH不断地收集新的贝壳，因此他的项链变得越来越长。

有一天，他突然提出了一个问题：某一段贝壳中，包含了多少种不同的贝壳？这个问题很难回答。。。因为项链实在是太长了。

于是，他只好求助睿智的你，来解决这个问题。

输入

第一行：一个整数N，表示项链的长度。

第二行：N个整数，表示依次表示项链中贝壳的编号（编号为0到1000000之间的整数）。

第三行：一个整数M，表示HH询问的个数。

接下来M行：每行两个整数，L和R（1 ≤ L ≤ R ≤ N），表示询问的区间。

N ≤ 50000，M ≤ 200000

输出

M行，每行一个整数，依次表示询问对应的答案。

样例

输入

6
1 2 3 4 3 5
3
1 2 
3 5
2 6

输出

2
2
4

题解

1. 既然要计数，想到用 \(0\) 和 \(1\) 表示选或不选，用树状数组维护前缀和统计个数，由于同种物品有多个，但只计一种，所以每遍历到一个要将上一个同种物品变为 \(0\) ，但如果按询问的顺序查询，无法确定区间内的物品是否被计，可能计到的为 \(0\) ,而 \(1\) 在区间外，错过了。
2. 既然是从左往右遍历，那么每次遇到同种物品都会保留最右侧的，左侧的会变成 \(0\) ，那这样恰好可以用前缀和维护，\(c[r]-c[l-1]\)会将左侧区间外的 \(0\) 舍去，有用的 \(1\) 由于都保存在区间靠右侧了，只要在区间中一定会被计到，但这样要求查询操作的右端点要从小到大，才能实现实时更新前缀和。

3. 离线

既然查询顺序不符合要求，那就让他符合，将所有查询操作记录下来排序后按顺序完成后在按原序输出。

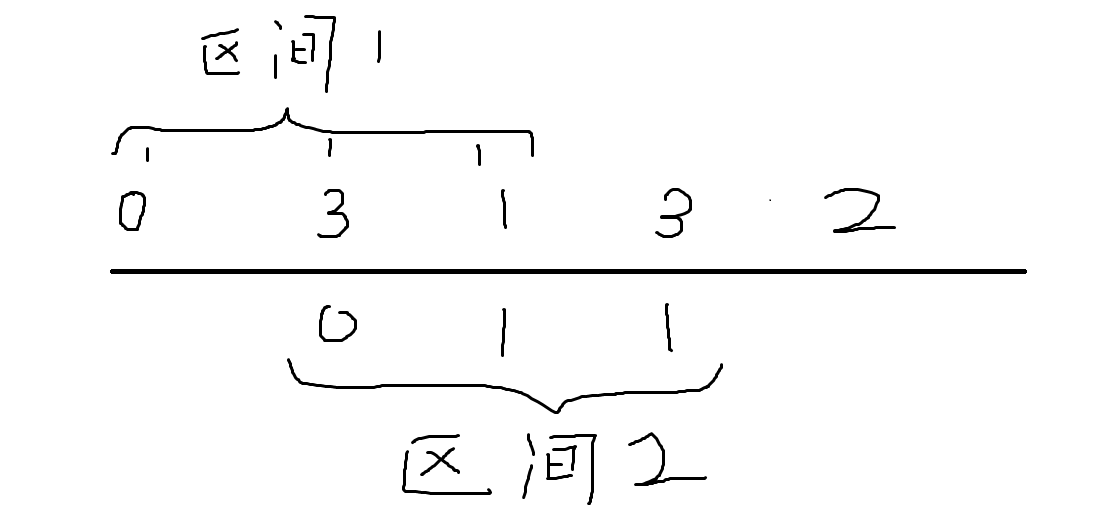
实际效果就像物品遍历赶着区间遍历，每遍历一个或几个物品就向右查询一个区间，将那个标为 \(1\) 的物品始终赶在最前面。

code

int n,a[50005],m,c[50005],ans[200001];
int tem[1000001];

struct A
{
	int l,r,id;
} q[200001];
bool cmp(A x,A y)
{
	return x.r<y.r;
}
int ask(int x)
{
	int ans=0;
	for(;x;x-=(x&-x)) ans+=c[x];
	return ans;
}
void add(int x,int y)
{
	for(;x<=n;x+=(x&-x)) c[x]+=y;
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		scanf("%d",&a[i]);
	scanf("%d",&m);
	for(int i=1;i<=m;i++)
	{
		scanf("%d%d",&q[i].l,&q[i].r);
		q[i].id=i;
	}
	sort(q+1,q+1+m,cmp);
	for(int i=1,j=1;i<=n&&j<=m;i++)
	{
		add(i,1);
		if(tem[a[i]])
		{
			add(tem[a[i]],-1);
		}
		tem[a[i]]=i;
		while(q[j].r==i)
		{
			ans[q[j].id]=ask(q[j].r)-ask(q[j].l-1);
			j++;
		}
	}
	for(int i=1;i<=m;i++) printf("%d\n",ans[i]);
	return 0;	
}