DP
背包
01背包
- 三维基础
\(f[i][j]\)表示前\(i\)个物品放进容量为\(j\)的背包中能获得的最大价值。选物品\(i\)的状态相当于不选\(i\) 的状态\(f[i-1][j-v[i]]\)加上\(i\)的价值\(w[i]\)。
for(int i=1; i<=n; i++)
{
for(int j=1; j<=m; j++)
{
f[i][j] = f[i-1][j];
if(j>=v[i]) f[i][j] = max(f[i][j], f[i-1][j-v[i]] + w[i]);
}
}
- 滚动数组优化
由于转移时只会用到\(i\)和\(i-1\)两行,所以滚一下。
for(int i=1; i<=n; i++)
{
for(int j=1; j<=m; j++)
{
f[i&1][j] = f[(i-1)&1][j];
if(j>=v[i]) f[i&1][j] = max(f[i&1][j], f[(i-1)&1][j-v[i]] + w[i]);
}
}
- 二维
直接将两行合成一行,避免重复选择同一物品,剩余体积\(j\)倒序循环,这时\(f[i][j-v[i]]\)在\(f[i][j]\)的前面,还保留着\(i-1\)这一行的状态,所以和两行的滚动数组一样。
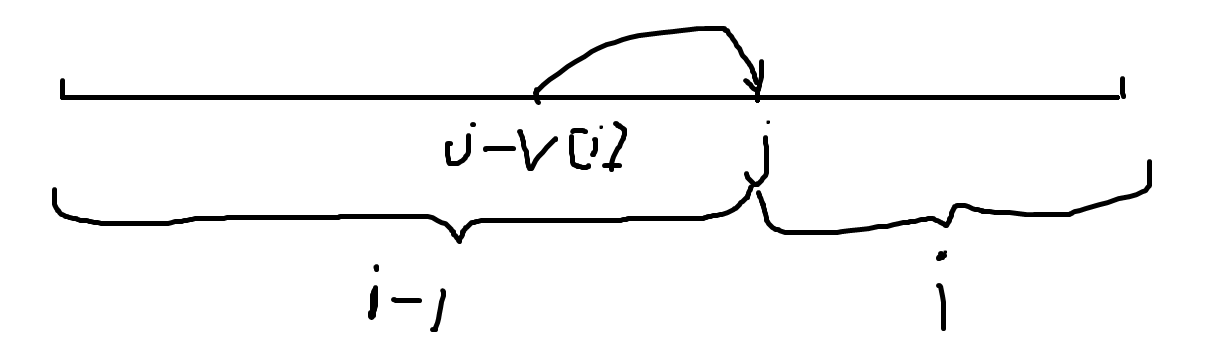
for(int i=1; i<=n; i++)
{
for(int j=m; j>=v[i]; j--)
{
f[j] = max(f[j], f[j-v[i]] + w[i]);
}
}
变形
背包求得是容量为\(m\)的最优值,那如果求第\(k\)优值呢?
Bone Collector II
\(f[j][k]\)表示容量不超过\(j\)的第\(k\)优解,可由\(f[j][1~k]\)和\(f[j-v[i]][1~k]\)转移过来,具体过程类似二分排序,将两组值合并后排序,取第\(k\)优的。
code
for(int i=1;i<=n;i++)
{
for(int j=m;j>=v[i];j--)
{
for(int k=1;k<=K;k++)
{
t1[k]=f[j][k];
t2[k]=f[j-v[i]][k]+w[i];
}
int x=1,y=1,z=1;
while(z<=K&&(x<=K||y<=K))//注意边界
{
if(t1[x]>=t2[y]) f[j][z]=t1[x++];
else f[j][z]=t2[y++];
if(f[j][z]!=f[j][z-1]) z++;//注意有相等的
}
}
}
完全背包
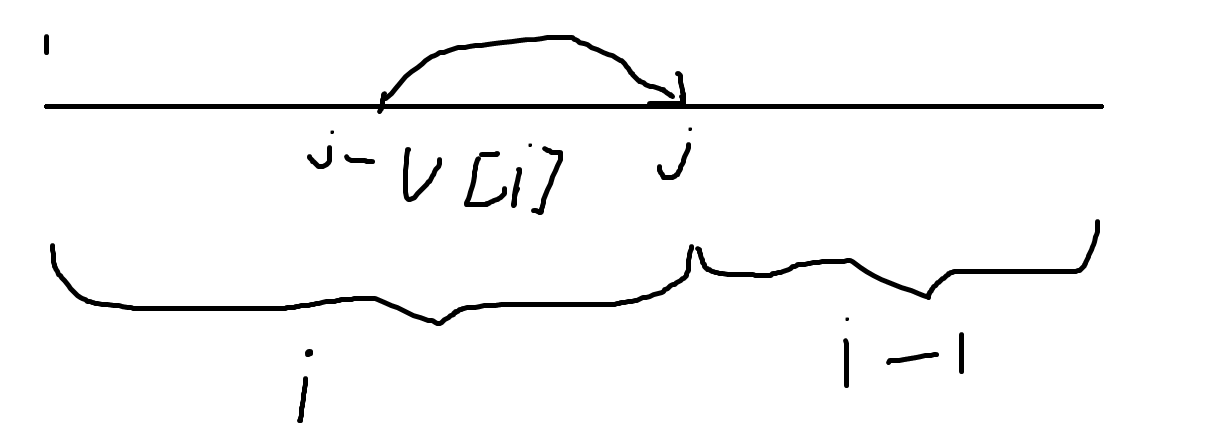
既然01背包倒序循环为了避免重复选同一物品,那同一物品可以选多次的完全背包正序就可以啦!
for(int i=1; i<=n; i++)
{
for(int j=w[i]; j<=m; j++)
{
f[j] = max(f[j], f[j-w[i]] + c[i]);
}
}
多重背包
- 普通版
有几个物品就存几次,跑01背包。
for(int i=1; i<=n; i++)
{
for(int k=1; k<=c[i]; k++)
{
for(int j=m; j>=v[i]; j--)
{
f[j] = max(f[j], f[j-v[i]] + w[i]);
}
}
}
- 二进制拆分
原理:几个 \(2^n\) 相加可以表示任意一个数。
用 \(2^0 \ 2^1… 2^n\) 拆分 \(c[i]\),余下的甩出来单开一个。能保证 \(1 … c[i]\) 一定能用拆分出来的组成。
然后跑01背包。
for(int i=1; i<=n; i++)
{
scanf("%d%d%d", &vi, &wi, &si);
if(si > m / vi) si = m / vi;
for(int j=1; j<=si; j<<=1)
{
v[++cnt] = j * vi;
w[cnt] = j * wi;
si -= j;
}
if(si > 0)
{
v[++cnt] = si * vi;
w[cnt] = si * wi;
}
}
分组背包
和多重背包普通版差不多,由于每一组只能选一个,将组中物品遍历放在背包容量遍历里内,取\(max\)时会自动取最优的。(\(i\)组号,\(j\)容量,\(k\)组内物品)
for(int i=1; i<=t; i++)
{
for(int j=m; j>=0; j--)
{
for(int k=1; k<=g[i][0]; k++)
{
int x = g[i][k];
if(j >= v[x]) f[j] = max(f[j], f[j-v[x]] + w[x]);
}
}
}
变形
分组背包每组最多选一个,如果每组至少选一个呢?
I love sneakers!
\(f[i][j]\) 表示前\(i\)组容量为\(j\)时的最大值,由于每一组可以选多个,组中物品遍历可写在容量遍历外。(参考多重背包)若\(f[i][j-v[x]]\)已经被更新,则第\(i\)组已经选过一个,物品随便选,从本组\(f[i][j-v[x]]\)转移。
若\(f[i-1][j-v[x]]\)被更新,则上一组也可以转移过来,此时物品\(x\)可作为本组第一个,从上一组\(f[i-1][j-v[x]]\)转移。
code
int x,y,z;
memset(g,0,sizeof(g));
for(int i=1;i<=n;i++)
{
scanf("%d%d%d",&x,&y,&z);
g[x][0]++;
g[x][g[x][0]]=i;
v[i]=y; w[i]=z;
}
memset(f,-1,sizeof(f));
f[0][0]=0;
for(int i=1;i<=k;i++)
{
for(int l=1;l<=g[i][0];l++)
{
x=g[i][l];
for(int j=m;j>=v[x];j--)
{
if(f[j-v[x]][i]!=-1)
f[j][i]=max(f[j][i],f[j-v[x]][i]+w[x]);
if(f[j-v[x]][i-1]!=-1)
f[j][i]=max({f[j][i],f[j-v[x]][i-1]+w[x]});
}
}
}
int ans=-1;
for(int i=m;i>0;i--)
{
ans=max(ans,f[i][k]);
}
if(ans==-1) printf("Impossible\n");
else printf("%d\n",ans);
树型背包
题目描述—The more, The Better
ACboy很喜欢玩一种战略游戏,在一个地图上,有N座城堡,每座城堡都有一定的宝物,在每次游戏中ACboy允许攻克M个城堡并获得里面的宝物。但由于地理位置原因,有些城堡不能直接攻克,要攻克这些城堡必须先攻克其他某一个特定的城堡。你能帮ACboy算出要获得尽量多的宝物应该攻克哪M个城堡吗?
输入
3 2
0 1
0 2
0 3
7 4
2 2
0 1
0 4
2 1
7 1
7 6
2 2
0 0
输出
5
13
题解
见树型dp
code
#include<bits/stdc++.h>
using namespace std;
int n,m,f[1005][1005],k[1005];
vector<int> son[1005];
int dfs(int u)
{
int p=1;
f[u][1]=k[u];
for(int v:son[u])
{
int siz=dfs(v);
for(int i=min(m+1,p);i;i--)
for(int j=1;j<=siz&&i+j<=m+1;j++)
f[u][i+j]=max(f[u][i+j],f[u][i]+f[v][j]);
p+=siz;
}
return p;
}
int main()
{
scanf("%d%d",&n,&m);
int x;
for(int i=1;i<=n;i++)
{
scanf("%d%d",&x,&k[i]);
son[x].push_back(i);
}
dfs(0);
printf("%d",f[0][m+1]);
return 0;
}
依赖背包
题目描述—
FJ要去购物,在此之前,他需要一些盒子来装他要买的不同种类的东西。每个盒子都被指定携带一些特定种类的东西(也就是说,如果他要买其中一种东西,他必须事先购买盒子)。每种东西都有自己的价值。现在FJ只有W美元用于购物,他打算用这笔钱获得最高价值。
输入
第一行将包含两个整数,n(框的数量1<=n<=50),w(FJ的金额,1<=w<=100000),然后n行。每行包含以下数字pi(第i个箱子的价格1<=pi<=1000)、mi(第i箱货物可携带的数量1<=mi<=10)和mi对数字,价格cj(1<=cj<=10000),值vj(1</=vj<=100000)
输出
对于每个测试用例,输出FJ可以得到的最大值
输入
3 800
300 2 30 50 25 80
600 1 50 130
400 3 40 70 30 40 35 60
输出
210
先买盒子,在买盒子的基础上跑01背包买物品,类似任意买的分组背包,只不过每一组都要交“过路费”,所以状态转移和分组类似。
for(int i=1;i<=n;i++)
{
scanf("%d%d",&box,&x);
for(int j=box;j<=m;j++)//tem每次都会被覆盖,当成空的就好
tem[j]=f[j-box]+0;// 暂存一下买这个盒子时的状态
for(int j=1;j<=x;j++)
{
scanf("%d%d",&y,&z);
for(int k=m;k>=y+box;k--) //tem只从box开始有意义
tem[k]=max(tem[k],tem[k-y]+z);//转移
}
for(int j=m;j>=0;j--)
f[j]=max(f[j],tem[j]);//从tem复制回来,取最优
}
小优化
普通背包每次都从最大容量\(m\)开始倒叙遍历,大部分更新是无效的,因为它的前一个状态还没有被更新,所以在逐个物品遍历时能不能每输入一个物品就更新一次最大容量,减少无效更新(适用于最大容量不定)
while(scanf("%d",&v))
{
p+=x;
for(int k=p;k>=v;k--)
if(f[k-v])
f[k]=1;
}
背包总结
特点
给定两组(或一组),有一个限制,求这个限制以内的最优解,注意分清价值和限制,有时候其实一样,有时限制和两组值都无关,重点为“限制”和“最优”。
特殊题型
双价值,非负限制
计数(价值为 \(1\))
计数,小优化
方案加计数,互相影响
线性
最长上升子序列
最长上升子序列
线性dp最典型的题,思想很暴力,对于每一个点 \(i\) 从 \(1\) 到 \(i-1\) 遍历一遍,找比自己小的。
\(f[i]\): \(1\) 到 \(i\) 的最长序列,更新\(f[i]=max(f[i],f[j]+1)\)
包括记路径
for(int i=1;i<=n;i++)
{
f[i]=1;
for(int j=1;j<i;j++)
{
if(a[i]>a[j]&&f[i]<f[j]+1)
{
f[i]=f[j]+1;
pre[i]=j;
}
}
if(ans<f[i])
{
ans=f[i];
id=i;
}
}
int cnt=0;
for(int i=id;i;i=pre[i])
{
sun[++cnt]=i;
}
printf("max=%d\n",ans);
for(int i=cnt;i>=1;i--)
{
printf("%d ",a[sun[i]]);
}
线性总结
题型特点,每次更新 \(i\) 都从 \(1\) 到 \(i-1\) 遍历一遍找最优解,序列有一定规律。也会有坐标或图的变形。
(狄尔沃斯定律很好玩)
狄尔沃斯定理:
①对于任意有限偏序集,其最大反链中元素的数目必等于最小链划分中链的数目。
②对于任意有限偏序集,其最长链中元素的数目必等于其最小反链划分中反链的数目
证明一:
对于最长链中的任意一对(两个)元素绝不同时存在于同一反链,或者说划分最小反链中任意一条反链绝不同时包含最长链中的两个元素(因为关系是相反的),因此若最长链中元素个数为n,则最小反链划分最少n条。(鸽巢)
证明二(DJ法):
设有n条最小反链,每条反链都会对最长链最多做出一个贡献,因为:假设存在一条反链没有对最长链做出贡献,说明上一条反链做出的贡献比这条反链上每一个元素能做出的贡献都要大,这时两条反链可以合并为一条反链,与前提存在n条最小反链相矛盾。(通俗一点,假设在反链均为不上升链的情况下,后一条链的最大值一定比前一条链的最小值大,否则两条链可以合并。)所以最长链的元素个数一定为n。
特殊题型
区间
石子合并(1)(2)(3)
(1)
(2)
(3)
思路暴力,遍历每一个区间、每一个区间的合并方式(断点),\(f[i][j]\): \(i\) 到 \(j\) 的最优解,\(f[i][j]=max(f[i][j],f[i][k]+f[k+1][j]+sum[i][j])\) (每次合并都会加一组区间和,所以用前缀和维护一下)。
code
#include<bits/stdc++.h>
using namespace std;
int n,s[105],x,f1[105][105],f2[105][105];
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&x);
s[i]=s[i-1]+x;
}
memset(f1,0x3f,sizeof(f1));
memset(f2,0,sizeof(f2));
for(int i=1;i<=n;i++) f1[i][i]=f2[i][i]=0;
for(int l=1;l<=n;l++)
{
for(int i=1,j=i+l-1;j<=n;i++,j++)
{
for(int k=i;k<j;k++)
{
f1[i][j]=min(f1[i][j],f1[i][k]+f1[k+1][j]+s[j]-s[i-1]);
f2[i][j]=max(f2[i][j],f2[i][k]+f2[k+1][j]+s[j]-s[i-1]);
}
}
}
printf("%d\n",f1[1][n]);
printf("%d",f2[1][n]);
return 0;
}
如果为环形,数组开二倍,模拟环,答案找总长度为 \(2n\) 的数组中找长度为 \(n\) 的一段区间就是环。
code
#include<bits/stdc++.h>
using namespace std;
int n,s[210],a[105],f1[210][210],f2[210][210],ans1=1e9,ans2=0;
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
s[i]=s[i-1]+a[i];
}
for(int i=n+1;i<=n*2;i++) s[i]=s[i-1]+a[i-n];
memset(f1,0x3f,sizeof(f1));
memset(f2,0,sizeof(f2));
for(int i=1;i<=n*2;i++) f1[i][i]=f2[i][i]=0;
for(int l=2;l<=n*2;l++)
{
for(int i=1,j=i+l-1;j<=n*2;i++,j++)
{
for(int k=i;k<j;k++)
{
f1[i][j]=min(f1[i][j],f1[i][k]+f1[k+1][j]+s[j]-s[i-1]);
f2[i][j]=max(f2[i][j],f2[i][k]+f2[k+1][j]+s[j]-s[i-1]);
}
}
}
for(int i=1,j=i+n-1;j<=n*2;i++,j++)
{
ans1=min(f1[i][j],ans1);
ans2=max(f2[i][j],ans2);
}
printf("%d\n%d",ans1,ans2);
return 0;
}
再优化用到一个抽象的定律,即断点 \(k\) 只会在 \(i+1\) 和 \(j-1\) 处最优,因为(下图,没什么用)(如下下图),
不管先合并 \(i p\) 还是 \(p j\), \(f[i][p] , f[p+1][j] , f[i][j] , sum[i][j]\) 都是 一样的,区别只是加 \(sum[i][p]\) 还是 \(sum[p+1][j]\) 的区别,所以为了最大值,让 \(p\) 最靠左或右时最优。

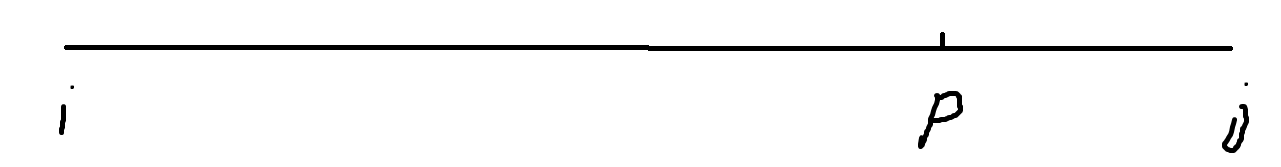
区间总结
题型特点,每次更新以区间为单位,从小区间更新到大区间,如回文,括号,重点放在状态转移方程上。遍历所有区间,所有断点。
特殊题型
坐标
薯塔
数塔
标准走坐标
f[1][1]=a[1][1];
for(int i=2;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
f[i][j]=max(f[i-1][j],f[i-1][j-1])+a[i][j];
}
}
for(int i=1;i<=n;i++) ans=max(ans,f[n][i]);
最大正方形
每一个格子只要右下角三个格子完整就能被更新,注意遍历方向,更新时遵循短板定理,\(f[i][j]\):以\(i ~j\) \(f[i][j]=min({f[i+1][j],f[i][j+1],f[i+1][j+1]})+1\) 。
for(int i=n;i>=1;i--)
{
for(int j=m;j>=1;j--)
{
if(i+1<=n&&j+1<=m)
if((a[i][j])&&(f[i+1][j])&&(f[i][j+1])&&(f[i+1][j+1]))
{
f[i][j]=min({f[i+1][j],f[i][j+1],f[i+1][j+1]})+1;
ans=max(f[i][j],ans);
}
}
}
坐标总结
重点在走坐标的规则,有时候有点像多维的线性dp,序列有规律,\(f[i][j]\) 常表示坐标为 \(i~j\) 处的最优值。
特殊题型
树形
没有上司的舞会
没有上司的舞会
经典树形dp,建树,dfs,用子树更新根。
void dfs(int s)//先找到根,dfs
{
for(int i:son[s])
{
dfs(i);
f[s][0]+=max(f[i][0],f[i][1]);
f[s][1]+=f[i][0];
}
}
树形总结
由于树的分层结构,遍历时使用dfs(或拓扑排序)最合适,从根节点出发,先递归到叶子,更新操作在回溯时完成。
可以参考树形背包。
特殊题型
dp总结
dp就是暴力!!!写法相当暴力,重点在“最优”和“子结构”,抽象成“状态空间”(一维或多维表格),前面背包有点不懂,板子多,写的很详细,后面写的很简略。
发现dp只有两点
- 状态转移方程
- 边界(遍历方式和初始化)
弄清这两点后所有dp都大同小异,区分也不大,只要是求最优解,都可以用暴力方法,如果推不出来就多开一维,再想办法消掉。
遍历时注意无后效性,每一个状态都看成一个阶段,可能被多次更新。


