对比学习入门(1)

对比学习入门

对比学习思想从2018年InstDist^[1]论文中首次提出至今，在2020年左右达到繁盛，如今已经成为了几乎所有深度学习网络训练必备的一环。现如今的计算机视觉，文生图，多模态大模型中都得到了非常广泛地运用。对比学习作为一种无监督学习，不需要人工标签信息并且可以通过一系列数据增强方法扩充数据集，减缓数据稀疏问题。在主任务的基础上使用对比学习优化特征分布可以提升著模型的准确率等指标。

从AutoEncoder开始

AutoEncoder（自动编码器） 是一种神经网络模型，用于数据的降维、特征提取或重建。它是一种无监督学习方法，主要用于学习数据的低维表示或压缩数据，同时尽量保留原始数据的重要特征。如上图所示，我们通过Encoder将Input转换成一个特征向量，这个特征向量保留了Input的信息，再通过Decoder转换成Output。AutoEncoder的训练目标将Output分布尽可能得接近Input分布。

AutoEncoder的设计思想运用在方方面面，卷积神经网络（CNN）、循环神经网络（RNN），图神经网络（GNN） 都有它的身影

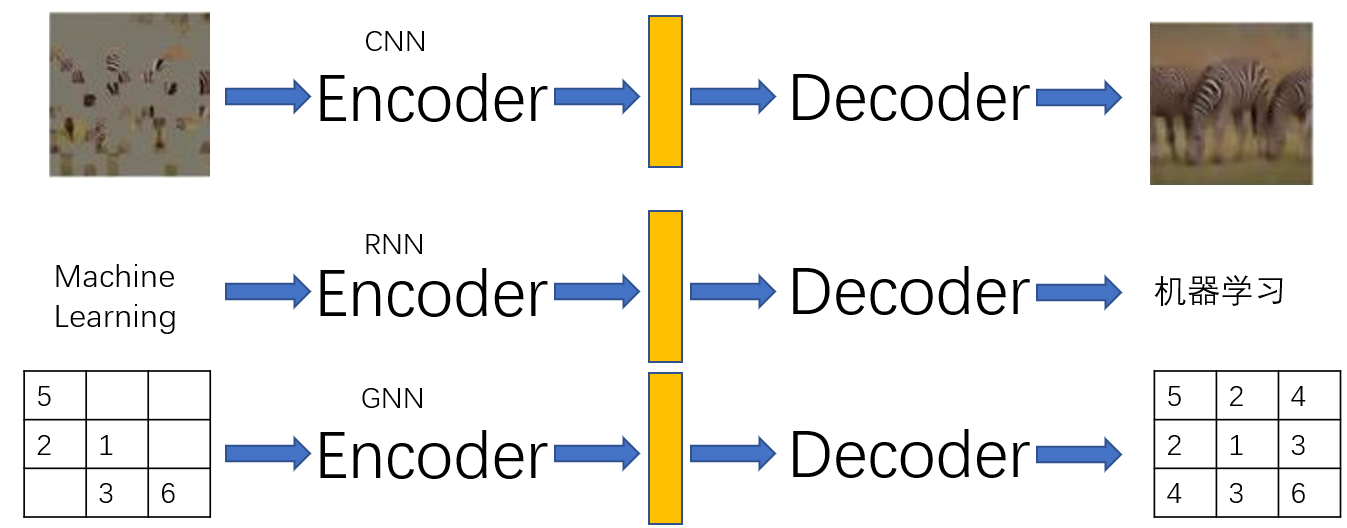
比如在上图的三个例子中，我们将图片作为Input，CNN作为Encoder，我们可以设计一个AutoEncoder用于修复图片。我们可以将"Machine Learning"这句话作为Input，RNN作为Encoder，可以设计一个翻译任务输出"机器学习"。再比如将一个图数据结构的邻接矩阵作为Input，GNN作为Encoder，可以补全邻接矩阵的信息。

进一步来看，无论Input是图片还是文字，都可以通过Encoder编码成一个特征向量，我们通过特征向量配合Decoder可以完成各种事情。如下图所示，我们通过CNN将一张图片编码成特征向量后，可以配合不同Decoder完成物品标识，分类器，图像修复等任务

我们希望能训练出一个最好的特征向量，能包含Input的各种信息，这样就可以在下游Decoder中完成不同的任务。所谓对比学习就是为了训练出一个足够好的特征向量用于下游任务。如下图所示，训练一个足够好的特征就是对比学习的目标

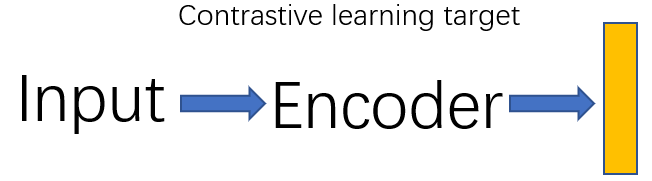
但是“足够好的特征”是一个非常抽象的概念，深度学习中一般使用64维、128维、256维的向量描述Input，但是这个向量中的具体数值我们并不清楚，并且这个数字是不是足够好对我们来说也很抽象。所以这是一个无监督训练，因为我们并没有一个具体标签或者具体数字用于训练。为了训练出”足够好的特征”，我们需要对“足够好”这件事情进行定义。

定义一个足够好的特征

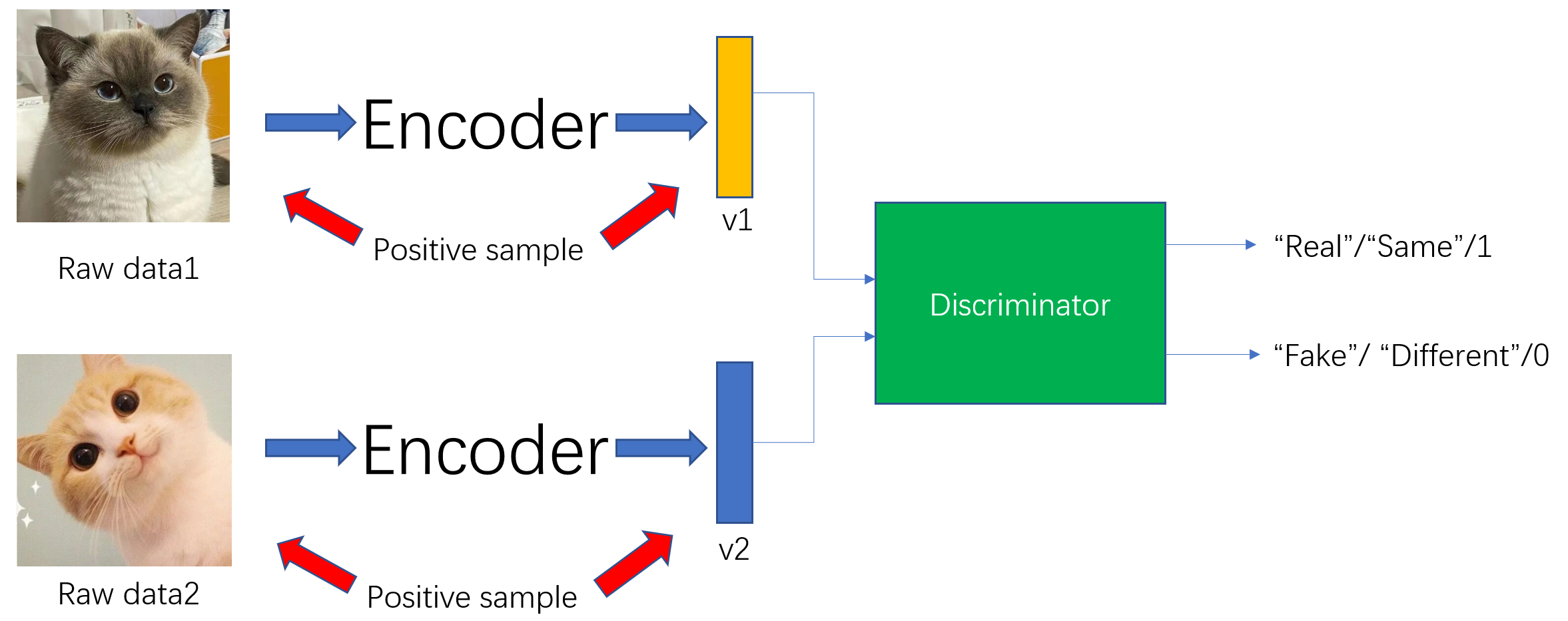
我们还是以一个例子来说明，什么样的特征足够好。比如我们有两张猫咪的图片raw data1和raw data2，如下图所示，他们通过同一个Encoder得到了各自的特征向量v1和v2。

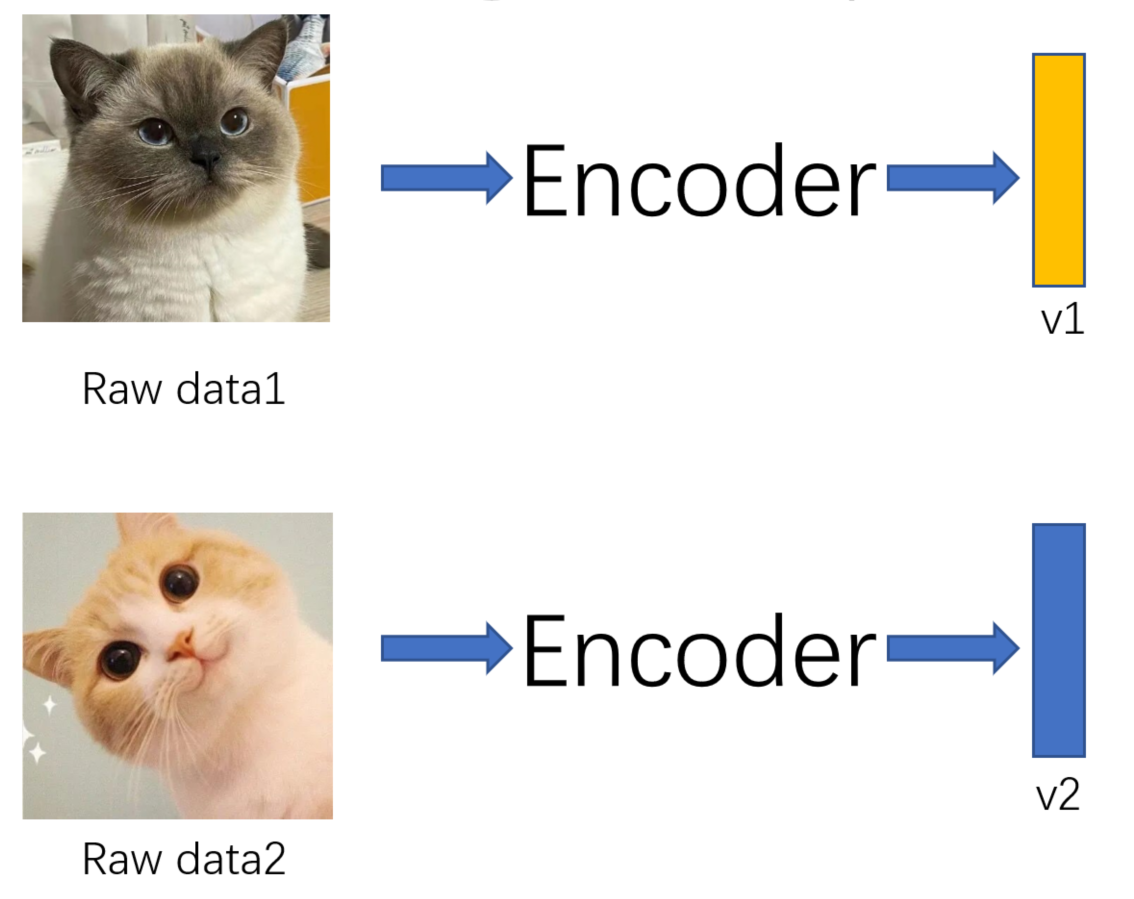
我们可以训练一个Discriminator辨别器，用于判断Input数据是不是和特征向量一一对应，如下图所示。比如，我们将data1和v1输入到辨别器中，它发现两者一一对应，输出“Real”。我们将data1和v2输入到辨别器中，它发现两者并不是一一对应关系，输出“Fake"。通过这个辨别器一直训练下去，data1和v1的相似度就会越来越高，data1和v2的相似度越来越低。换句话说就是v1特征真的能代表data1这个数据，那它就是一个我们认为足够好的特征了。

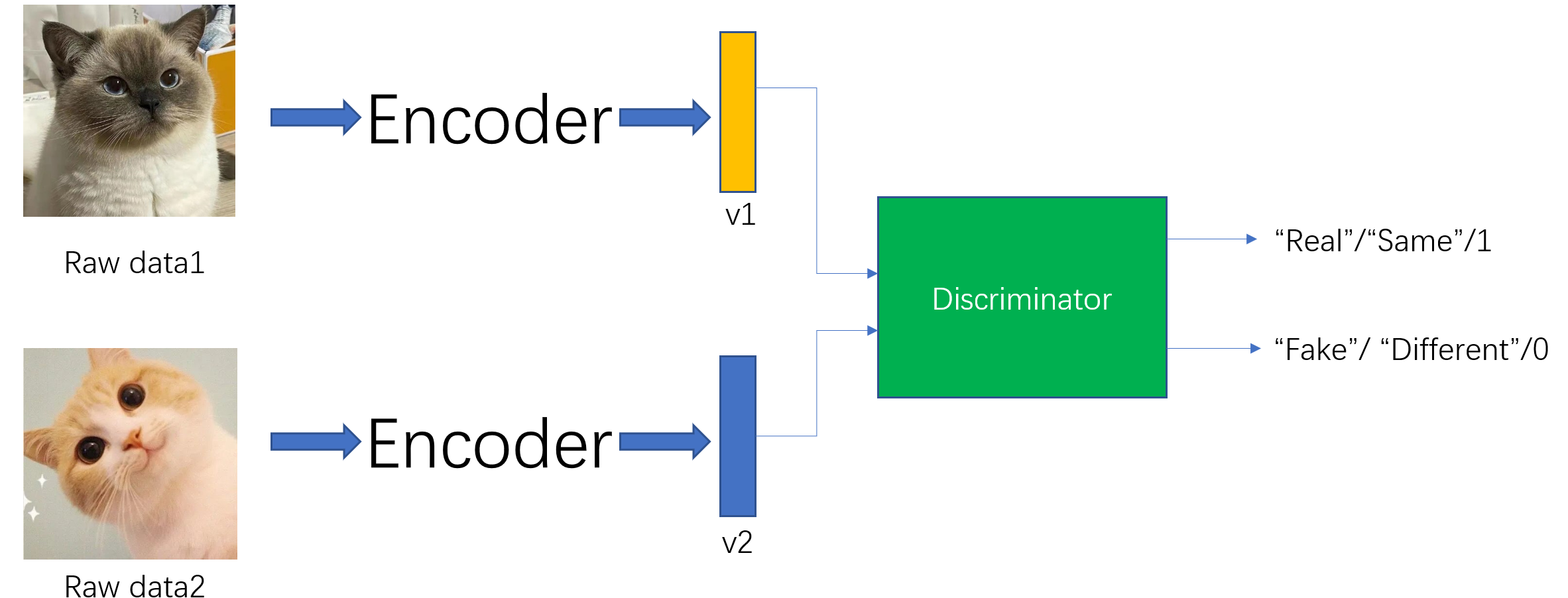
如下图所示，在这个例子中，判别器的正样本的是正确的一一对应关系，而负样本就是错误的对应关系

对比学习的开山论文InstDisc^[1:1]

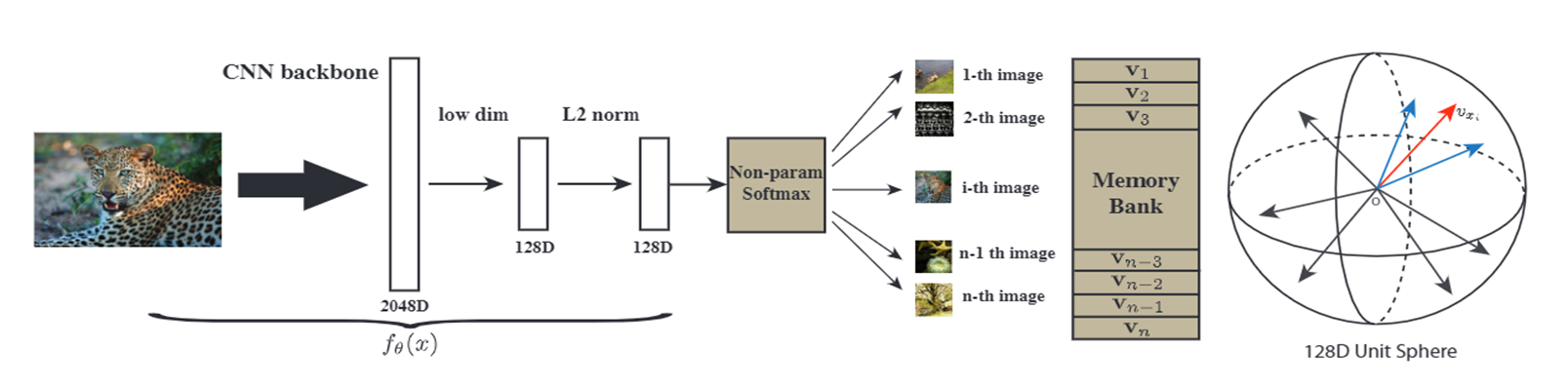
论文全名《Unsupervised Feature Learning via non-Parametric Instance Discrimination》将图像分类任务看作是一个个体判别任务，也就是我们上一节讲的一一对应关系。在上图中，它将一张图片通过CNN编码器降维成一个128维度的特征向量，将这些特征向量送到一个判别器中进行训练，最后的特征分布就像最右边的球展示的，每个特征保证自己和其他特征分离。

论文中作者遇到一个问题，由于将每张图片都最为一个单独的类别，导致softmax函数的复杂度太大了，所以作者使用NCE Loss进行近似计算。这一步用现在的眼光来看简直就是一个里程碑的思想。它不再通过网络权重计算softmax，而是修改成特征向量v，在$||v||=1$的 同时引入温度超参数$\tau$用来控制分布的concentration level。公式如下

$$\begin{array}{}\text{(Eq.1)}& P(i|v)=\frac{exp(v_i^{T}v/\tau )}{\sum _{j=1}^{n}exp(v_j^{T}v/\tau )}.\end{array}$$

这短短一句话中的三个改进都是对比学习中至关重要的改进点。NCE Loss将softmax看作是一个正负样本二分类问题进行简化。假设负样本为噪声，分布为$P_n=1/n$为均匀分布,并且假设噪声分布是正样本分布的m倍，那么正样本（D=1）的概率计算公式如下:

$$\begin{array}{}\text{(Eq.2)}& P(D=1|i,v)=\frac{P(i|v)}{P(i|v)+m{P}_n(i)},\end{array}$$

所以Loss function的最小化公式如下，经验风险最小化在建模条件概率分布以及损失函数为对数情况下等价于极大似然估计。这个期望其实就是经验风险中样本数量趋于无穷大时等价于期望风险。

$$\begin{array}{}\text{(Eq.3)}& J_{NCE}(\theta )=-E_{P_d}[\log h(i,v)]-m\cdot E_{P_n}[\log (1-h(i,v^{\prime }))],\end{array}$$

由于每一个个体在一轮epoch训练中只会被使用一次，所以学习梯度会非常陡峭，由此引入L2正则化让学习曲线更加光滑，其中$v_i^{(t)}=f_{\theta }(x_i)$为当前epoch的特征, 而memory bank中存有之前的$v^{(t-1)}$ ，公式如下

$$\begin{array}{}\text{(Eq.4)}& \lambda ||v_i^{(t)}-v_i^{(t-1)}|{|}_2^2\end{array}$$

最终Loss function如下:

$$\begin{array}{}\text{(Eq.5)}& J_{NCE}(\theta )=-E_{P_d}[\log h(i,v)-\lambda ||v_i^{(t)}-v_i^{(t-1)}|{|}_2^2]-m\cdot E_{P_n}[\log (1-h(i,v^{\prime }))].\end{array}$$

当负样本数量趋于无穷时, NCE目标函数的梯度和MLE对数似然函数梯度是等价的, 也就是说我们通过NCE转换后的优化目标, 本质上就是对极大似然估计方法的一种近似, 并且随着负样本和正样本数量比的增大, 这种近似越精确, 这也解释了为什么作者建议我们将设置的越大越好。

---

1. Wu Z, Xiong Y, Yu S X, et al. Unsupervised feature learning via non-parametric instance discrimination[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2018: 3733-3742. ↩︎ ↩︎