加解密篇 - 非对称加密算法 (RSA、DSA、ECC、DH)

最近的文章中多次出现了非对称加密，今天就来分析一下非对称加密的算法。

简介
RSA算法
DSA算法
ECC算法
DH算法

1. 简介

1.1 概念

非对称加密需要两个密钥：公钥 (publickey) 和私钥 (privatekey)。公钥和私钥是一对，如果用公钥对数据加密，那么只能用对应的私钥解密。如果用私钥对数据加密，只能用对应的公钥进行解密。因为加密和解密用的是不同的密钥，所以称为非对称加密。

非对称加密算法的保密性好，它消除了最终用户交换密钥的需要。但是加解密速度要远远慢于对称加密，在某些极端情况下，甚至能比对称加密慢上1000倍。

1.2 特点

算法强度复杂、安全性依赖于算法与密钥但是由于其算法复杂，而使得加密解密速度没有对称加密解密的速度快。对称密码体制中只有一种密钥，并且是非公开的，如果要解密就得让对方知道密钥。所以保证其安全性就是保证密钥的安全，而非对称密钥体制有两种密钥，其中一个是公开的，这样就可以不需要像对称密码那样传输对方的密钥了。这样安全性就大了很多。

1.3 工作原理

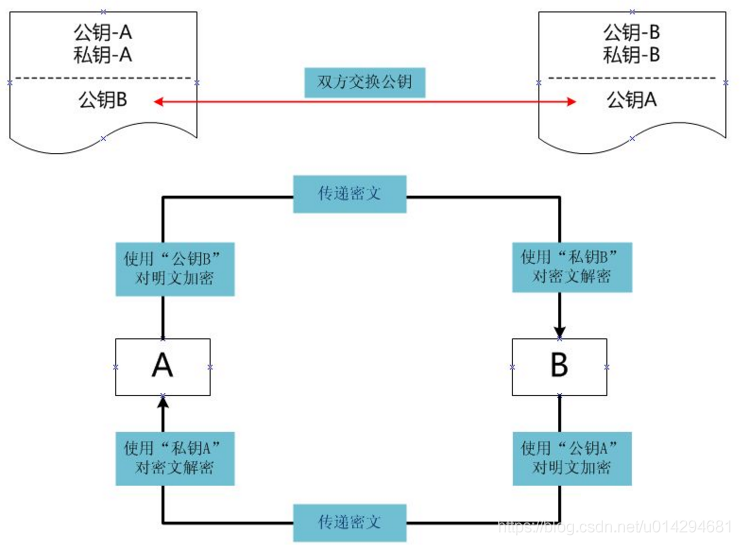
(1) A 要向 B 发送信息，A 和 B 都要产生一对用于加密和解密的公钥和私钥。
(2) A 的私钥保密，A 的公钥告诉 B；B 的私钥保密，B 的公钥告诉 A。
(3) A 要给 B 发送信息时，A 用 B 的公钥加密信息，因为 A 知道 B 的公钥。
(4) A 将这个消息发给 B (已经用 B 的公钥加密消息)。
(5) B 收到这个消息后，B 用自己的私钥解密 A 的消息。其他所有收到这个报文的人都无法解密，因为只有 B 才有 B 的私钥。

1.4 主要算法

RSA、Elgamal、背包算法、Rabin、D-H、ECC (椭圆曲线加密算法)。使用最广泛的是 RSA 算法，Elgamal 是另一种常用的非对称加密算法。

1.5 应用场景

(1) 信息加密

收信者是唯一能够解开加密信息的人，因此收信者手里的必须是私钥。发信者手里的是公钥，其它人知道公钥没有关系，因为其它人发来的信息对收信者没有意义。

(2) 登录认证

客户端需要将认证标识传送给服务器，此认证标识 (可能是一个随机数) 其它客户端可以知道，因此需要用私钥加密，客户端保存的是私钥。服务器端保存的是公钥，其它服务器知道公钥没有关系，因为客户端不需要登录其它服务器。

(3) 数字签名

数字签名是为了表明信息没有受到伪造，确实是信息拥有者发出来的，附在信息原文的后面。就像手写的签名一样，具有不可抵赖性和简洁性。

简洁性：对信息原文做哈希运算，得到消息摘要，信息越短加密的耗时越少。

不可抵赖性：信息拥有者要保证签名的唯一性，必须是唯一能够加密消息摘要的人，因此必须用私钥加密 (就像字迹他人无法学会一样)，得到签名。如果用公钥，那每个人都可以伪造签名了。

(4) 数字证书

问题起源：对1和3，发信者怎么知道从网上获取的公钥就是真的？没有遭受中间人攻击？

这样就需要第三方机构来保证公钥的合法性，这个第三方机构就是 CA (Certificate Authority)，证书中心。

CA 用自己的私钥对信息原文所有者发布的公钥和相关信息进行加密，得出的内容就是数字证书。

信息原文的所有者以后发布信息时，除了带上自己的签名，还带上数字证书，就可以保证信息不被篡改了。信息的接收者先用 CA给的公钥解出信息所有者的公钥，这样可以保证信息所有者的公钥是真正的公钥，然后就能通过该公钥证明数字签名是否真实了。

这个的实际应用可以看看我之前的文章：网络篇 - https协议中的数据是否需要二次加密，里面讲的比较详细。

2. RSA算法

2.1 简介

RSA 是目前最有影响力的公钥加密算法，该算法基于一个十分简单的数论事实：将两个大素数相乘十分容易，但想要对其乘积进行因式分解却极其困难，因此可以将乘积公开作为加密密钥，即公钥，而两个大素数组合成私钥。公钥是可发布的供任何人使用，私钥则为自己所有，供解密之用。

2.2 工作流程

A 要把信息发给 B 为例，确定角色：A 为加密者，B 为解密者。首先由 B 随机确定一个 KEY，称之为私钥，将这个 KEY 始终保存在机器 B 中而不发出来；然后，由这个 KEY 计算出另一个 KEY，称之为公钥。这个公钥的特性是几乎不可能通过它自身计算出生成它的私钥。接下来通过网络把这个公钥传给 A，A 收到公钥后，利用公钥对信息加密，并把密文通过网络发送到 B，最后 B 利用已知的私钥，就能对密文进行解码了。以上就是 RSA 算法的工作流程。

2.3 运算速度

由于进行的都是大数计算，使得 RSA 最快的情况也比 DES 慢上好几倍，无论是软件还是硬件实现。速度一直是 RSA 的缺陷。一般来说只用于少量数据加密。RSA 的速度是对应同样安全级别的对称密码算法的1/1000左右。

比起 DES 和其它对称算法来说，RSA 要慢得多。实际上一般使用一种对称算法来加密信息，然后用 RSA 来加密比较短的公钥，然后将用 RSA 加密的公钥和用对称算法加密的消息发送给接收方。

这样一来对随机数的要求就更高了，尤其对产生对称密码的要求非常高，否则的话可以越过 RSA 来直接攻击对称密码。

2.4 公钥传递安全

和其它加密过程一样，对 RSA 来说分配公钥的过程是非常重要的。分配公钥的过程必须能够抵挡中间人攻击。假设 A 交给 B 一个公钥，并使 B 相信这是A 的公钥，并且 C 可以截下 A 和 B 之间的信息传递，那么 C 可以将自己的公钥传给 B，B 以为这是 A 的公钥。C 可以将所有 B 传递给 A 的消息截下来，将这个消息用自己的密钥解密，读这个消息，然后将这个消息再用 A 的公钥加密后传给 A。理论上 A 和 B 都不会发现 C 在偷听它们的消息，今天人们一般用数字认证来防止这样的攻击。

2.5 攻击

(1) 针对 RSA 最流行的攻击一般是基于大数因数分解。1999年，RSA-155 (512 bits) 被成功分解，花了五个月时间（约8000 MIPS 年）和224 CPU hours 在一台有3.2G 中央内存的 Cray C916计算机上完成。

RSA-158 表示如下：

39505874583265144526419767800614481996020776460304936454139376051579355626529450683609727842468219535093544305870490251995655335710209799226484977949442955603= 3388495837466721394368393204672181522815830368604993048084925840555281177× 11658823406671259903148376558383270818131012258146392600439520994131344334162924536139

2009年12月12日，编号为 RSA-768 (768 bits, 232 digits) 数也被成功分解。这一事件威胁了现通行的1024-bit 密钥的安全性，普遍认为用户应尽快升级到2048-bit 或以上。

RSA-768表示如下：

1230186684530117755130494958384962720772853569595334792197322452151726400507263657518745202199786469389956474942774063845925192557326303453731548268507917026122142913461670429214311602221240479274737794080665351419597459856902143413= 3347807169895689878604416984821269081770479498371376856891 2431388982883793878002287614711652531743087737814467999489× 3674604366679959042824463379962795263227915816434308764267 6032283815739666511279233373417143396810270092798736308917

(2) 秀尔算法

量子计算里的秀尔算法能使穷举的效率大大的提高。由于 RSA 算法是基于大数分解 (无法抵抗穷举攻击)，因此在未来量子计算能对 RSA 算法构成较大的威胁。一个拥有 N 量子位的量子计算机，每次可进行2^N 次运算，理论上讲，密钥为1024位长的 RSA 算法，用一台512量子比特位的量子计算机在1秒内即可破解。

2.6 例子

private static final String ALGO = "RSA";
private static final String CHARSET = "UTF-8";
/*
* 用于存储随机产生的公钥与私钥
*/
private static Map<Integer, String> KEY_CACHE = new HashMap<>();
/**
* 随机生成密钥对
*
* @throws NoSuchAlgorithmException
*/
private static void generateKeyPair() throws NoSuchAlgorithmException {
// KeyPairGenerator 类用于生成公钥和私钥对，基于RSA算法生成对象
KeyPairGenerator keyPairGen = KeyPairGenerator.getInstance(ALGO);
// 初始化密钥对生成器，密钥大小为 96-1024 位
keyPairGen.initialize(1024, new SecureRandom());
// 生成一个密钥对，保存在 keyPair 中
KeyPair keyPair = keyPairGen.generateKeyPair();
// 得到私钥
RSAPrivateKey privateKey = (RSAPrivateKey) keyPair.getPrivate();
// 得到公钥
RSAPublicKey publicKey = (RSAPublicKey) keyPair.getPublic();
String publicKeyString = new String(Base64.getEncoder().encode(publicKey.getEncoded()));
// 得到私钥字符串
String privateKeyString = new String(Base64.getEncoder().encode((privateKey.getEncoded())));
// 将公钥和私钥保存到 Map
KEY_CACHE.put(0, publicKeyString);
KEY_CACHE.put(1, privateKeyString);
}
/**
* RSA公钥加密
*
* @param data 加密字符串
* @param publicKey 公钥
* @return 密文
* @throws Exception 加密过程中的异常信息
*/
private static String encrypt(String data, String publicKey) throws Exception {
// base64 编码的公钥
byte[] decoded = Base64.getDecoder().decode(publicKey);
RSAPublicKey pubKey = (RSAPublicKey) KeyFactory.getInstance(ALGO).generatePublic(new X509EncodedKeySpec(decoded));
// RSA加密
Cipher cipher = Cipher.getInstance(ALGO);
// 公钥加密
cipher.init(Cipher.ENCRYPT_MODE, pubKey);
return Base64.getEncoder().encodeToString(cipher.doFinal(data.getBytes(CHARSET)));
}
/**
* RSA私钥解密
*
* @param data 加密字符串
* @param privateKey 私钥
* @return 铭文
* @throws Exception 解密过程中的异常信息
*/
private static String decrypt(String data, String privateKey) throws Exception {
byte[] inputByte = Base64.getDecoder().decode(data.getBytes(CHARSET));
// base64 编码的私钥
byte[] decoded = Base64.getDecoder().decode(privateKey);
RSAPrivateKey priKey = (RSAPrivateKey) KeyFactory.getInstance(ALGO).generatePrivate(new PKCS8EncodedKeySpec(decoded));
// RSA 解密
Cipher cipher = Cipher.getInstance(ALGO);
// 私钥解密
cipher.init(Cipher.DECRYPT_MODE, priKey);
return new String(cipher.doFinal(inputByte));
}
public static void main(String[] args) {
String originData = "hellp Test Asymmetric encrypt!";
try {
generateKeyPair();
String encryData = encrypt(originData, KEY_CACHE.get(0));
System.out.println("encryData = " + encryData);
String decryData = decrypt(encryData, KEY_CACHE.get(1));
System.out.println("decryData = " + decryData);
} catch (Exception e) {
e.printStackTrace();
}
}

执行输出：

encryData = Agp72Awcbwy9/8qCFN7VBEwek9LRhjdOqT6JA3MaLOIrEc/VR85vW/q/dL4WOl6ELlyd0L4dieikfw0U94FuH+lyTItEen33lzRszW+xjH8ElSH1/W/3SoAm0r7qRdJ+GoHpRXNGwsnoS77mhYtn743txX1O4bjIdZrLwQZB/6I=
decryData = hellp Test Asymmetric encrypt!

3. DSA算法

3.1 简介

DSA (Digital Signature Algorithm) 是 Schnorr 和 ElGamal 签名算法的变种，被美国 NIST 作为 DSS (DigitalSignature Standard)。 DSA 是基于整数有限域离散对数难题的。

简单的说，这是一种更高级的验证方式，用作数字签名。不单单只有公钥、私钥，还有数字签名。私钥加密生成数字签名，公钥验证数据及签名，如果数据和签名不匹配则认为验证失败。数字签名的作用就是校验数据在传输过程中不被修改，数字签名，是单向加密的升级。

3.2 处理过程

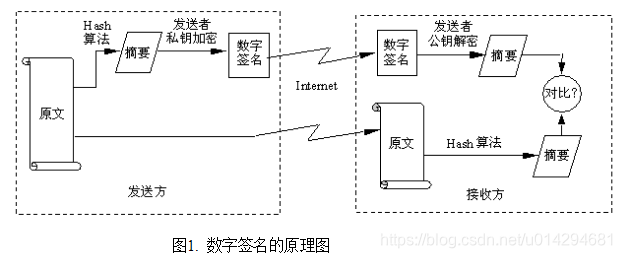
(1) 使用消息摘要算法将发送数据加密生成数字摘要。
(2) 发送方用自己的私钥对摘要再加密，形成数字签名。
(3) 将原文和加密的摘要同时传给对方。
(4) 接受方用发送方的公钥对摘要解密，同时对收到的数据用消息摘要算法产生同一摘要。
(5) 将解密后的摘要和收到的数据在接收方重新加密产生的摘要相互对比，如果两者一致，则说明在传送过程中信息没有破坏和篡改。否则，则说明信息已经失去安全性和保密性。

具体可以看这篇：网络篇 - https协议中的数据是否需要二次加密

3.3 例子

/**
* DSA安全编码组件
*/
public abstract class DSACoder extends Coder {
public static final String ALGORITHM = "DSA";
/**
* 默认密钥字节数
*
* <pre>
* DSA
* Default Keysize 1024
* Keysize must be a multiple of 64, ranging from 512 to 1024 (inclusive).
* </pre>
*/
private static final int KEY_SIZE = 1024;
/**
* 默认种子
*/
private static final String DEFAULT_SEED = "0f22507a10bbddd07d8a3082122966e3";
private static final String PUBLIC_KEY = "DSAPublicKey";
private static final String PRIVATE_KEY = "DSAPrivateKey";
/**
* 用私钥对信息生成数字签名
*
* @param data
* 加密数据
* @param privateKey
* 私钥
*
* @return
* @throws Exception
*/
public static String sign(byte[] data, String privateKey) throws Exception {
// 解密由base64编码的私钥
byte[] keyBytes = decryptBASE64(privateKey);
// 构造PKCS8EncodedKeySpec对象
PKCS8EncodedKeySpec pkcs8KeySpec = new PKCS8EncodedKeySpec(keyBytes);
// KEY_ALGORITHM 指定的加密算法
KeyFactory keyFactory = KeyFactory.getInstance(ALGORITHM);
// 取私钥匙对象
PrivateKey priKey = keyFactory.generatePrivate(pkcs8KeySpec);
// 用私钥对信息生成数字签名
Signature signature = Signature.getInstance(keyFactory.getAlgorithm());
signature.initSign(priKey);
signature.update(data);
return encryptBASE64(signature.sign());
}
/**
* 校验数字签名
*
* @param data
* 加密数据
* @param publicKey
* 公钥
* @param sign
* 数字签名
*
* @return 校验成功返回true 失败返回false
* @throws Exception
*
*/
public static boolean verify(byte[] data, String publicKey, String sign)
throws Exception {
// 解密由base64编码的公钥
byte[] keyBytes = decryptBASE64(publicKey);
// 构造X509EncodedKeySpec对象
X509EncodedKeySpec keySpec = new X509EncodedKeySpec(keyBytes);
// ALGORITHM 指定的加密算法
KeyFactory keyFactory = KeyFactory.getInstance(ALGORITHM);
// 取公钥匙对象
PublicKey pubKey = keyFactory.generatePublic(keySpec);
Signature signature = Signature.getInstance(keyFactory.getAlgorithm());
signature.initVerify(pubKey);
signature.update(data);
// 验证签名是否正常
return signature.verify(decryptBASE64(sign));
}
/**
* 生成密钥
*
* @param seed
* 种子
* @return 密钥对象
* @throws Exception
*/
public static Map<String, Object> initKey(String seed) throws Exception {
KeyPairGenerator keygen = KeyPairGenerator.getInstance(ALGORITHM);
// 初始化随机产生器
SecureRandom secureRandom = new SecureRandom();
secureRandom.setSeed(seed.getBytes());
keygen.initialize(KEY_SIZE, secureRandom);
KeyPair keys = keygen.genKeyPair();
DSAPublicKey publicKey = (DSAPublicKey) keys.getPublic();
DSAPrivateKey privateKey = (DSAPrivateKey) keys.getPrivate();
Map<String, Object> map = new HashMap<String, Object>(2);
map.put(PUBLIC_KEY, publicKey);
map.put(PRIVATE_KEY, privateKey);
return map;
}
/**
* 默认生成密钥
*
* @return 密钥对象
* @throws Exception
*/
public static Map<String, Object> initKey() throws Exception {
return initKey(DEFAULT_SEED);
}
/**
* 取得私钥
*
* @param keyMap
* @return
* @throws Exception
*/
public static String getPrivateKey(Map<String, Object> keyMap)
throws Exception {
Key key = (Key) keyMap.get(PRIVATE_KEY);
return encryptBASE64(key.getEncoded());
}
/**
* 取得公钥
*
* @param keyMap
* @return
* @throws Exception
*/
public static String getPublicKey(Map<String, Object> keyMap)
throws Exception {
Key key = (Key) keyMap.get(PUBLIC_KEY);
return encryptBASE64(key.getEncoded());
}
}

4. ECC算法

4.1 简介

椭圆加密算法（ECC）是一种公钥加密算法，最初由 Koblitz 和 Miller 两人于1985年提出，其数学基础是利用椭圆曲线上的有理点构成 Abel 加法群上椭圆离散对数的计算困难性。公钥密码体制根据其所依据的难题一般分为三类：大整数分解问题类、离散对数问题类、椭圆曲线类。有时也把椭圆曲线类归为离散对数类。

ECC 的主要优势是在某些情况下它比其他的方法使用更小的密钥 (比如 RSA)，提供相当的或更高等级的安全。ECC 的另一个优势是可以定义群之间的双线性映射，基于 Weil 对或是 Tate 对；双线性映射已经在密码学中发现了大量的应用，例如基于身份的加密。不过一个缺点是加密和解密操作的实现比其他机制花费的时间长。

ECC 被广泛认为是在给定密钥长度的情况下，最强大的非对称算法，因此在对带宽要求十分紧的连接中会十分有用。

比特币钱包公钥的生成使用了椭圆曲线算法，通过椭圆曲线乘法可以从私钥计算得到公钥，这是不可逆转的过程。

4.2 优势

(1) 安全性高，有研究表示160位的椭圆密钥与1024位的 RSA 密钥安全性相同。

(2) 处理速度快，在私钥的加密解密速度上，ECC 算法比 RSA、DSA 速度更快，存储空间占用小，带宽要求低。

4.3 例子

https://github.com/esxgx/easy-ecc

Java 中 Chipher、Signature、KeyPairGenerator、KeyAgreement、SecretKey 均不支持 ECC 算法。

5. DH算法

5.1 简介

DH，全称为"Diffie-Hellman"，它是一种确保共享 KEY 安全穿越不安全网络的方法，也就是常说的密钥一致协议。由公开密钥密码体制的奠基人 Diffie 和 Hellman 所提出的一种思想。简单的说就是允许两名用户在公开媒体上交换信息以生成"一致"的、可以共享的密钥。也就是由甲方产出一对密钥 (公钥、私钥)，乙方依照甲方公钥产生乙方密钥对 (公钥、私钥)。

以此为基线，作为数据传输保密基础，同时双方使用同一种对称加密算法构建本地密钥 (SecretKey) 对数据加密。这样，在互通了本地密钥 (SecretKey) 算法后，甲乙双方公开自己的公钥，使用对方的公钥和刚才产生的私钥加密数据，同时可以使用对方的公钥和自己的私钥对数据解密。不单单是甲乙双方两方，可以扩展为多方共享数据通讯，这样就完成了网络交互数据的安全通讯。

5.2 例子

具体例子可以移步到这篇文章：非对称密码之DH密钥交换算法

posted @ 2022-01-11 16:15 门罗的魔术师阅读(2350) 评论(0) 编辑收藏举报

刷新页面返回顶部

魔术师

加解密篇 - 非对称加密算法 (RSA、DSA、ECC、DH)

公告