算法解析：LeetCode——机器人碰撞和最低票价
摘要：本文由葡萄城技术团队原创。转载请注明出处：葡萄城官网，葡萄城为开发者提供专业的开发工具、解决方案和服务，赋能开发者。
机器人碰撞
问题：
现有 n 个机器人，编号从 1 开始，每个机器人包含在路线上的位置、健康度和移动方向。 给你下标从 0 开始的两个整数数组 positions、healths 和一个字符串 directions（directions[i] 为 'L' 表示 向左 或 'R' 表示 向右）。positions 中的所有整数 互不相同 。 所有机器人以相同速度同时沿给定方向在路线上移动。如果两个机器人移动到相同位置，则会发生 碰撞 。 如果两个机器人发生碰撞，则将 健康度较低 的机器人从路线中 移除 ，并且另一个机器人的健康度 减少 1 。 幸存下来的机器人将会继续沿着与之前 相同 的方向前进。如果两个机器人的健康度相同，则将二者都从路线中移除。 请你确定全部碰撞后幸存下的所有机器人的 健康度 ，并按照原来机器人编号的顺序排列。 即机器人 1 （如果幸存）的最终健康度，机器人 2 （如果幸存）的最终健康度等。 如果不存在幸存的机器人，则返回空数组。 在不再发生任何碰撞后，请你以数组形式，返回所有剩余机器人的健康度（按机器人输入中的编号顺序）。
示例 ：
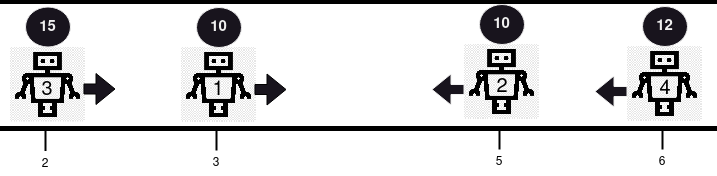
输入：positions = [3,5,2,6], healths = [10,10,15,12], directions = "RLRL" 输出：[14] 解释：本例中发生 2 次碰撞。首先，机器人 1 和机器人 2 将会碰撞，因为二者健康度相同，二者都将被从路线中移除。接下来，机器人 3 和机器人 4 将会发生碰撞，由于机器人 4 的健康度更小，则它会被移除，而机器人 3 的健康度变为 15 - 1 = 14 。仅剩机器人 3 ，所以返回 [14] 。
提示： 1 <= positions.length == healths.length == directions.length == n <= 105 1 <= positions[i], healths[i] <= 109 directions[i] == 'L' 或 directions[i] == 'R' positions 中的所有值互不相同。
解决思路
用一个栈存放当前存活的机器人，按位置从左至右（排序后的下标）遍历机器人并判断当前机器人的方向：
1. 如果当前机器人方向是 R，当前机器人推入栈，继续处理下一个机器人；
2.如果方向是 L:
（1）如果栈为空，当前机器人推入栈，继续处理下一个机器人；
（2） 如果栈顶元素方向也是 L，当前机器人推入栈，继续处理下一个机器人；
（3） 比较与栈顶元素的健康度，判断存活哪个：
- 如果栈顶存活，栈顶机器人健康度减 1，继续处理下一个机器人；
- 如果当前存活，栈顶弹出，当前机器人健康度减 1，回到 2.3 ；
- 如果两个都消失，栈顶弹出，继续处理下一个机器人。
3.最后，按position顺序返回stack 中的健康度即可。
代码（JavaScript）
function survivedRobotsHealths(positions: number[], healths: number[], directions: string) : number[] {
//用一个栈存放当前存活的机器人
let stack: robot[] = [];
interface robot {
i: number;
p: number;
h: number;
d: string;
}
let robots: robot[] = [];
//从左至右（排序后的下标）遍历机器人并判断当前机器人的方向
positions.forEach((v, i) = >robots.push({
i: i,
p: v,
h: healths[i],
d: directions[i]
}));
robots.sort((a, b) = >a.p - b.p);
for (let i = 0; i < robots.length;) {
/**比较与栈顶元素的健康度，判断存活哪个：
1.如果栈顶存活，栈顶机器人健康度减 1，继续处理下一个机器人；
2.如果当前存活，栈顶弹出，当前机器人健康度减 1，回到 2.3 ；
3.如果两个都消失，栈顶弹出，继续处理下一个机器人。**/
if (stack.length === 0 || robots[i].d === 'R' || (robots[i].d === 'L' && stack[stack.length - 1].d === 'L')) {
stack.push(robots[i++]);
} else if (stack[stack.length - 1].h === robots[i].h) {
stack.pop();
i++;
} else if (stack[stack.length - 1].h > robots[i].h) {
stack[stack.length - 1].h--;
i++;
} else if (stack[stack.length - 1].h < robots[i].h) {
stack.pop();
robots[i].h--;
}
}
// console.log(stack);
stack.sort((a, b) => a.i - b.i); let ans = []; stack.forEach(v=> ans.push(v.h)); return ans;
};
最低票价
问题：
在一个火车旅行很受欢迎的国度，你提前一年计划了一些火车旅行。在接下来的一年里，你要旅行的日子将以一个名为 days 的数组给出。 每一项是一个从 1 到 365 的整数。
火车票有 三种不同的销售方式 ：
- 一张 为期一天 的通行证售价为 costs[0] 美元；
- 一张 为期七天 的通行证售价为 costs[1] 美元；
- 一张 为期三十天 的通行证售价为 costs[2] 美元。
通行证允许数天无限制的旅行。 例如，如果我们在第 2 天获得一张 为期 7 天 的通行证，那么我们可以连着旅行 7 天：第 2 天、第 3 天、第 4 天、第 5 天、第 6 天、第 7 天和第 8 天。 返回 你想要完成在给定的列表 days 中列出的每一天的旅行所需要的最低消费 。
示例 1：
输入：days = [1,4,6,7,8,20], costs = [2,7,15]
输出：11
解释： 例如，这里有一种购买通行证的方法，可以让你完成你的旅行计划： 在第 1 天，你花了 costs[0] = $2 买了一张为期 1 天的通行证，它将在第 1 天生效。 在第 3 天，你花了 costs[1] = $7 买了一张为期 7 天的通行证，它将在第 3, 4, ..., 9 天生效。 在第 20 天，你花了 costs[0] = $2 买了一张为期 1 天的通行证，它将在第 20 天生效。 你总共花了 $11，并完成了你计划的每一天旅行。
示例 2：
输入：days = [1,2,3,4,5,6,7,8,9,10,30,31], costs = [2,7,15]
输出：17
解释： 例如，这里有一种购买通行证的方法，可以让你完成你的旅行计划： 在第 1 天，你花了 costs[2] = $15 买了一张为期 30 天的通行证，它将在第 1, 2, ..., 30 天生效。 在第 31 天，你花了 costs[0] = $2 买了一张为期 1 天的通行证，它将在第 31 天生效。 你总共花了 $17，并完成了你计划的每一天旅行。
提示：
- 1 <= days.length <= 365
- 1 <= days[i] <= 365
- days 按顺序严格递增
- costs.length == 3
- 1 <= costs[i] <= 1000
解决思路
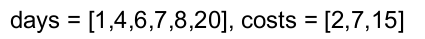
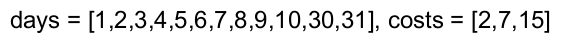
代码（JavaScript）
1.暴力递归解法：
//暴力递归解法
function mincostTickets(days: number[], costs: number[]) : number {
return costday(days, costs, 1);
};
function costday(days: number[], costs: number[], day: number) : number {
if (day > days[days.length - 1]) {
return 0;
}
if (day == days[days.length - 1]) {
return Math.min(...costs);
}
if (!days.includes(day)) {
return costday(days, costs, day + 1);
} else {
return Math.min( costday(days, costs, day + 1) + costs[0], costday(days, costs, day + 7) + costs[1], costday(days, costs, day + 30) + costs[2], )
}
};
问题：
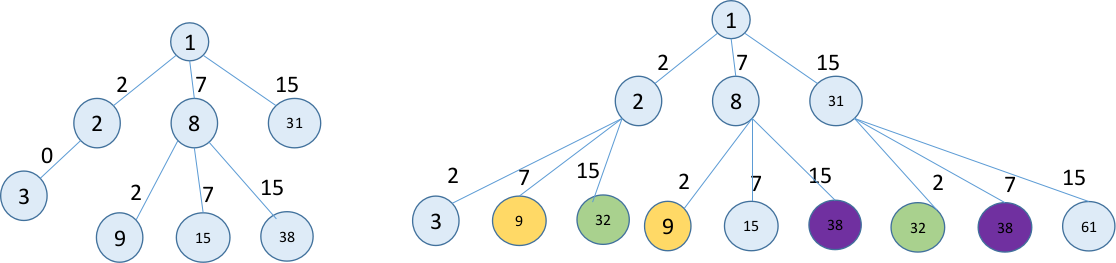
此解法存在重叠子问题和最优子结构
重叠子问题就是F(n)会重复计算，上图中同色的结点
最优子结构就是F(n)的解，可以由子问题F(n+1),F(n+7),F(n+30)的解得到
解决方案：
记录每个子问题f(n)的解，如果后面的计算又要用f(n)，则直接取计算结果，避免重复计算：
function mincostTickets(days: number[], costs: number[]) : number {
let fn = [];
return costday(days, costs, 1, fn);
};
function costday(days: number[], costs: number[], day: number, fn: number[]) : number {
if (day > days[days.length - 1]) {
return 0;
}
if (day == days[days.length - 1]) {
if (!fn[day]) { fn[day] = Math.min(...costs);
}
return fn[day];
}
if (!days.includes(day)) {
if (!fn[day]) { fn[day] = costday(days, costs, day + 1, fn);
}
return fn[day];
} else {
if (!fn[day]) { fn[day] = Math.min( costday(days, costs, day + 1, fn) + costs[0], costday(days, costs, day + 7, fn) + costs[1], costday(days, costs, day + 30, fn) + costs[2], )
}
return fn[day];
}
};
2.动态规划，自底向上解法
将前面的F(n)换为dp[n]，表示从第n天开始后，总共的花费，dp[1]即是问题的解，F(n)是从前往后算，dp是从后往前算，消除递归。
function mincostTickets(days: number[], costs: number[]) : number {
const lastDay = days[days.length - 1];
let dp = new Array(lastDay + 30 + 1).fill(0);
for (let i = lastDay; i >= 1; i--) {
if (days.includes(i)) {
//此处还可以优化，将所有days放到set中判断day是否存在
dp[i] = Math.min(dp[i + 1] + costs[0], dp[i + 7] + costs[1], dp[i + 30] + costs[2]);
} else {
dp[i] = dp[i + 1];
}
}
return dp[1];
};
总结
以上就是机器人碰撞和最低票价两个问题的解法，除此之外，如果您想了解更多关于JavaScript的资料，欢迎访问这篇学习指南，无论是初学者还是有经验的专业人士，该帮助手册都将为您提供有价值的指导和帮助。
扩展链接：
