图
1.学习总结(2分)
1.1图的思维导图

1.2 图结构学习体会
深度遍历算法
其利用深度优先搜索算法可以产生目标图的相应拓扑排序表,利用拓扑排序表可以方便的解决很多相关的图论问题,如最大路径问题等等。
广度遍历算法
广度优先遍历是连通图的一种遍历策略。因为它的思想是从一个顶点V0开始,辐射状地优先遍历其周围较广的区域,
Prim和Kruscal算法
Prim算法:就是点优先,原始集合里面存放所有的点,目标集合最初为空,先任意从原始集合取一个点放在目标集合,此时开始搜索,原始集合到目标集合最近的一个点,找到后将他放入目标集合,更新原始集合中的点到目标集合的距离,一直将原始集合中的点全部加入到目标集合中,完成搜索。
Kruskal算法:就是边优先,先将每一条边从大到小排序,每次去最小的一条边连接两个点,但是需要判断,是否形成回路。
Dijkstra算法
Dijkstra算法一般的表述通常有两种方式,一种用永久和临时标号方式,一种是用OPEN, CLOSE表的方式,这里均采用永久和临时标号的方式。注意该算法要求图中不存在负权边。
拓扑排序算法
对一个有向无环图G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边(u,v)∈E(G),则u在线性序列中出现在v之前
2.PTA实验作业(4分)
2.1 题目1:7-1 图着色问题
2.2 设计思路(伪代码或流程图)
2.3 代码截图

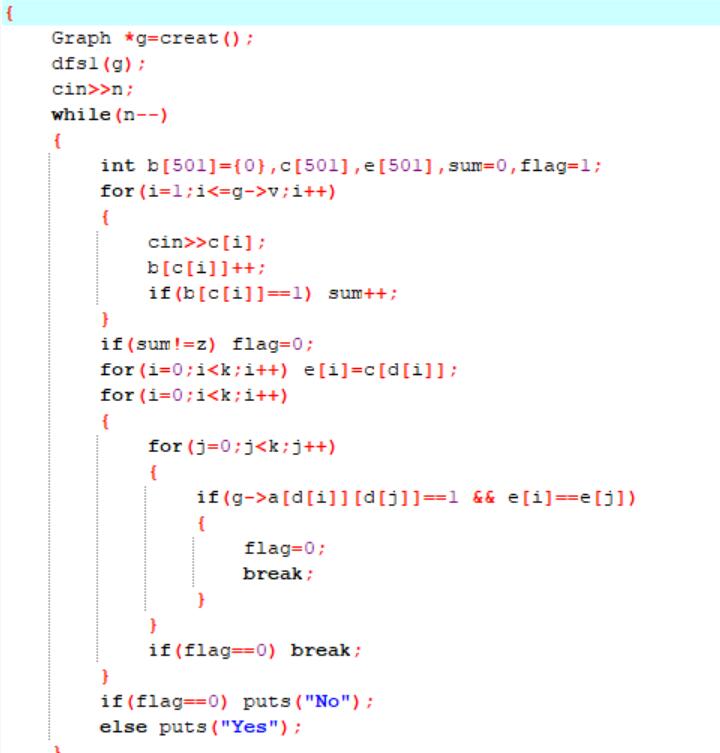
2.4 PTA提交列表说明。

一开始因为自己的疏忽 没有事先在Dev上很好的运行,导致基础的编译错误,理解问题以后仔细检查之后发现是非常不应该的错误,改正以后得以解决。
2.1 7-2 排座位
2.2 设计思路(伪代码或流程图)
2.3 代码截图
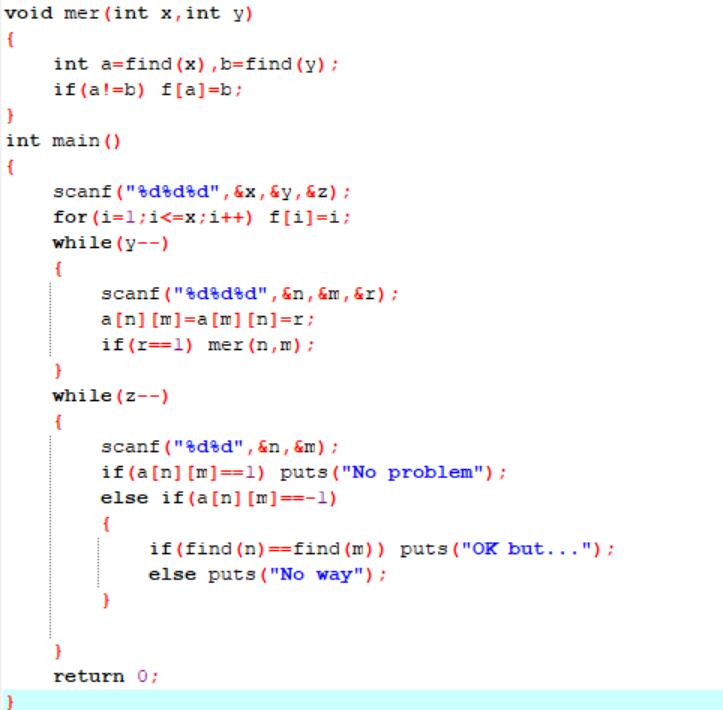
2.4 PTA提交列表说明。

一开始因为自己的疏忽 没有事先在Dev上很好的运行,没有全面考虑问题,理解问题以后仔细检查之后发现是非常不应该的错误,改正以后得以解决。
2.1 题目1:7-4 公路村村通
2.2 设计思路(伪代码或流程图)
2.3 代码截图

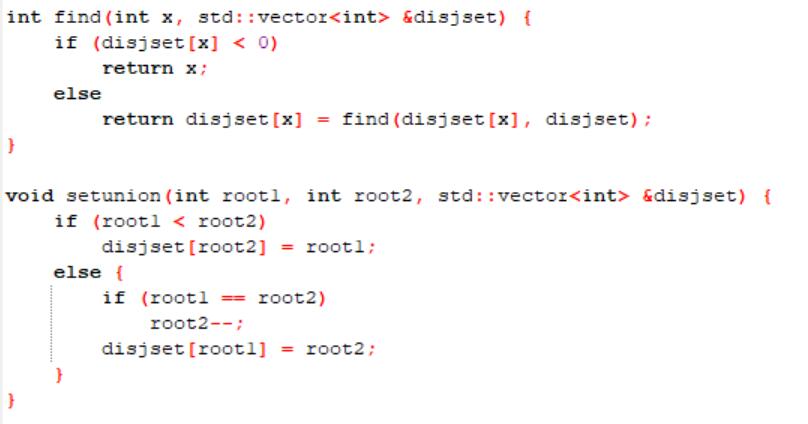
2.4 PTA提交列表说明。

一开始因为自己的疏忽 没有事先在Dev上很好的运行,导致基础的编译错误,理解问题以后仔细检查之后发现是非常不应该的错误,改正以后得以解决。
3.截图本周题目集的PTA最后排名(3分)
3.1 PTA排名(截图带自己名字的排名)

3.2 我的总分:
200
4. 阅读代码(必做,1分)
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <time.h>
#define MAXVEX 6 // 最大顶点数
#define INF 65535
typedef int Status; //Status是函数的类型,其值是函数结果状态代码,如OK等
typedef char VertexType; //顶点类型
typedef int EdgeType; // 边上的权值类型
typedef struct
{
VertexType vexs[MAXVEX]; //顶点表
EdgeType arc[MAXVEX][MAXVEX];//邻接矩阵,可看作边表
int numNodes, numEdges; // 图中当前的顶点数和边数
}MGraph;
// 建立无向网图的邻接矩阵表示
void CreateMGraph(MGraph *G)
{
int i,j,k,w;
printf("输入顶点数和边数:\n");
scanf("%d,%d",&G->numNodes,&G->numEdges); // 输入顶点数和边数
for(i = 0;i <G->numNodes;i++) // 读入顶点信息,建立顶点表
scanf("%c",&G->vexs[i]);
for(i = 0;i <G->numNodes;i++)
for(j = 0;j <G->numNodes;j++)
G->arc[i][j]=INF; // 邻接矩阵初始化
for(k = 0;k <G->numEdges;k++) // 读入numEdges条边,建立邻接矩阵
{
printf("输入边(vi,vj)上的下标i,下标j和权w:\n");
scanf("%d,%d,%d",&i,&j,&w); // 输入边(vi,vj)上的权w
G->arc[i][j]=w;
G->arc[j][i]= G->arc[i][j]; //因为是无向图,矩阵对称
}
}
int main(void)
{
MGraph G;
CreateMGraph(&G);
return 0;
}
#include<stdio.h>
#include<iostream.h>
#define MAXVEX 100 //最大顶点数
typedef char VertexType; //顶点类型应由用户定义
typedef int EdgeType; //边上的权值类型应由用户定义
typedef struct EdgeNode//边表结点
{
int adjvex;//邻接点域,存储该顶点对应的下标
EdgeType weight;//用于存储权值,对于非网图可以不需要
struct EdgeNode *next; //链域,指向下一个邻接点
} EdgeNode;
typedef struct VextexNode//顶点表结点
{
VertexType data;//顶点域,存储顶点信息
EdgeNode *firstedge;//边表头指针
} VextexNode, AdjList[MAXVEX];
typedef struct
{
AdjList adjList;
int numNodes, numEdges; // 图中当前顶点数和边数
} GraphAdjList;
voidCreateALGraph(GraphAdjList *Gp)
{
int i, j, k;
EdgeNode *pe;
printf("输入顶点数和边数(空格分隔):");
scanf("%d%d",&Gp->numNodes,&Gp->numEdges);
for (i = 0 ; i < Gp->numNodes; i++)
{
printf("输入顶点信息:");
scanf("%c",&Gp->adjList[i].data);
Gp->adjList[i].firstedge = NULL;//将边表置为空表
}
for (k = 0; k < Gp->numEdges; k++)//建立边表
{
printf("输入边(vi,vj)的顶点序号i,j(空格分隔:");
scanf("%d%d",&i,&j);
pe = (EdgeNode*)malloc(sizeof(EdgeNode));
pe->adjvex = j;//邻接序号为j
//将pe的指针指向当前顶点上指向的结点
pe->next =Gp->adjList[i].firstedge;
Gp->adjList[i].firstedge = pe;//将当前顶点的指针指向pe
pe = (EdgeNode*)malloc(sizeof(EdgeNode));
pe->adjvex = i;
pe->next =Gp->adjList[j].firstedge;
Gp->adjList[j].firstedge = pe;
}
}
int main(void)
{
GraphAdjList GL;
CreateALGraph(&GL);
return 0;
}
pim算法和Kruskal两种实现方法
#include<stdio.h>
int arr[101][101];
int main()
{
int n,ttt = 0;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
scanf("%d",&arr[i][j]);
}
}
for(int j=2;j<=n;j++)
{
int min = 100000000;
int index = 0;
for(int i=1;i<=n;i++)
{
if(arr[1][i]==0) continue;
if(arr[1][i]<min)
{
min = arr[1][i];
index = i;
}
}
ttt += arr[1][index];
for(int i=1;i<=n;i++)
{
arr[1][i] =arr[1][i]<arr[index][i]?arr[1][i]:arr[index][i];
}
}
printf("%d\n",ttt);
return 0;
}
#include <stdio.h>
#include <stdlib.h>
#define MAX_VEX_NUM 50
#define MAX_ARC_NUM 100
#define UN_REACH 1000
typedef char VertexType;
typedef enum
{
DG, UDG
}GraphType;
typedef struct
{
VertexType vexs[MAX_VEX_NUM];
int arcs[MAX_VEX_NUM][MAX_VEX_NUM];
int vexnum, arcnum;
GraphType type;
}MGraph;
/**
* 根据名称得到指定顶点在顶点集合中的下标
* vex 顶点
* return 如果找到,则返回下标,否则,返回0
*/
int getIndexOfVexs(char vex,MGraph *MG)
{
int i;
for (i = 1; i <= MG->vexnum; i++)
{
if (MG->vexs[i] == vex)
{
return i;
}
}
return 0;
}
/**
* 创建邻接矩阵
*/
void create_MG(MGraph *MG)
{
int i, j, k,weight;
int v1, v2, type;
char c1, c2;
printf("请输入图类型DG(0)和图(1) :");
scanf("%d", &type);
if (type == 0)
MG->type = DG;
else if (type == 1)
MG->type = UDG;
else
{
printf("请输入正确的图形类型DG(0)和图(1)");
return;
}
printf("请输入vexmun : ");
scanf("%d", &MG->vexnum);
printf("请输入 arcnum :" );
scanf("%d", &MG->arcnum);
getchar();
for (i = 1; i <= MG->vexnum; i++)
{
printf("请输入 %dth vex(char):", i);
scanf("%c",&MG->vexs[i]);
getchar();
}
//初始化邻接矩阵
for (i = 1; i <= MG->vexnum; i++)
{
for (j = 1; j <= MG->vexnum; j++)
{
if(i == j)
MG->arcs[i][j] = 0;
else
MG->arcs[i][j] = UN_REACH;
}
}
//输入边的信息,建立邻接矩阵
for (k = 1; k <= MG->arcnum; k++)
{
printf("请输入 %dth arc v1(char) v2(char) weight(int):", k);
scanf("%c %c %d", &c1,&c2,&weight);
v1 = getIndexOfVexs(c1, MG);
v2 = getIndexOfVexs(c2, MG);
if (MG->type == 1)
MG->arcs[v1][v2] =MG->arcs[v2][v1] = weight;
else
MG->arcs[v1][v2] = weight;
getchar();
}
}
/**
* 打印邻接矩阵和顶点信息
*/
void print_MG(MGraph MG)
{
int i, j;
if(MG.type == DG)
{
printf("Graph type: Directgraph");
}
else
{
printf("Graph type: Undirectgraph");
}
printf("图的顶点数: %d,MG.vexnum");
printf("图弧数: %d,MG.arcnum");
printf("Vertex set:");
for (i = 1; i <= MG.vexnum; i++)
printf("%c", MG.vexs[i]);
printf("邻接矩阵:");
for (i = 1; i <= MG.vexnum; i++)
{
j = 1;
for (; j < MG.vexnum; j++)
{
printf("%d", MG.arcs[i][j]);
}
printf("%d", MG.arcs[i][j]);
}
}
// 定义边结构体
typedef struct
{
int start;
int end;
int cost;
}Edge;
/* *
* 由邻接矩阵得到边的信息
*
* */
void init_edge(MGraph MG,Edgeedge[])
{
int i,j;
int count = 0;
if(MG.type == 0)
{
for(i = 1; i <= MG.vexnum;i++)
{
for (j = 1;j <= MG.vexnum;j++)
{
if(MG.arcs[i][j] != 0&& MG.arcs[i][j] != UN_REACH)
{
edge[count].start = i;
edge[count].end = j;
edge[count].cost =MG.arcs[i][j];
count++;
}
}
}
}
else
{
for(i = 1; i <= MG.vexnum;i++)
{
for (j = i;j <= MG.vexnum;j++)
{
if(MG.arcs[i][j] != 0 &&MG.arcs[i][j] != UN_REACH)
{
edge[count].start = i;
edge[count].end = j;
edge[count].cost =MG.arcs[i][j];
count++;
}
}
}
}
}
/* *
* 将边按权值从大到小排序
* */
void sort_edge(Edge edge[],intarcnum)
{
int i,j;
Edge temp;
for(i = 0; i < arcnum - 1;i++)
{
for (j = i+1;j < arcnum;j++)
{
if(edge[i].cost > edge[j].cost)
{
temp = edge[i];
edge[i] = edge[j];
edge[j] = temp;
}
}
}
}
/* *
* 输出边的信息
* */
void print_edge(Edgeedge[],int arcnum)
{
int i = 0;
while(i < arcnum)
{
printf("%d,%d,%d",edge[i].start,edge[i].end,edge[i].cost);
i++;
}
}
/**
* 找出指定节点的所属的连通分量,这里是找出其根节点在father数组中下标。
**/ int findFather(intfather[],int v)
{
int t = v;
while(father[t] != -1)
t = father[t];
return t;
}
/* *
*Kruskal算法求最小生成树
* */
void Kruskal_MG(MGraph MG,Edgeedge[])
{
int father[MAX_VEX_NUM];
int i,count,vf1,vf2;
// 初始化father数组
for(i = 0;i < MAX_VEX_NUM;i++)
{
father[i] = -1;
}
i = 0;
count = 0; // 统计加入最小生树中的边数
// 遍历任意两个结点之间的边
while(i < MG.arcnum && count< MG.arcnum)
{
vf1 = findFather(father,edge[i].start);
vf2 = findFather(father,edge[i].end);
// 如果这两个节点不属于同一个连通分量,则加入同一个连通分量
if (vf1 != vf2)
{
father[vf2] = vf1;
count++;
printf("%c,%c,%d",MG.vexs[edge[i].start],MG.vexs[edge[i].end],edge[i].cost);
}
i++;
}
}
/**
* 主函数
*/
int main(void)
{
MGraph MG;
Edge edge[MAX_ARC_NUM];
create_MG(&MG);
print_MG(MG);
init_edge(MG,edge);
sort_edge(edge,MG.arcnum);
printf("the result of Kruskal:");
Kruskal_MG(MG,edge);
return EXIT_SUCCESS;
}




