并查集

　　并查集是一种使用树形结构处理集合问题的数据结构，从它的名字可以看出，并查集支持集合的合并、集合的查询两种功能。并查集的概念很好理解，下面对并查集进行简单举例。

　　一个学校有10名学生，学生的学号分别从1~10，这10名学生被随机分在了4个 班，具体分班情况如下：

　　0号班：学号为1、3、4的 学生，

　　1号班：学号为2、5、6、7、8的学生，

　　2号班：学号为10的学生，

　　3号班：学号为9的学生。

为了对以上分班情况进行存储，可以使用数组f对其进行记录：

0

1

0

0

1

1

1

1

3

2

 

　　在上面，数组元素f[1] = 0，表示1号同学属于0班，f[2] = 1,表示2号同学属于1班，以此类推。我们可以发现，我们使用了数组下标用来表示学号，数组下标对应的元素用来存储该学生所在的班级编号。记录存储过程的数组实现过程如下：

　　

const int MAX = 1001;
int f[MAX];

 

　　此时，如果要对0号班级和1号班级的学生进行合并，只需要遍历一遍数组将全部的1改为0或者将全部的0改为1。这个操作的时间复杂度为O(n)，这是一个很慢的速度，从构建数据结构的角度出发，可以对其进行优化。

　　我们在脑海中，将原本学生与班级之间的隶属关系从线性结构转化为二维树形结构，父亲节点为班级编号，儿子节点为学生编号。此时，对于10名学生和4个班级之间的关系，可以转化为如下形式：

　　

　　

　　当要求将0班和1班合并，只需将0节点变成1节点的儿子节点，合并操作由于只需要设置父子关系，因此时间复杂度为O(1)，合并后如下：

　　

 

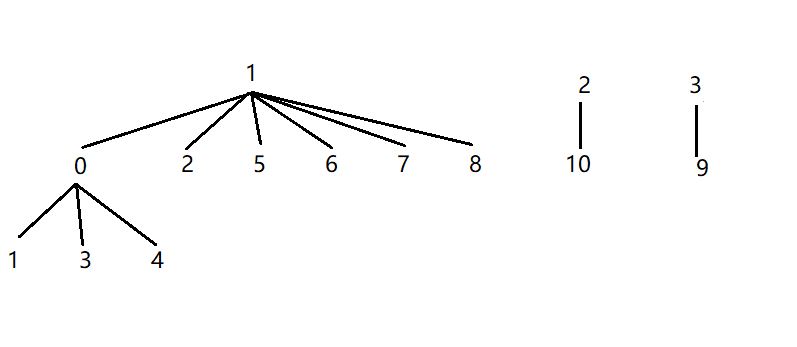
　　当要求对所属集合进行查询时，只需沿着父亲不断找到根。比如说要求查询合并后4号学生所属班级，查询过程为：先找到4号学生的父亲节点0班，再找到0班的父亲节点1班，所以4号学生属于1班。由于查询过程需要不断往上查找根，因此时间复杂度为O(N)，查询操作的此处可以进一步优化。我们使用路径压缩来对查询过程进行优化。所谓路径压缩，是指在查找根时同时更新路径上所有节点的根，这样可以使得均摊时间复杂度降低至O(1)。我们使用递归来完成这一操作，递归实现过程如下：

　　

void findF(int now)
{
    if(f[now] == now) return now;
    f[now] = findF(f[now]);　　//更新路径上的节点
    return f[now];
}

　　

　　上面提到的集合合并操作实现过程如下：

　　

void  mergeS(int x, int y)   
{
    int fx = findF(x);   //x的父亲节点       
    int fy = findF(y);   //y的父亲节点
    f[fx] = fy;     //将x所在的集合合并到y所在的集合下面
}

 　　

　　特别说明，一定要理解下面的两条概念：

　　（1）f[now]用于记录学号为now的学生所属的班级！

　　（2）findF(now)函数返回学号为now的学生所属的班级！

 

 

　　完美结束。