LeetCode----跳跃游戏Ⅱ「动态规划」

题目描述

给定一个非负整数数组，你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
你的目标是使用最少的跳跃次数到达数组的最后一个位置。

示例

输入: [2,3,1,1,4]
输出: 2

解释:

跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

说明:

假设你总是可以到达数组的最后一个位置。

思路

脑子直接跳出dp，dp[i] = Min(dp[i-1], ???)
想想又不太对，假如 dp[i] 表示到第 i 个位置的最少步数
但是又不能判断 dp[i+1] 是否可以使用 dp[i] 的步数达到
那咋办嘛。再整个数组存可以到的最大步数呗。。。
长度为 n 的数组，最多可以花 n-1 步到达终点，2个数组长度一致
可以继续优化，时间上：当达到终点可以不用继续遍历；
空间上：可以减少辅助数组的使用，这么多数组只是便于理解，实际存在浪费的问题

演示？

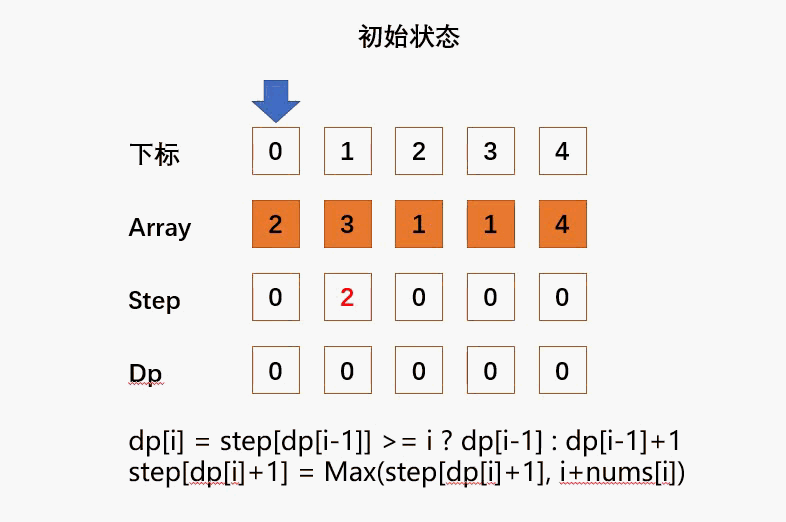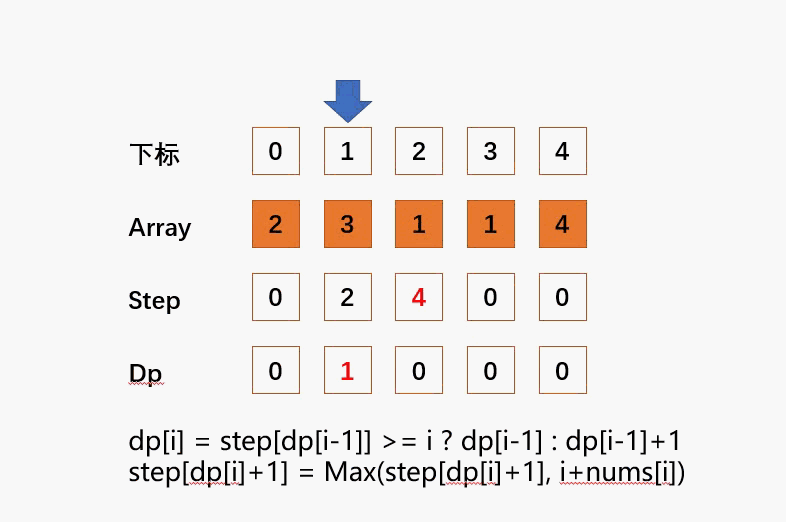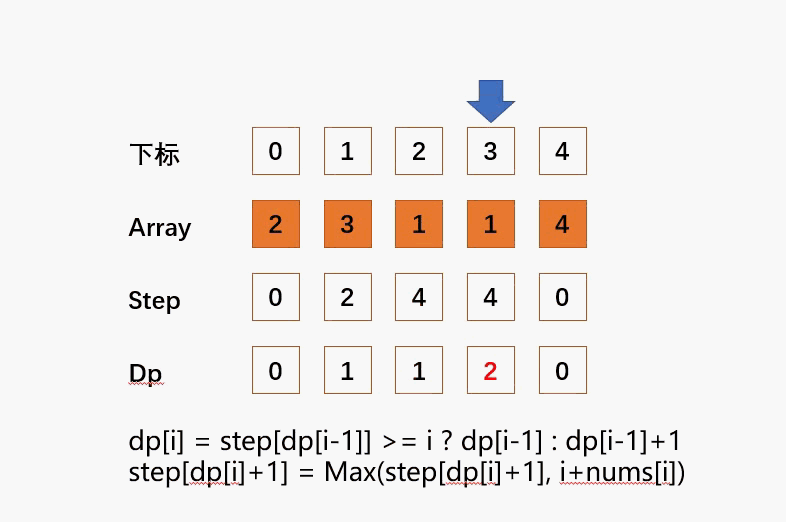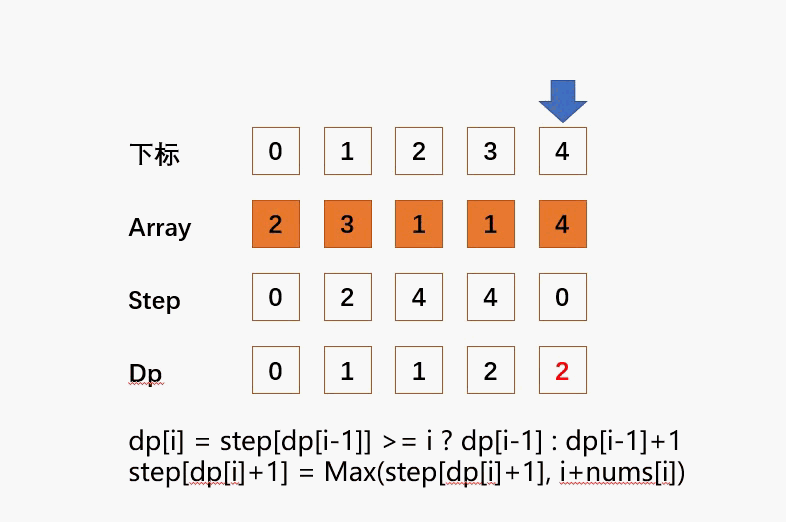
代码

class Solution {
    public int jump(int[] nums) {
        if(nums.length == 1) return 0;  // 一个格子跳啥了还
        int[] step = new int[nums.length], dp = new int[nums.length];
        step[1] = nums[0];  // 第一步可以达到的最大位置，前面已经保证至少 2 格
        for(int i = 1; i < nums.length; ++i) {
            dp[i] = step[dp[i-1]] >= i ? dp[i-1] : dp[i-1]+1;
            // 假如前一个格子所花的步数能达到的最大位置 >= 当前位置，即前一个步数也可以到当前位置
            // 不能到达。不能到达就再走一步！
            if(dp[i]+1 < nums.length)  // 步数可能溢出，但是溢出的数据是没有意义的（一定可以在 n-1 步到达终点）
                step[dp[i]+1] = Math.max(step[dp[i]+1], i+nums[i]);
                // 这里计算的是从当前格子在走一步所能到达的最大距离
                // 假如超过之前存储的最大步数，则更新
        }
        return dp[nums.length-1];
    }
}