树 (tree)

非空树只有一个根，树的各节点互不相交。

degree == 0, 为 leaf. child, parent, sibling.

各子树不能交换，称之为有序树，否则为无序树。

 

小结：

根节点：唯一，无双亲。

叶节点：无孩子，可以多个。

中间节点：一个双亲，多个孩子。

 

双亲表示法：

typedef int treeElement;

typedef struct PTNode { //node structure
    treeElement data;
    int parent;
}PTNode;

typedef struct {
    PTNode nodes[MAXSIZE];
    int r, n;//根的位置和节点数
}PTree;

又可以根据需要，设置长子域、右兄弟域等等。

将根的双亲地址设为-1

 

孩子表示法：

（多重链表表示法）

 

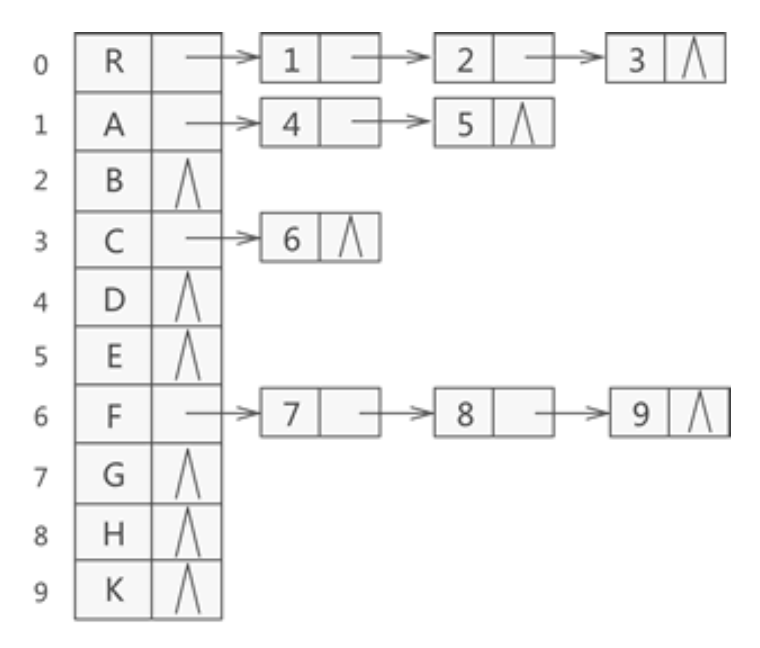
typedef int treeElement;

typedef struct CTNode { //孩子节点单链表形式
    int child;
    struct CTNode* next;
}CTNode;

typedef struct { //表头结构
    treeElement data;
    CTNode* firstchild;
}CTBOX;

typedef struct {
    CTBOX nodes[MAXSIZE];
    int r, n;//根的位置和节点数
}CTree;

可在树结构中添加双亲地址。

 

 

二叉树 (binary tree)

1.左右子树有区别。

2.只有一棵子树也要区分左右。

区分满二叉树、完全二叉树。

 

二叉树性质：

1. i 层上至多有 2^(i-1) 个结点。

2. 深度为 k ，至多有2^k - 1 个结点。

3. n0 = n2 + 1.

4. 具有 n 个结点的二叉树深度为 [log2 n] + 1 。

5. 

 

为节省内存，顺序结构存储完全二叉树。

链二叉树：

typedef struct biNode {
    int data;
    struct biNode* lchild;
    struct biNode* rchild;
}biNode,*biTree;

 

二叉树的遍历算法：

利用递归，实现前序，中序，后序遍历。

区别在于使用结点数值表达式在函数中的位置。

以前序遍历为例：

void preOrderTranverse(biNode* root) {
    if (root == NULL) {
        return;
    }
    printf("%c ", root->data);
    preOrderTranverse(root->lchild);
    preOrderTranverse(root->rchild);
}

 

二叉树的建立：