sklearn决策树特征权重计算方法
训练模型,生成树图
1 from io import StringIO 2 from sklearn.datasets import load_iris 3 from sklearn.tree import DecisionTreeClassifier 4 from sklearn import tree 5 import pydot 6 7 for criterion in ['gini', 'entropy']: 8 clf = DecisionTreeClassifier(criterion=criterion, random_state=0, max_depth=3) 9 iris = load_iris() 10 11 dot_data = StringIO() 12 13 clf.fit(iris.data, iris.target) 14 print(clf.feature_importances_) 15 tree.export_graphviz(clf, out_file=dot_data) 16 graph = pydot.graph_from_dot_data(dot_data.getvalue()) 17 graph[0].write_png('iris_%s.png' % criterion) 18 19 # [ 0. 0. 0.05393633 0.94606367] gini 20 # [ 0. 0. 0.07060267 0.92939733] entropy
gini
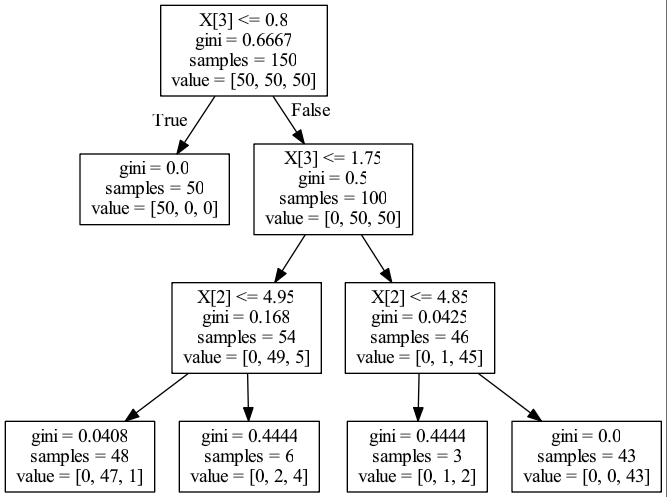
entropy
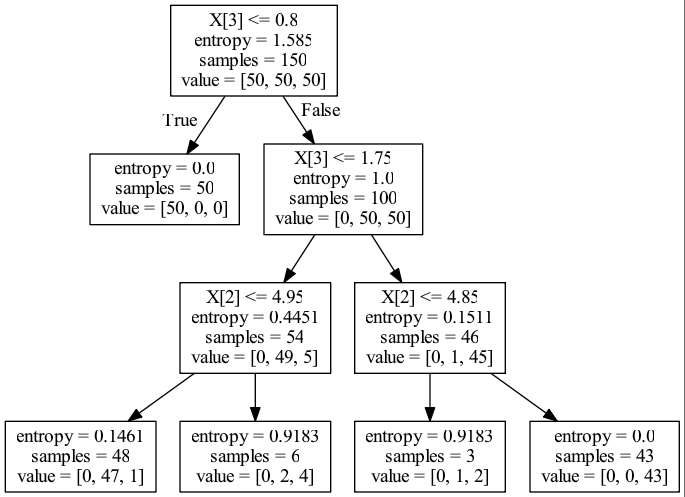
计算 importance,比较和模型生成权重的一致性
import numpy as np def split_gain(gini, n, gini1, n1, gini2, n2, t): return (n*gini - n1*gini1 - n2*gini2)*1.0/t # gini x3_gain = \ split_gain(0.6667, 150, 0, 50, 0.5, 100, 150) + \ split_gain(0.5, 100, 0.168, 54, 0.0425, 46, 150) x2_gain = \ split_gain(0.168, 54, 0.0408, 48, 0.4444, 6, 150) + \ split_gain(0.0425, 46, 0.4444, 3, 0, 43, 150) x = np.array([x2_gain, x3_gain]) x = x / np.sum(x) print('gini:', x) # [ 0.05389858 0.94610142] computed # [ 0.05393633 0.94606367] sklearn x3_gain = \ split_gain(1.585, 150, 0, 50, 1, 100, 150) + \ split_gain(1, 100, 0.4451, 54, 0.1511, 46, 150) x2_gain = \ split_gain(0.4451, 54, 0.1461, 48, 0.9183, 6, 150) + \ split_gain(0.1511, 46, 0.9183, 3, 0, 43, 150) x = np.array([x2_gain, x3_gain]) x = x / np.sum(x) print('entropy:', x) # [ 0.07060873 0.92939127] computed # [ 0.07060267 0.92939733] sklearn
总结
计算特征 对不存度减少的贡献,同时考虑 节点的样本量
对于某节点计算(**criterion可为gini或entropy**)
父节点 有样本量$n_0$,criterion为${c}_0$
子节点1有样本量$n_1$,criterion为${c}_1$
子节点2有样本量$n_2$,criterion为${c}_2$
总样本个数为$T$
$gain = \left(n_0*{c}_0 -n_1*{c}_1-n_2*{c}_2 \right)/T$



