Hamming code

Also known as (7,4) code,7 trainsmitted bits for 4 source code.

 

TRANSMIT

The transmitted procedure can be reprecented as follows.

$t=G^Ts$

where G is:

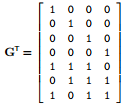
import numpy as np
G = np.matrix(
    [[1,0,0,0],
     [0,1,0,0],
     [0,0,1,0],
     [0,0,0,1],
     [1,1,1,0],
     [0,1,1,1],
     [1,0,1,1]]).T
s=np.matrix([[1,1,1,0]]).T

t = (G.T*s)%2

visualization

 

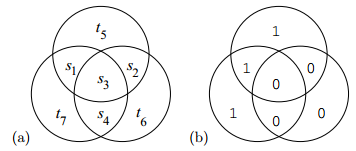
$t_5,t_6,t_7$ is called parity-check bits

----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

DECODING

1.intuitive way: measure the similarity between the recieved bits $r$ and the encoded codes $t$

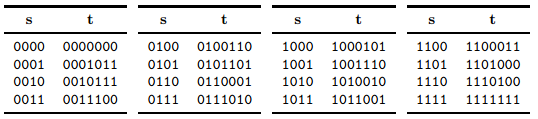
2.Syndrome decoding

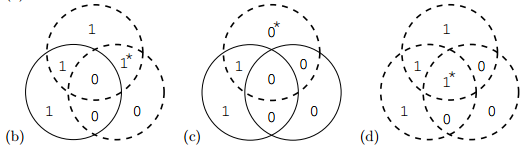
dashed line for which parity is not even(unhappy)

full line for which parity is even(happy)

find the unique bit,that lies inside all unhappy circles and outside all happy circles

the corresponding syndrome z as follow:

(b) 110 ($t_5$ not even,$t_6$ not even,$t_7$ even),$r_2$ should be unflipped

(c) 100 ($t_5$ not even,$t_6$ even,$t_7$ even),$r_5$ should be unflipped

(d) 111 ($t_5$ not even,$t_6$ not even,$t_7$ not even),$r_3$ should be unflipped

all the situations is listed in table below:

the syndrome z can be achieved by matrix:

$z=Hr$

which H is:

----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

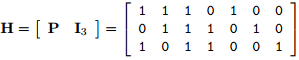
PERFORMANCE

1.when there is only one bit flipped in all 7 bits,the decoder can always get right

2.when there are more than one bits flippend,the decoder get wrong

the single bit error rate，can be estimate as follow：

$p_b \approx \frac{1-{(1-f)}^2-7{(1-f)}^6f}{2}$

the exact error rate is about 0.6688,which can be computed with following program.

 1 import numpy as np
 2 import copy
 3 import itertools
 4 from scipy.misc import comb
 5 
 6 def encode(s):
 7     G = np.array(
 8         [[1,0,0,0],
 9          [0,1,0,0],
10          [0,0,1,0],
11          [0,0,0,1],
12          [1,1,1,0],
13          [0,1,1,1],
14          [1,0,1,1]]
15     )
16 
17     return np.dot(G,s)%2
18 
19 def decode(r):
20     t_hat = copy.deepcopy(r)
21     H = np.array(
22         [[1,1,1,0,1,0,0],
23          [0,1,1,1,0,1,0],
24          [1,0,1,1,0,0,1]]
25     )
26 
27     syndrome_map = {0:-1,
28            1:6,
29            10:5,
30            11:3,
31            100:4,
32            101:0,
33            110:1,
34            111:2}
35 
36     syndrome = np.dot(np.dot(H,r)%2,np.array([100,10,1]))
37     if syndrome_map[syndrome]>=0:
38         t_hat[syndrome_map[syndrome]] = (t_hat[syndrome_map[syndrome]]+1)%2
39 
40     return t_hat
41 
42 def flipn(flip_list,t):
43     '''
44     flipped the bits specified by flip_list and return it
45     :param flip_list:
46     :param t:
47     :return:
48     '''
49     r = copy.deepcopy(t)
50     for flip in flip_list:
51         r[flip] = (r[flip]+1)%2
52     return r
53 
54 def flipn_avg_err(n,s):
55     '''
56     get the average error bits when flip n bits
57     :param n:
58     :param s:
59     :return:
60     '''
61     t = encode(s)
62     items = range(7)
63     errors = 0
64     count = 0
65     for flip in itertools.combinations(items,n):
66         r = flipn(list(flip),t)
67         t_hat = decode(r)
68 
69         errors += 4-sum(s==t_hat[:4])
70         count += 1
71     return errors*1.0/count
72 
73 f = 0.9
74 s = np.array([0,0,0,0])
75 all_error = 0.0
76 for n in range(2,8):
77     error = flipn_avg_err(n,s)
78     all_error += error*comb(7,n)*(f**(7-n))*((1-f)**n)
79 print all_error/4
python
posted @ 2016-01-07 15:41  porco  阅读(743)  评论(0)  编辑  收藏  举报