Chapter 3
-
图像几何变换:包括 空间平移,比例缩放,旋转,仿射变换,图像插值
实质:改变像素的空间位置或估算新空间位置上的像素值
-
图像几何变换的一般表达式:
\[[u,v]=[X(x,y), Y(x,y)] \]常见的三种几何变换:平移、旋转、缩放
线性变换:
- \(f(0)=0\)
- \(f(kx)=kf(x)\)
-
常见变化:
- 线性:拷贝,旋转,放缩
- 非线性:平移,镜像
-
旋转:
-
图像的旋转需要指明绕着哪一个点(原点)旋转
-
一般以图像的几何中心为原点旋转
-
旋转后,图像大小一般会改变
-
-
放大:
为了避免失真,需要使用插值:
-
最近邻插值:即四舍五入
-
双线性插值:
令放大后图像所对应的像素点为\((x,y)\),若放大\((k1,k2)\)倍,则对应原图像素点为\((x/k1,y/k2)\)。
由于\((x/k1,y/k2)\) 不一定是整数,假设其落在四个整数点即\((a,b),(a+1,b),(a,b+1),(a+1,b+1)\) 之间,即
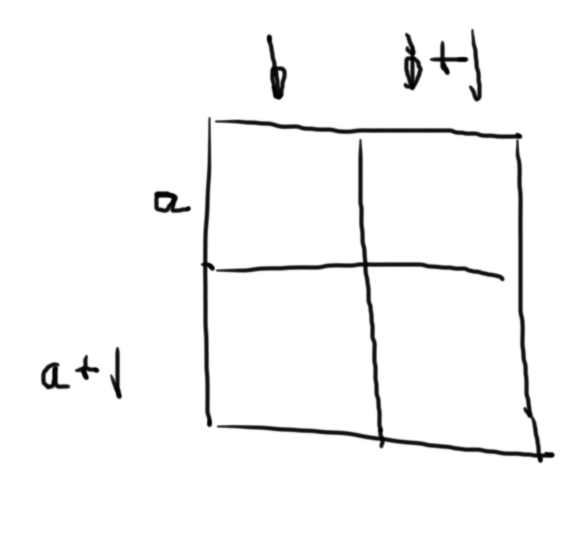
假设横纵方向图像灰度线性变化是线性的,双线性插值依靠加权机制,综合考虑四个像素点的灰度作用。
-
-
错切:
图像的错切变换实际上是平面景物在投影平面上的非垂直投影效果。错切变换也称为剪切、错位或错移变换。
原理:保持图像上各点的某一坐标值不变,而另一坐标值进行线性变换。
坐标不变的轴称为依赖轴,变换的轴称为方向轴。
因为绝大多数图像都是三维物体在二维平面上的投影得到的,所以需要研究图像的错切现象。
下面是错切例子:其中 y 轴为依赖轴,x 轴为方向轴
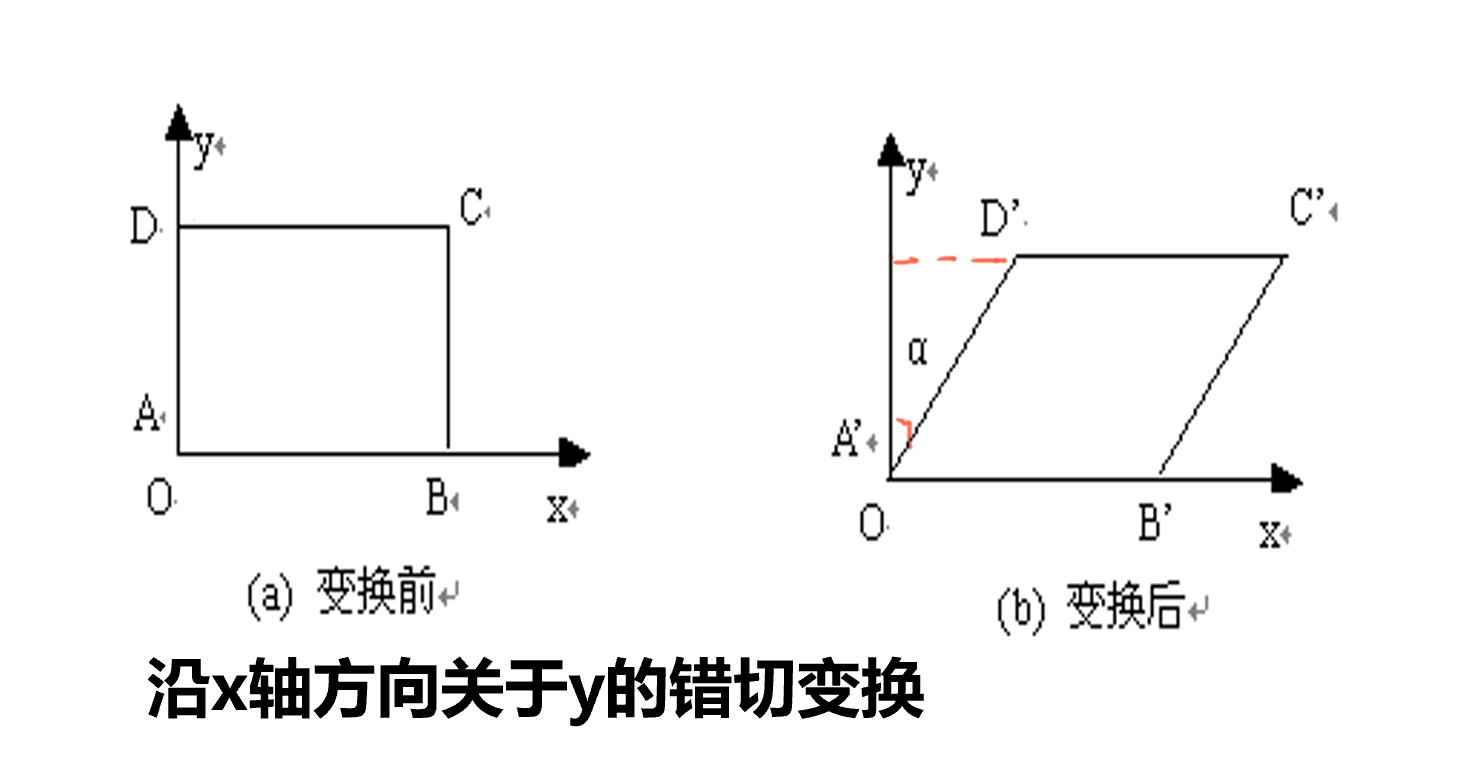
-
\(A_x=0\),\(A_y=0\) 变换到 \(A_x'=A_x + A_y*\tan_\alpha=A_x\),\(A_y'=A_y\)
-
\(D_x=0\),\(D_y=m\) 变换到 \(D_x=D_x+D_y*\tan_\alpha\)
进行错切时,给一个\(\tan_\alpha\) 值,然后指定依赖轴和方向轴,即可进行变换
可以发现,当\(\tan_\alpha\)不为整数时,错切得到的新坐标不一定有意义,可以先计算错切后的画布大小,然后求逆变换结合插值算法。
-
投影
可以根据相似三角形推导



