图 embedding & clustering 相关论文笔记

目录

本文包括了 GCN，GAT 及基于这些模型的 AE 来获取 embedding 和 进行 clustering 相关论文。着重介绍其方法、框架、训练流程、效果。

名称 会议/期刊 时间
Variational Graph Auto-Encoders NIPS 2016
Adversarially Regularized Graph Autoencoder for Graph Embedding 2019.1
Attributed Graph Clustering: A Deep Attentional Embedding Approach IJCAI 2019.1
Graph Attention Auto-Encoders 2019.5.26
Graph embedding clustering: Graph attention auto-encoder with cluster-specificity distribution 2021.5
Self-supervised graph convolutional clustering by preserving latent distribution 2021

1 Variational Graph Auto-Encoders（VGAE，GAE）

本文只介绍图自编码器部分，不介绍变分图自编码器。

1.1 编码器

编码器部分为一个二层GCN，原始图的邻接矩阵 \(A\) 和节点特征矩阵 \(X\) 被送入 \(GCN\) ，网络输出节点 embedding 矩阵 \(Z\) ：

\[Z = GCN(X,A) \]

1.2 解码器

这里解码器与编码器并非完全对称的结构，即并非将 embedding 再经过两层 \(GCN\) 得到一个与输入特征同纬度的节点特征矩阵\(\hat{X}\)，并考虑 \(\hat{X}\) 对 \(X\) 的重构（有的模型是这么做的，本文后面会提到），而是简单将 \(Z\) 乘以自身转置，以计算节点间相似度：

\[\hat{A} = sigmoid(ZZ^T) \]

将节点间相似度看作两个节点间存在边的概率，以此衡量重构图和原始图之间的差异，从而计算重构误差：

\[L = E_{q(Z|X,A)}[\log p(A|Z)] \]

上式本质上是计算 \(A\) 和 \(\hat{A}\) 的交叉熵。

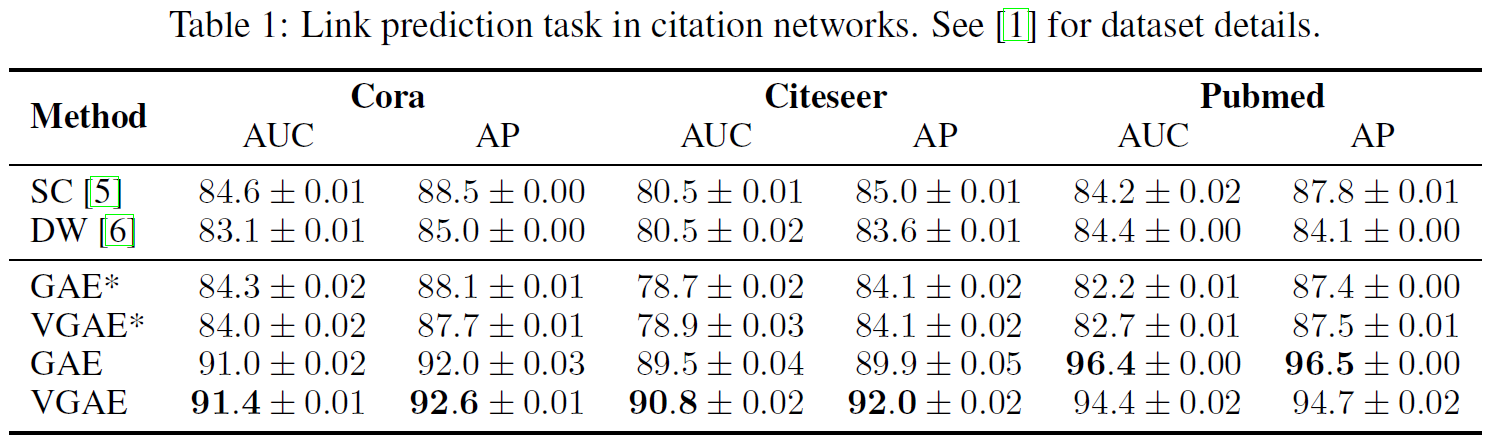
1.3 实验结果

* 代表不使用节点特征矩阵 \(X\) ，仅考虑图结构信息 \(A\) 。

image-20210730121500202

2 Adversarially Regularized Graph Autoencoder for Graph Embedding （ARGA，ARVGA）

本文在GAE的基础上增添了一个对抗模型，总体称为ARGA；如果引入变分机制，则为在VGAE的基础上增添对抗模型，整体称为ARVGA。本文同样不介绍变分的部分，只介绍 ARGA。

2.2 问题定义

  • 图

    一个图被表示为 \(G = \{V,E,X\}\) ，\(V\) 为节点集合 \(V=\{v_i\}_{i=1...n}\)，\(E\) 为边集合，每一个元素都是一个二元组 \(e_{i,j}=<v_i,v_j> \in E\) 根据 \(V,E\) 可以构造图 \(G\) 的邻接矩阵 \(A\) ，这是一个 \(01-\)矩阵， \(A_{ij}=1 \ \ \ \iff \ \ \ e_{i,j} \in E\) 。 矩阵 \(X \in \R^{N\times F}\)，表示着每一个节点的初始特征。

  • 图 embedding

    给定一个图 \(G\)， 我们的任务是将每一个节点 \(v_i \in V\) 的特征从 \(\R^{F}\) 映射到一个低维空间 \(\R^d\)。即需要构造一个函数 \(f\)，完成 \(f:(A,X) \to Z\)，其中 \(z_i^T\) 是矩阵 \(Z \in \R^{n\times d}\) 的第 \(i\) 行。我们将 \(Z\) 称为 embedding 矩阵，期望这个 embedding 可以重构拓扑结构 \(A\) 和节点特征矩阵 \(X\) 。

2.2 整体框架

包含两部分

  1. 自编码模型

    自编码模型接受图的拓扑结构信息 \(A\) 及节点特征信息 \(A\)，经过两层 \(GCN\) 得到 embedding 矩阵 \(Z\)，并使用 \(Z\) 重构 \(A\)。

  2. 对抗模型

    对抗模型强制潜变量尽可能匹配先验分布 ，该模块用于判断当前潜变量是来自于编码器得到的 embedding 矩阵 \(Z\) 还是先验分布（本文假设为高斯分布）所产生的噪声。

整个框架图如下：

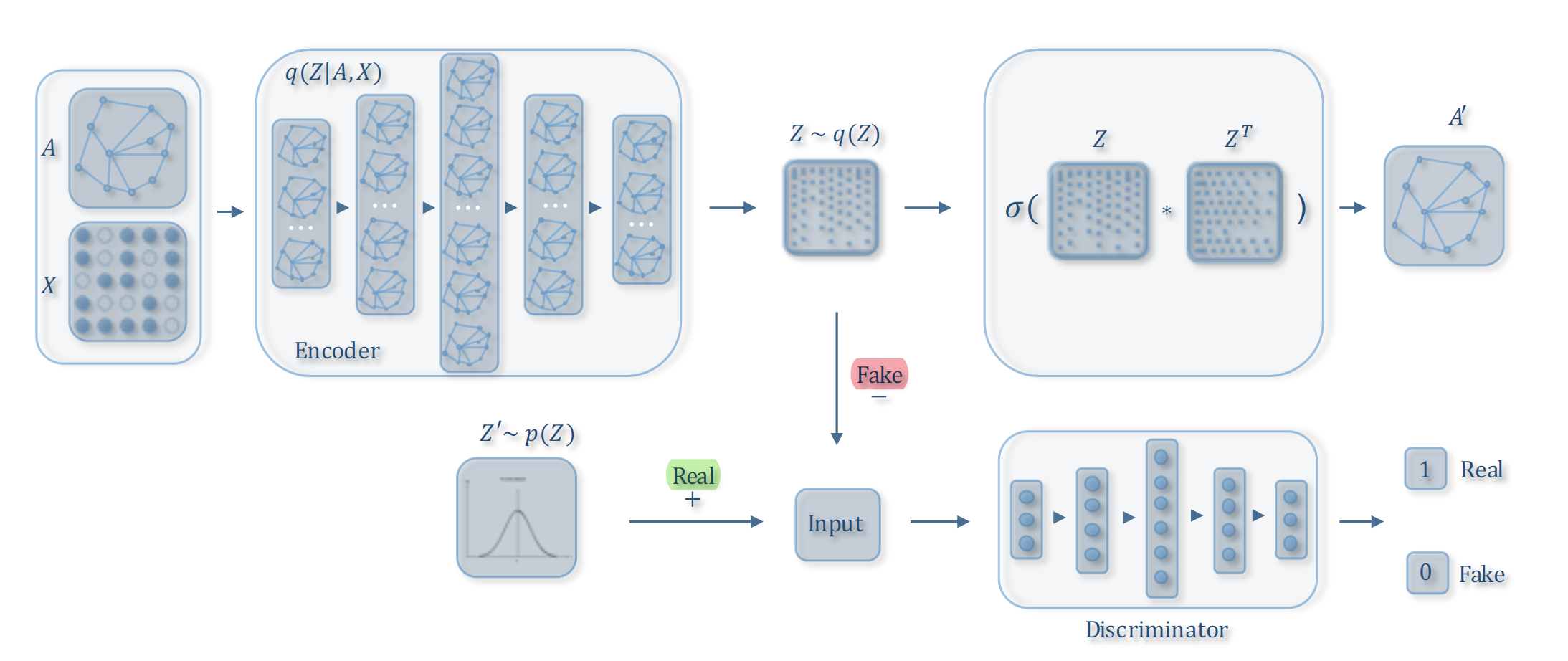
image-20210730205837864

2.2.1 自编码模型

这一部分与GAE完全相同

2.2.2 对抗模型

我们将先验分布产生的高斯噪声视作真实样本，将 embedding 视作 虚假样本，利用判别器强制使得 embedding 匹配先验分布，以使 embedding 满足高斯分布。这是一种 VAE-GAN 的思想。需要注意的是，\(Z'\) 来自于 \(GCN-1\) 的输出 \(+\) 高斯噪声 ， \(Z\) 来自于 \(GCN-2\) 的输出，二者维度不一定相同，因此判别器在对二者进行判别时，需要各自经过两个输入维度不同的 \(MLP\)，最终输出一个实数来代表分数 \(R\) 。

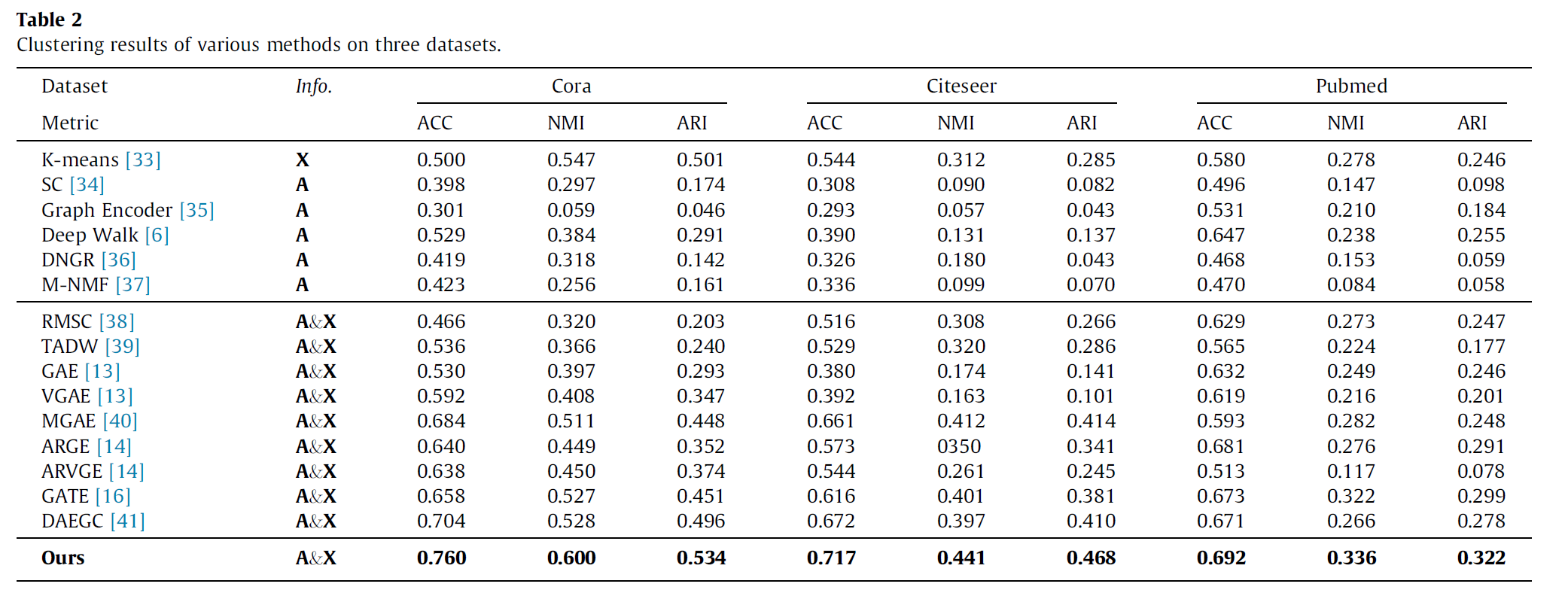
2.3 实验结果

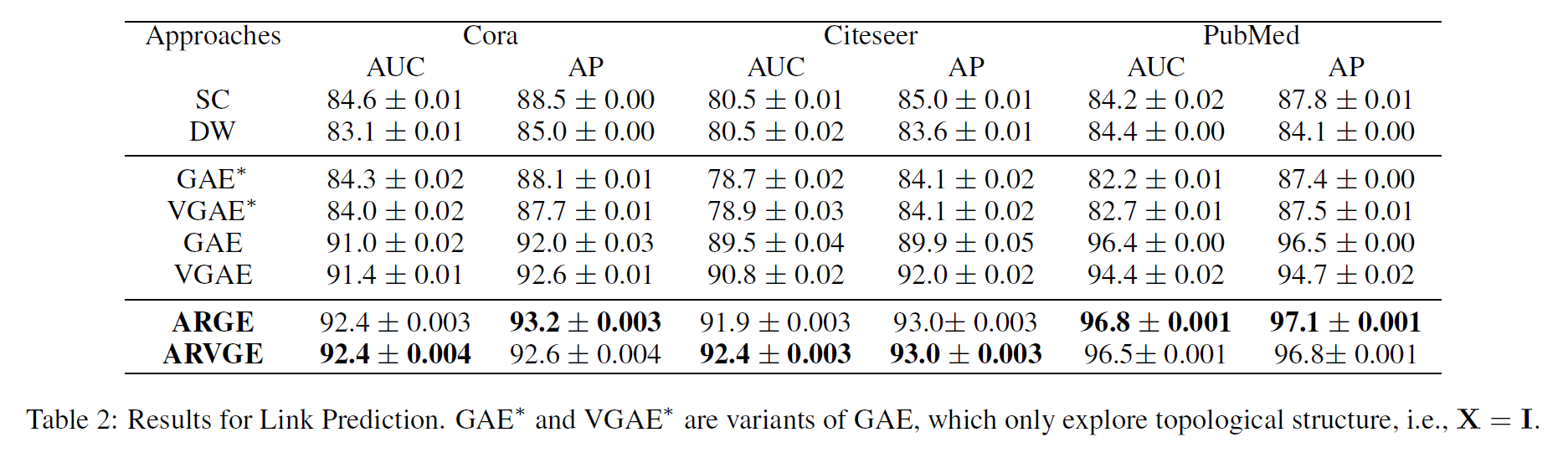
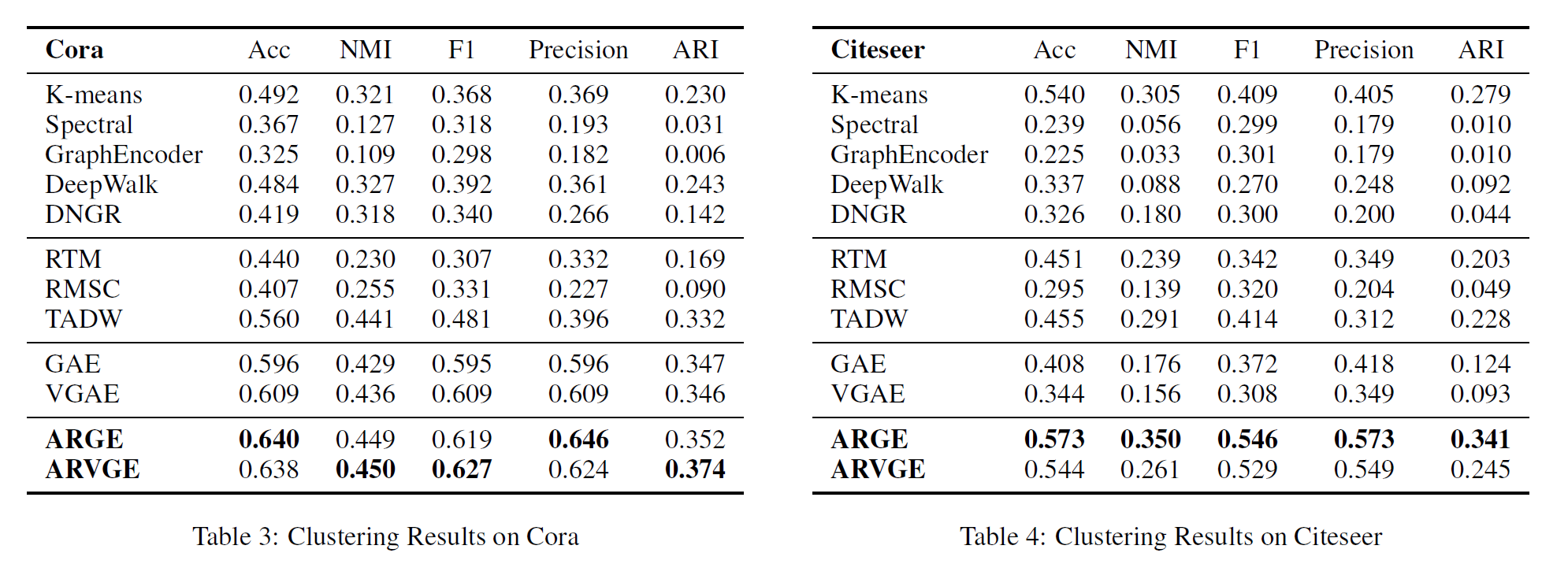
image-20210731203451866 image-20210731203520677

可以看到，节点聚类任务上，ARGE还是明显优于GAE的。

3 Attributed Graph Clustering: A Deep Attentional Embedding Approach（DAEGC）

本文是一个 t-order 模型，即原本的 \(GCN\) 只考虑了一阶邻域，而本方法考虑了 \(t\) 阶邻域。与此相同的还有与本模型同时提出的 \(AGC\) 模型。二者的区别在于 \(DAEGC\) 为 $t-order $ 注意力模型，而 \(AGC\) 为 \(t-order\) 卷积模型

3.1 模型

首先对图的邻接矩阵 \(A\) 进行转移获取 \(t-order\) 邻接矩阵：

\[A = \frac{A + A^2 + A^3 + ... + A^t}{t} \]

然后 encoder 就是一个简单的 \(GAT\) 模型；decoder 的 loss 由结构和特征两部分组成，结构部分与 \(GAE\) 相同，都是 $\hat{A}_{ij} = sigmoid(z_i^T z_j) $ 且 \(L_r = \sum_{i=1}^n loss(A_{i,j}, \hat{A}_{i,j})\)；特征部分采用邻域这一思想，在损失函数中引入中心节点 \(u\)，这样就能表示中心节点周围对于 \(u\) 的距离，使得 \(P\) 的分布尽量接近 \(Q\) 的分布，即上调 \(P\) ，下调 \(Q\) 。

image-20210731210511232

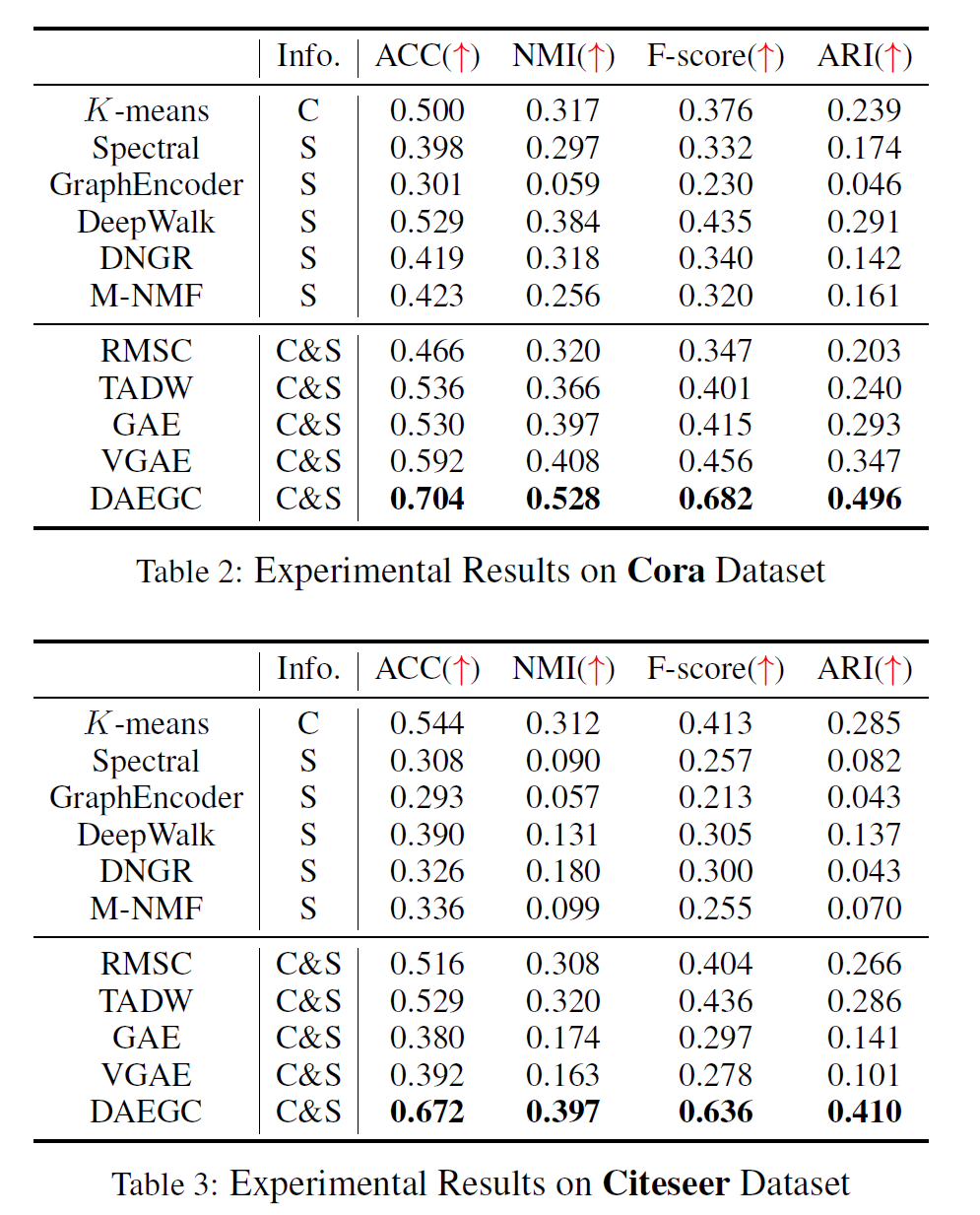
3.2 实验结果

\(DAEGC\) 效果比 \(GAE\) 好很多

image-20210731210609497

4 Graph Attention Auto-Encoders（GATE）

这个之前写过一个博客

https://www.cnblogs.com/popodynasty/p/15064675.html

5 Graph embedding clustering: Graph attention auto-encoder with cluster-specificity distribution(GEC-CSD)

这是一个最近提出的图深度聚类的 SOTA 方法。本篇论文提出的模型将节点表示学习（nodes representations learning）和聚类（clustering）统一到一个框架中，并提出一个新的深度图注意力自编码器（deep graph attention auto-encoder）来做节点聚类，从而利用自注意力机制（self-attention mechanism）和节点属性重构（node attributes reconstruction）来表示节点。此外，该模型还通过\(L_1,L_2\) 范数来约束节点分布。

5.1 迄今提出的图卷积自编码器聚类的局限

  1. 他们忽略了集群特异性分布

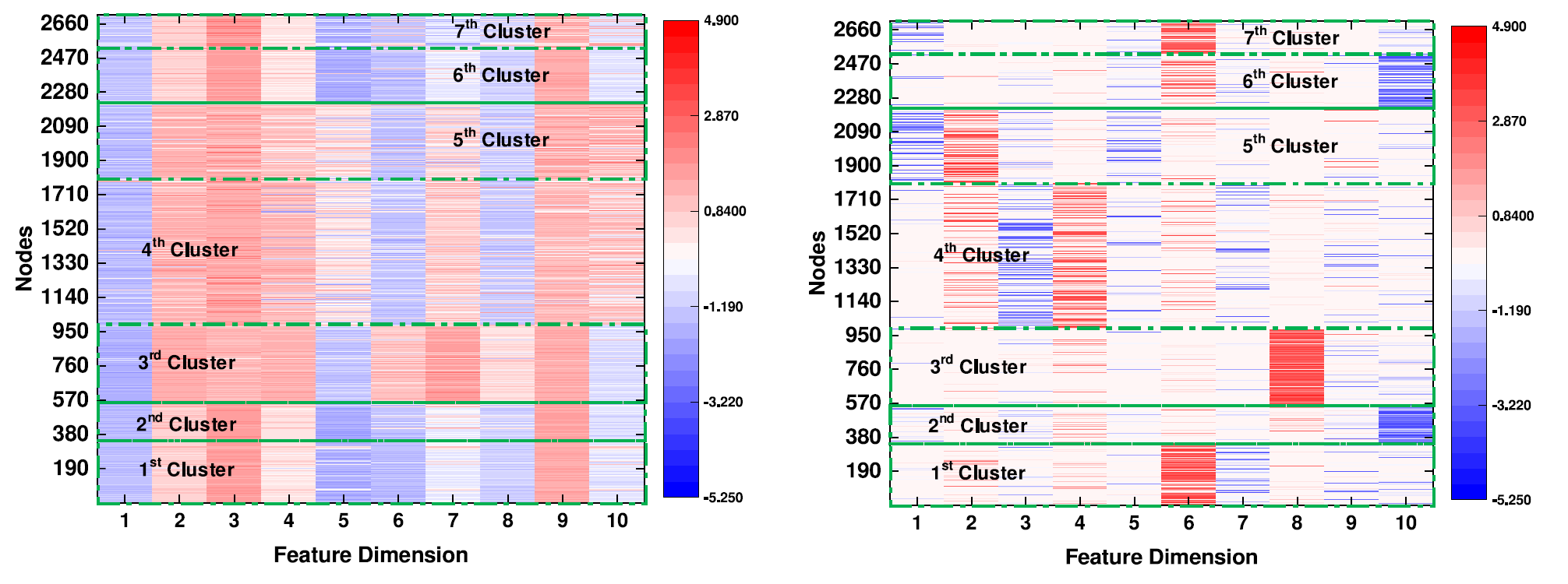
    image-20210801165558079

    上图为 Cora 数据集上的集群特异性分布示意图。

    • 图1中，当没有 CSD 约束时，节点的特征分布在近 10 个维度上，而且它们非常凌乱。即使在多数维度上，节点的特征也非常相似，这可能会使算法将它们全部聚类为同一类。

    • 图2中，节点的特征在 CSD 约束下更具辨别力。例如，属于第一个集群的样本的特征主要集中分布在第6维和第7维。因此，CSD 约束有助于算法划分样本。

  2. 无法同时重构节点属性和图结构，导致 embedding 不够良好

  3. embedding 和 clustering 分别独立进行，因此网络无法通过端到端的方式训练节点集群方式，这限制了它的性能

5.2 主要贡献

  1. 我们提出了一种新颖的基于图注意力自编码器的聚类模型，它加入了节点表示学习和聚类，形成一个统一的框架。 因此，学习到的节点表示不仅可以很好地编码数据信息，还可以很好地编码表征集群结构。
  2. 我们发现 \(L_1,L_2\) 范数在表征图结构数据的维度 CSD 空间，然后将其应用于学习节点表示，这很好地表征了集群结构，因此提高聚类结果。
  3. 聚类时考虑了节点属性重构和节点邻居信息，这有更好地进行图 embedding 。

5.3 相关工作的局限

  1. \(GAE, ARGAE:\) 只对图结构信息进行重构
  2. \(GATE:\) 重构了图节点信息和图结构信息，但只做到了 embedding 这一步，还需要后处理操作以得到聚类标签
  3. \(DAEGC:\) 得到 embedding 并进行了聚类工作，但解码器部分只是简单地进行了一个 \(sigmoid(Z^TZ)\) 计算相似度，即解码器无法学习

无论如何，之前的方法都没考虑 CSD 约束。

5.4 模型

图为 \(GEC-CSD\) 的整体架构：

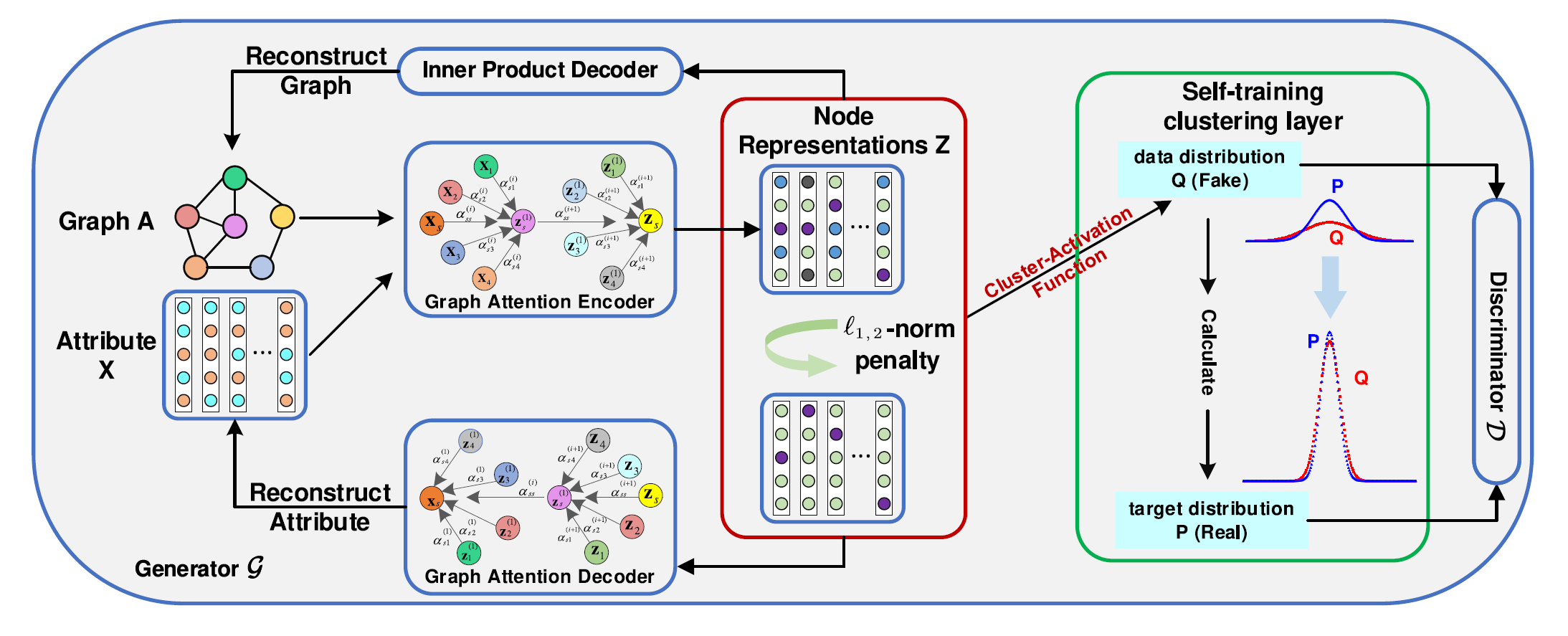
image-20210801184714049

该模型包含两部分：

  • 生成器 \(G\)：

    事实上生成器 \(G\) 就是在之前学到的 \(GATE\) 的基础上，加上了 \(L_{1,2}\) 范式约束。

    • encoder 输入 \(A, X\) ，通过两层非线性的图自注意力编码器，得到潜变量 embedding 矩阵 \(Z\)。

      为了使潜变量 embedding \(Z\) 更具有意义，我们强制 \(Z\) 的实际分布 \(Q\) 尽可能近似一个目标分布 \(P\)。根据 \(t-SNE\) 的思想，如果分布 \(P\) 和分布 \(Q\) 相似，则两个空间的数据也应该近似。因此如果对 \(Z\) 进行聚类得到的簇 \(\mu_t\) 不够理想，那么 \(P,Q\) 就会有较大的差距。

    • decoder 分为两部分，一部分采用内积重建图结构 \(A\)， 另一部分采用两层非线性的图自注意力解码器，重建图节点信息 \(X\)。之前提到 decoder 是部分可学习的，此处可以看出 Inner Product Decoder 不可学习， Graph Attention Decoder 可学习。

    重构损失：

    \[L_R = \frac{1}{N}\sum_{S=1}^N[||x_S-\hat{x}_S]||^2_2 - \epsilon_r \sum_{j \in N_S} \phi (-z_S^Tz_j) \]

    \(L_{1,2}\) 范式惩罚（使得 embedding \(Z\) 的实际分布 \(Q\) 近似目标分布\(P\)）：

    为了使得 embedding 能够更好的用于聚类任务，我们需要对 embedding 的分布进行约束，这是简单的 K-Means 所无法完成的。因此，本文提出了一种优化的聚类方法：定义一个簇类中心矩阵 \(\mu \in \R^{C\times F}\)，它是可训练的。\(\mu\) 第一次被初始化为 \(X\) 的 K-Means 结果。然后本文提出了一个方法来训练 \(\mu\)：

    为了表征节点 embedding 向量 \(z_i\) 与簇类中心 \(\mu_t\) 的关系，本文提出了一个独特的激活函数 \(A(·,·)\) 如下：

    \[A(z_s,\mu_t) =\frac{(1+||z_s-\mu_t||^2)^{-1}}{\sum_{t'}(1+||z_s-\mu_{t'}||^2)^{-1}} \]

    这个激活函数实际上是一个归一化的过程。

    利用这个激活函数，我们可以求得数据的真实分布矩阵 \(Q \in \R^{N\times C}\)，\(q_{st} = A(z_s,\mu_t)\) 。

    接下来，借助 t-SNE 算法的思想，我们可以利用 \(Q\) 来计算一个目标分布 \(P\)，即将 \(Q\) 映射到 \(P\)。我们希望目标分布 \(P\) 具有以下属性：

    （1）它可以进一步强调更多高置信度分配的节点（2）它可以加强预测（3）它可以防止大集群扭曲节点的潜在表示。 最终 \(P\) 的计算公式被定义如下：

    \[p_{st} = \frac{q_{st}^2/\sum_s q_{st}}{\sum_{t'}q_{st'}^2/\sum_sq_{st'}} \]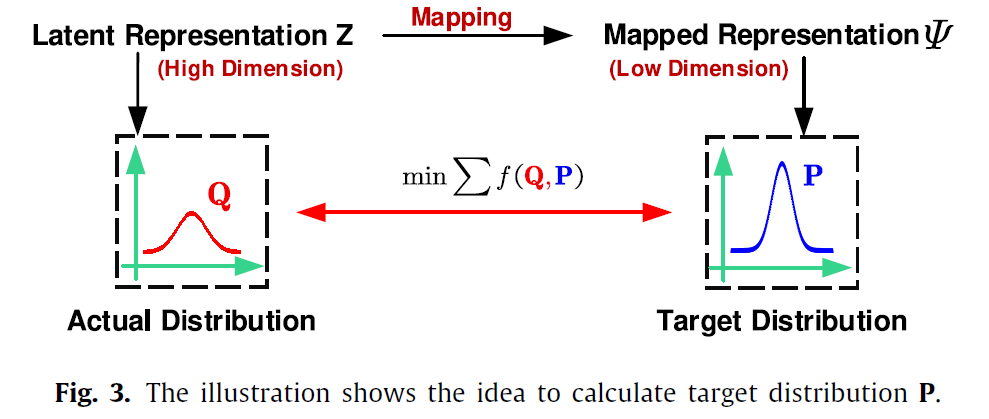

    image-20210801185944844

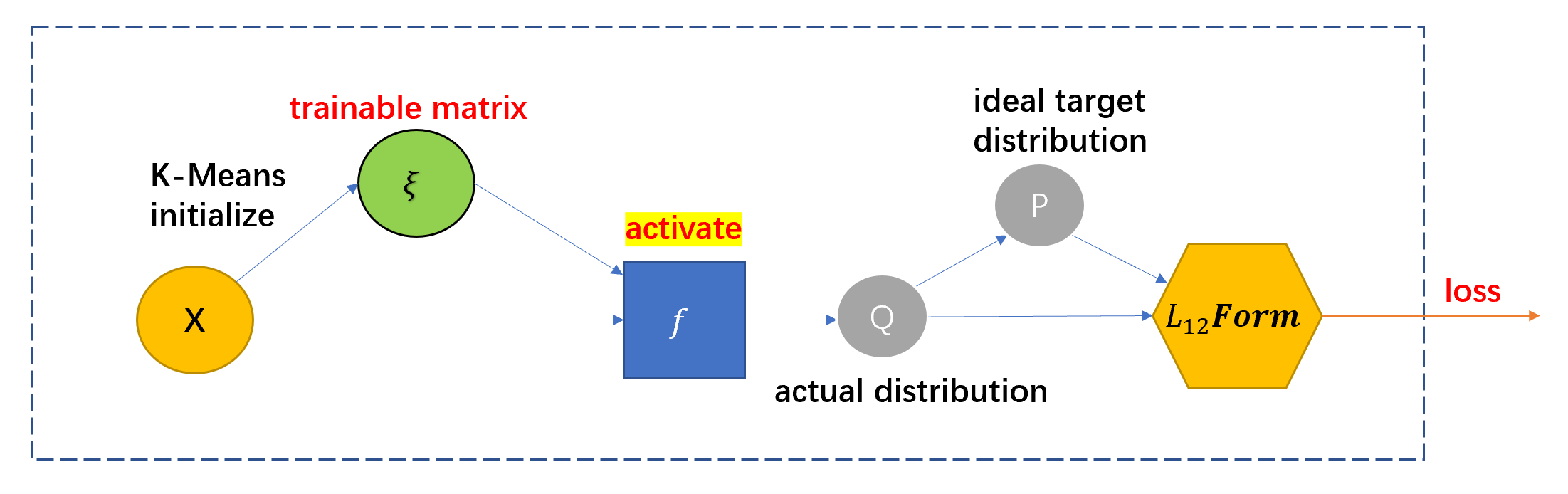
    然后我们期望当前分布与目标分布尽可能接近，一种方法是使用 \(KLD\) ，本文采用的是 \(L_{1-2}\) 范式：

    \[L_C = \sum f(Q,P) = \epsilon_c ||Q-P||^2_F \]

    最后，本文加了一个小 trick ，引入 CSD 损失，一定程度上进一步提升了模型效果

    CSD 损失（使聚类满足集群特异性分布）：

    \[L_{CSD} = \beta||Z||^2_{1,2}=\beta\sum_{S=1}^N||Z_S||^2_1 \]

  • 判别器 \(D:\)

    判别器用于判断当前数据来自目标分布 \(P\)（true）还是 \(G\) 产生的实际分布 \(Q\) （false）

最终模型的聚类结果由 self-training clustering layer 的 \(Q\) 矩阵对各行求最大值索引得到。

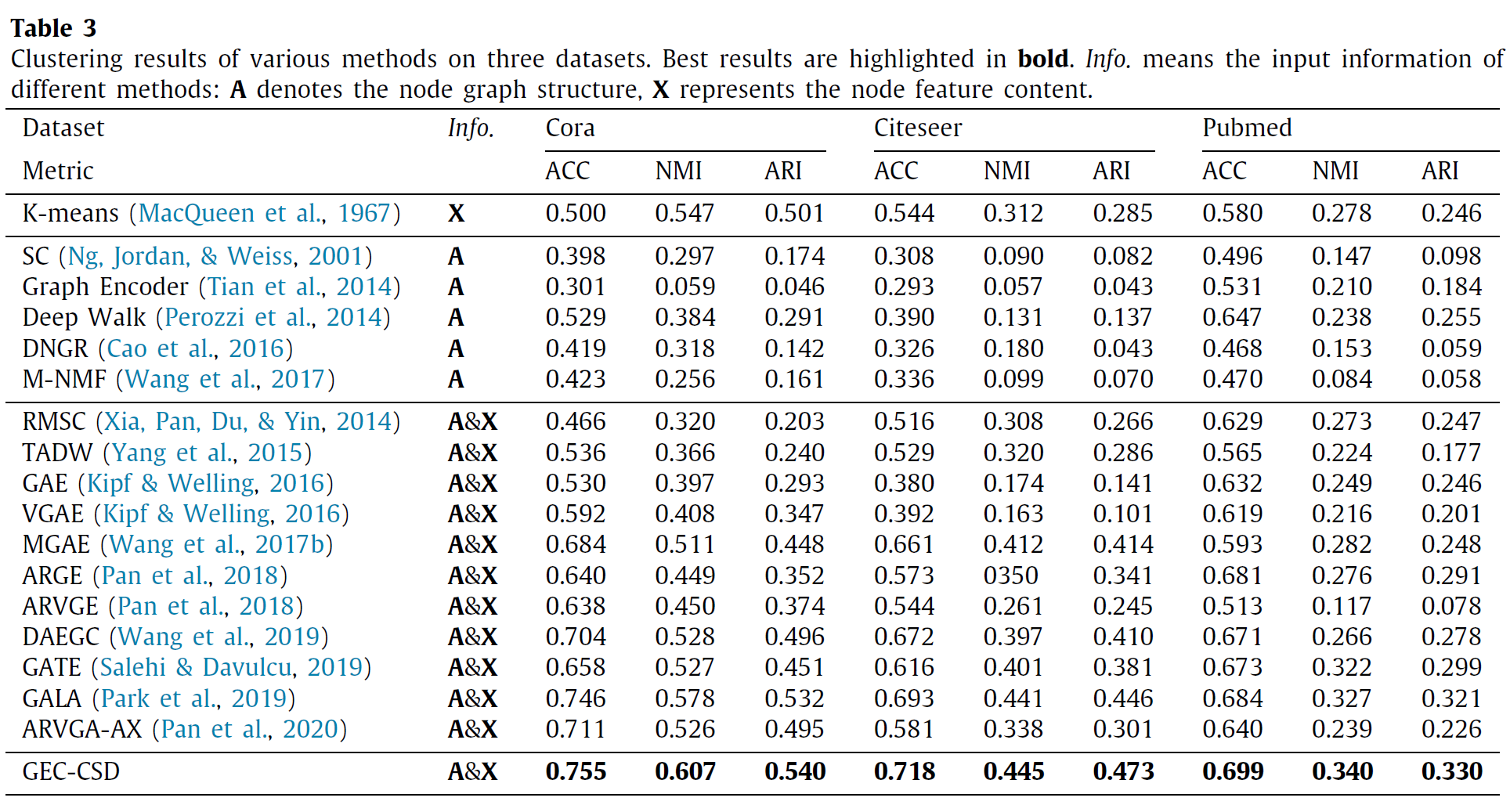
5.5 实验结果

\(SOTA\) 方法

image-20210801193525760

6 Self-supervised graph convolutional clustering by preserving latent distribution（SGCPD）

本文与上一篇 GEC-CSD 同为西交的工作。性能上本文更优。本文提出的框架 SGCPD 主要分为四个模块：

  • Graph Attention Auto-Encoder
  • Distribution Preserving Module
  • Node Clustering Network
  • Self-Supervision Network

整个模型框架图如下：

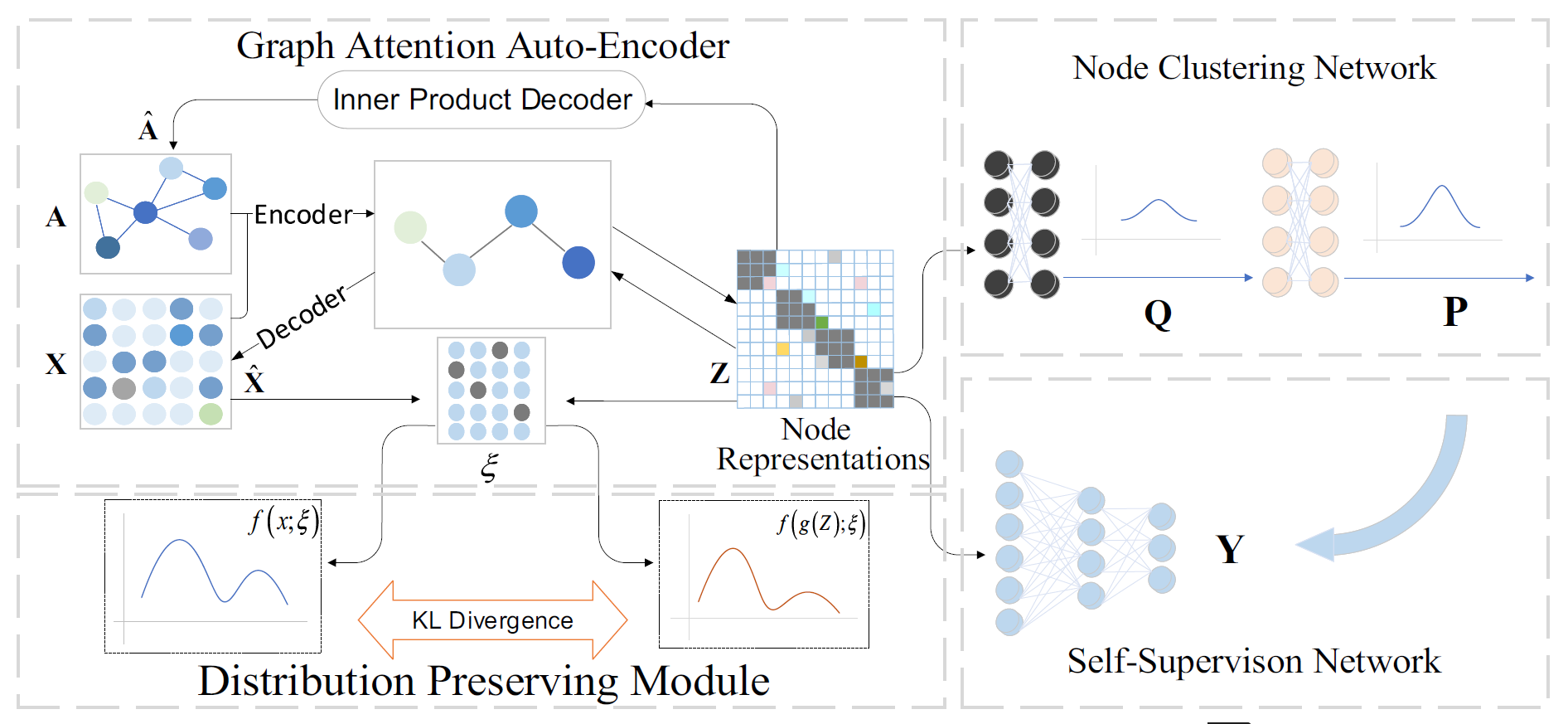
image-20210808201703472

6.1 Graph Attention Auto-Encoder

这里就是简单的两层 GATE 框架，输入 \(X\) 和 \(A\) ，Graph Attention Encoder 学习得到 embedding 矩阵 \(Z\)，Graph Attention Decoder 对 \(Z\) 进行解码输出 \(\hat{X}\) 重构 \(X\)，Inner Product Decoder 对 \(Z\) 进行阶码（简单的内积）输出 \(\hat{A}\) 重构 \(A\)。

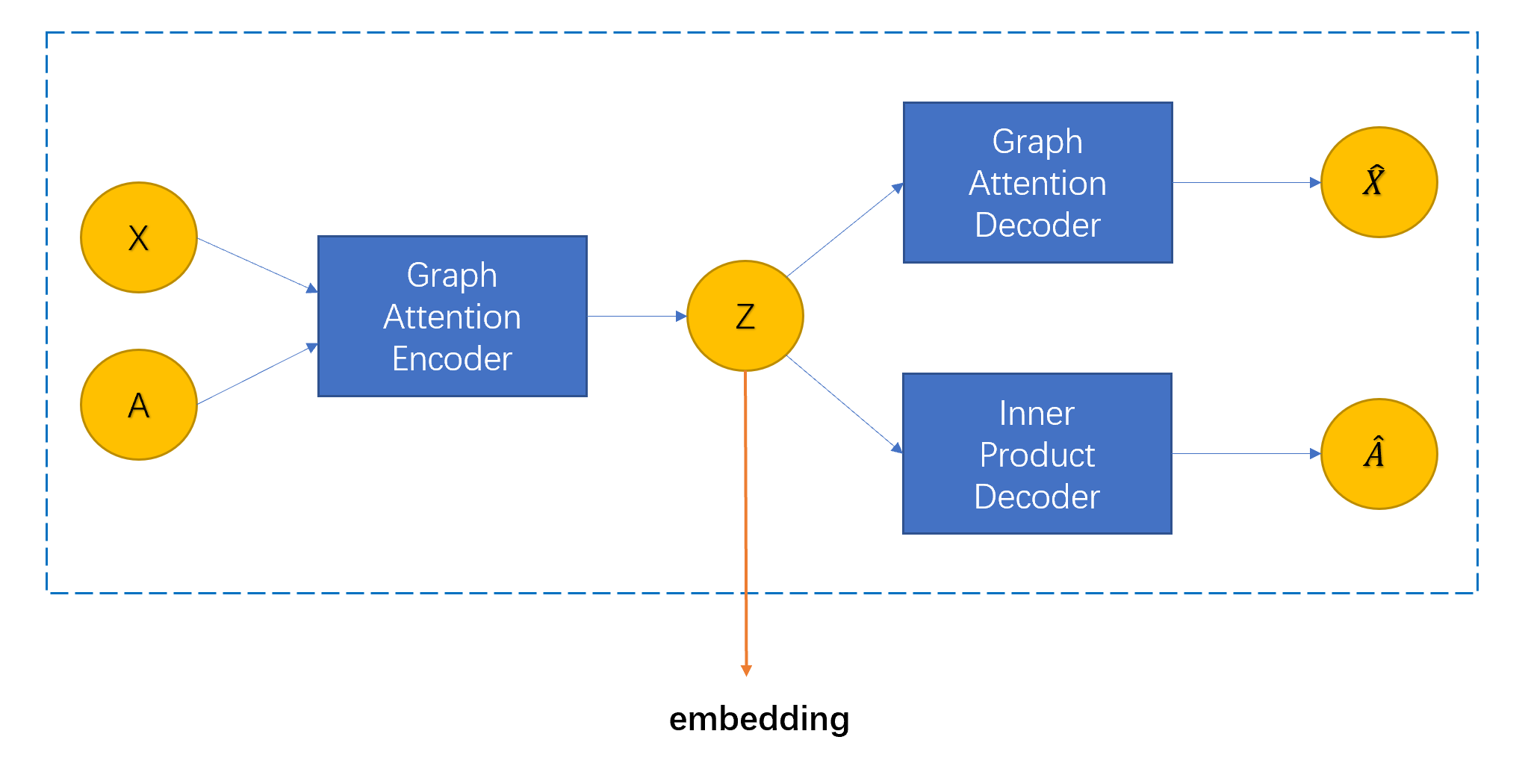
image-20210808201138449

该模块损失表示如下：

\[L_{R_c} = \sum_{i=1}^N ||x_i-\hat{x}_i||^2_2\\ L_{R_a} = \sum_{j\in \N_i} \phi(z_i^Tz_j) \\ L_R = \frac{1}{N}\sum_{i=1}^N[||x_i-\hat{x}_i||^2_2 + \eta_r \sum_{j \in \N_i}\phi(z_i^Tz_j)] \]

6.2 Distribution Preserving Module

设计这一模块的主要目的是使得 embedding 矩阵 \(Z\) 与原本的节点特征矩阵 \(X\) 保持相同的分布。

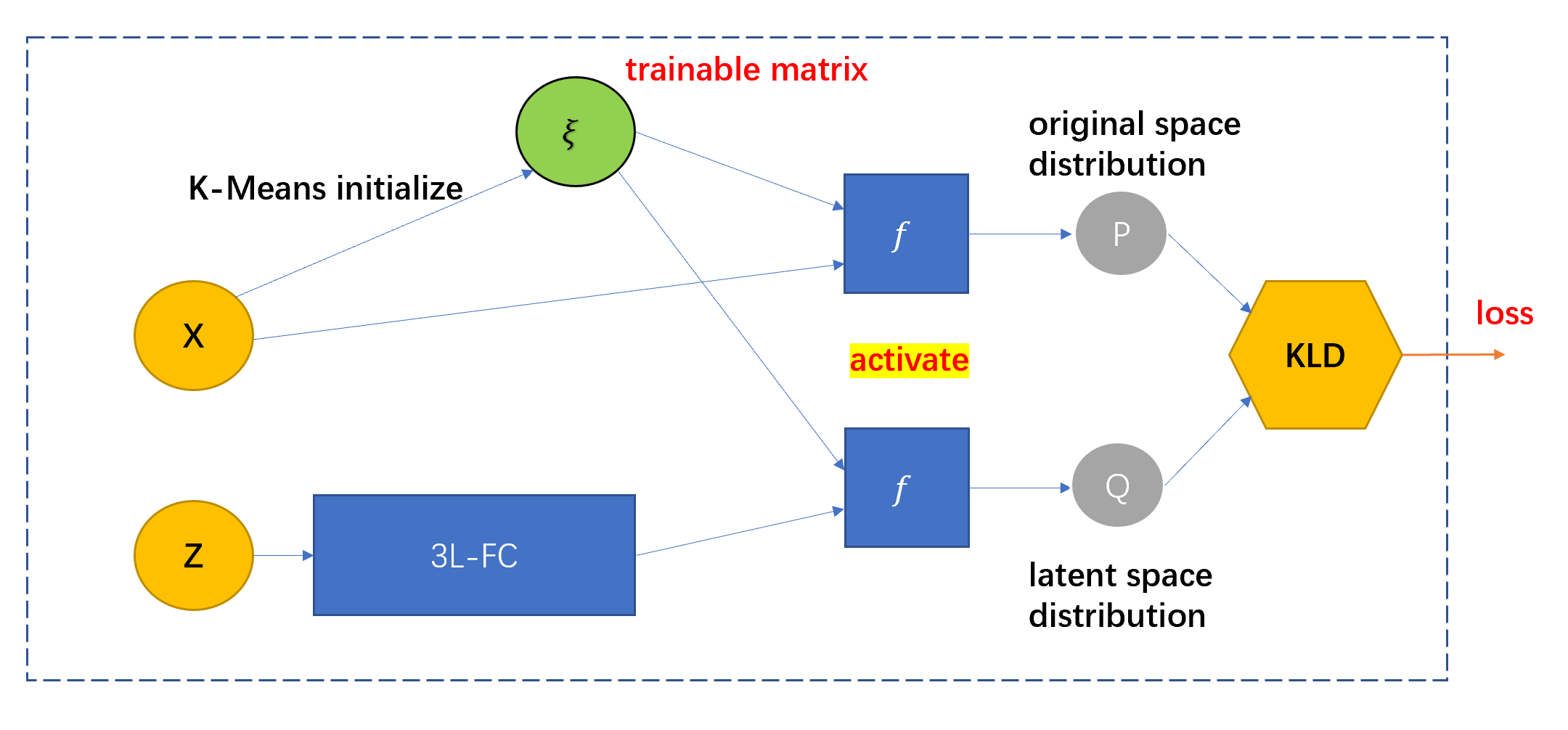
image-20210808223304152

该模块进行的工作如下：

  • 首先定义一个可训练的簇类中心矩阵 \(\xi \in \R^{K\times F}\)。 对节点特征矩阵 \(X \in \R^{N\times F}\) 进行 K-Means 聚类，得到的结果用于初始化 \(\xi\) 。

  • 将 Graph Attention Auto-Encoder 模块得到的 embedding 矩阵 \(Z \in \R^{N \times d}\) 经过一个三层全连接层，线性变换到 \(\R^{N \times F}\)，记作 \(g(Z)\)

  • 将 \(X\) 和 \(g(Z)\) 分别与 \(\xi\) 共同传入一个激活函数函数 \(f(·,·)\) ，得到两个目标分布 \(f(X;\xi)\) 和实际分布 \(f(g(Z);\xi)\)

    这个激活函数 \(f\) 与上一篇论文 GEC-CSD 中提出的激活函数相同，都反映了节点分配到簇类中心的概率。

    \[f(z_s,\mu_t) =\frac{(1+||z_s-\mu_t||^2)^{-1}}{\sum_{t'}(1+||z_s-\mu_{t'}||^2)^{-1}} \]

  • 求上述两个分布的 KLD ，作为该模块的损失，即：

    \[L_D = \sum_{i=1}^N f(X;\xi) \log \frac{f(X;\xi)}{f(g(Z); \xi)} \]

6.3 Node Clustering Network

这一模块 GEC-CSD 的 self-training clustering layer 模块完全一致，作用是约束 embedding 的分布满足 t 分布，以获得一系列良好的特性，这里不再赘述。

image-20210809000500757

最终整个框架的聚类结果由 Node Clustering Network 模块中的 真实分布 \(Q\) 矩阵对各行求最大值索引得到。

6.4 Self-Supervision Network

这一部分是将各个节点的 embedding \(z_i\) 作为 input ，将 Node Clustering Network 中的目标分布 \(p_i\) 作为 label，采用三层全连接网络进行自监督学习的模块。最终该模块的 loss 加入到整个模型的 loss 中，强制 Graph Attention Auto-Encoder 模块学习 \(P\) 分布，进一步使得 embedding 接近目标分布 \(P\) ，从而提高了 embedding 的质量。

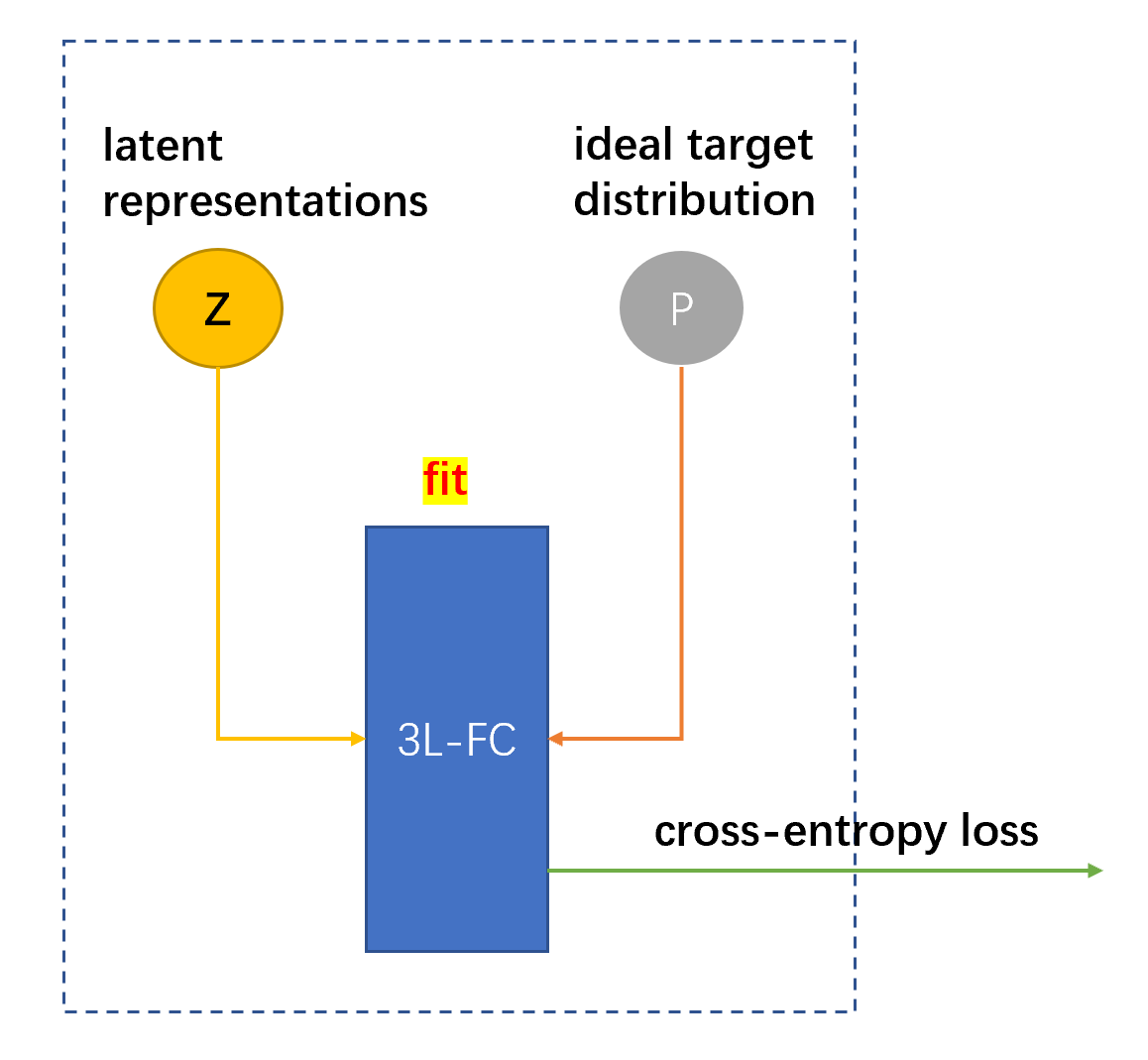
image-20210809001348949

6.5 整个框架

整个框架的 loss 合并了各个模块的 loss，即：

\[\varphi = \varphi_R \text{(reconstruction loss)} + \lambda_1 \varphi_D \text{(distribution loss)} + \lambda_2 \varphi_C \text{(node clustring loss)} + \lambda_3 \varphi_S \text{(self-supervision loss)} \]

模型最终的聚类结果直接由 Node Clustering Network 模块中的真实分布矩阵 \(Q\) 对各行求最大值索引得到。

6.6 实验结果

image-20210809002331165

posted @ 2021-08-01 20:07  popozyl  阅读(1597)  评论(4)  编辑  收藏  举报