线段树 - dfs序映射至线段树解决区间染色问题 / 时间戳 - HDU 3974 - Assign the task
线段树 - dfs序映射至线段树解决区间染色问题 / 时间戳 - HDU 3974 - Assign the task
解法1: 模拟多叉树(数据极端的情况下,复杂度极大)
1. 分配任务操作
对于每一个分配任务操作,我们可以记录分配的任务编号以及分配任务时间.
由于可能存在大量的任务分配操作,我们借鉴线段树的思想,使用lazy数组来延迟更新.此外,我们还需要记录分配任务时间顺序,这是因为,如果不记录分配任务的时间顺序,在后面更新lazy标记的时候,可能存在旧的任务覆盖新的任务的情况.
int taskOf[N];
int isLazy[N];
void assign(int id,int task,int time){
taskOf[id] = task;
isLazy[id] = time;
}
2. 查询操作
我们查询某一个员工的任务,首先需要将它的所有祖先的lazy标记下放.我们应该从树根下放lazy标记,然后一步步得到当前员工结点的任务.
这么做就会遇到我们刚刚所讲的问题:旧的任务覆盖新的任务的情况. 试想这样一种情况, A是B的上司,B是C的上司,我们先给A分配任务1,再给B分配任务2; 此时, lazy标记都没有下放; 然后,我们查询C当前的任务,那么我们会先下放A的lazy标记给B,此时B的lazy标记被覆盖了,然后B的lazy标记下放给C,得到C的任务是1.这显然是错误的.因此,我们对于lazy下放的操作需加一个前置条件: 父结点的lazy时间戳要大于子结点的lazy时间戳才可下放.
void query(int id){
if(parentOf[id]){
query(parentOf[id]);
}
if(Islazy[id]){
for(vector<int> :: iterator it = childOf[id].begin(); it != childOf[id].end(); it++){
if(Islazy[*it] < Islazy[id]){
// 如果根结点具备更新的时间戳,那么子结点的时间戳也被更新; 如果子结点根本不存在时间戳(没有更新点,是0),那么也会直接更新
taskOf[*it] = taskOf[id];
Islazy[*it] = Islazy[id];
}
}
Islazy[id] = 0;
}
}
3.完整代码
#include <cstdio>
#include <vector>
#include <cstdlib>
using namespace std;
#define N 50000+50
vector<int> childOf[N];
int parentOf[N];
int taskOf[N];
int Islazy[N];
void assign(int id,int task,int time){
taskOf[id] = task;
Islazy[id] = time;
}
void query(int id){
if(parentOf[id]){
query(parentOf[id]);
}
if(Islazy[id]){
for(vector<int> :: iterator it = childOf[id].begin(); it != childOf[id].end(); it++){
if(Islazy[*it] < Islazy[id]){
// 如果根结点具备更新的时间戳,那么子结点的时间戳也被更新; 如果子结点根本不存在时间戳(没有更新点,是0),那么也会直接更新
taskOf[*it] = taskOf[id];
Islazy[*it] = Islazy[id];
}
}
Islazy[id] = 0;
}
}
int main(){
int T; // 10
scanf("%d",&T);
for(int g = 1; g <= T; g++){
printf("Case #%d:\n",g);
int n,m; // 5e5
int a,b;
char cmd[5];
scanf("%d",&n);
for(int i = 1; i <= n; i++){
childOf[i].clear();
taskOf[i] = -1;
Islazy[i] = 0;
parentOf[i] = 0;
}
for(int i = 1; i < n; i++){
scanf("%d%d",&a,&b);
childOf[b].push_back(a);
parentOf[a] = b;
}
scanf("%d",&m);
for(int i = 1; i <= m; i++){
scanf("%s",cmd);
if(cmd[0] == 'T'){
scanf("%d%d",&a,&b);
// assign task b to employee a
assign(a,b,i); // i 时间戳
}else{
scanf("%d",&a);
// query task of employee a
query(a);
printf("%d\n",taskOf[a]);
}
}
}
system("pause");
return 0;
}
然而,这种算法当整棵树为一条链状时会达到最坏复杂度O(T*m*n),需要考虑更加稳定的解法*
解法2: dfs序映射至线段树
我们可以记录一棵树的dfs序将其映射到区间上,例如一棵树
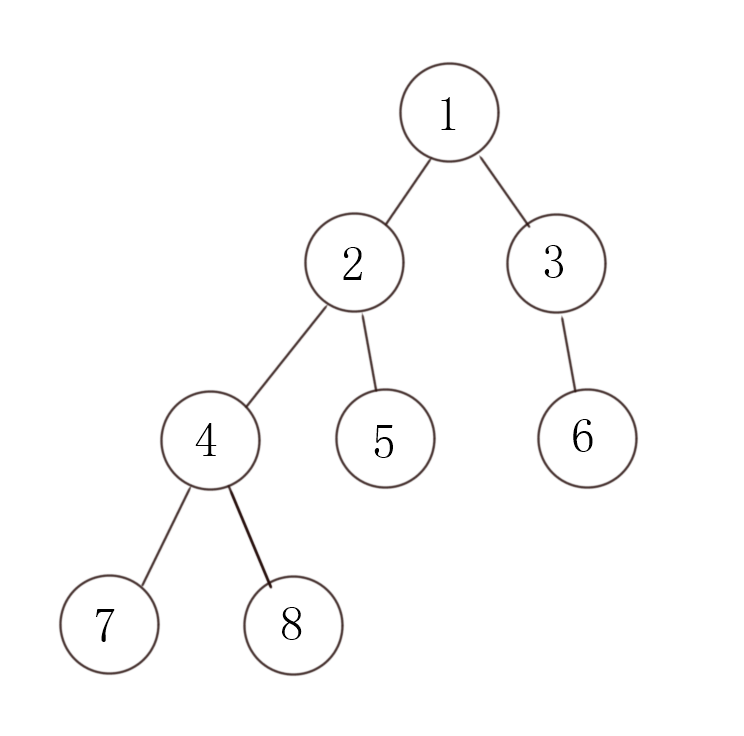
我们通过dfs来访问各个结点的顺序是
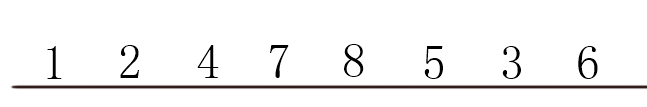
如果再把重新回到该结点的状态也标注出来,就是:
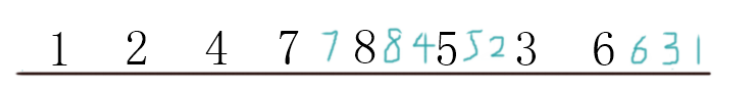
可以看出,通过标注dfs序,我们将树的父子关系映射成了连续的区间关系,
即:
- 1号结点影响的数字为$[1,2,4,7,8,5,3,6] \(, 即区间\)[1,8]$
- 2号结点影响的数字为\([2,4,7,8,5]\),即区间\([2,6]\)
- 3号结点影响的数字为\([3,6]\),即区间\([7,8]\)
- 4号结点影响的数字为\([4,7,8]\),即区间\([3,5]\)
- 5号结点影响的数字为\([5,5]\),即区间\([6,6]\)
- 6号结点影响的数字为\([6,6]\),即区间\([7,7]\)
- 7号结点影响的数字为\([7,7]\),即区间\([4,4]\)
- 8号结点影响的数字为\([8,8]\),即区间\([5,5]\)
此时问题被转化成了:对于区间[1,8],修改一段子区间的值,然后查询某个孤立点的值
- 对于一个修改操作:
题目给定一个员工和分配的任务,我们通过记录dfs序来转变成
修改区间[update_left,update_right]为value
- 对于一个查询操作:
题目给定一个员工的编号,我们查询的是区间的某个孤立点的值
如查询三号员工的任务,我们记录的三号员工dfs序是第7位,那么问题转变为求区间[7,7]的值
剩下的操作就是线段树的模板了,记得还是要加时间戳,因为它是一个染色问题,具有先后顺序.
#include <cstdio>
#include <vector>
#include <cstdlib>
using namespace std;
#define N 50000+5
int mapPtr = 0;
int leftMap[N];
int rightMap[N];
int taskOf[N<<2];
int timeOf[N<<2];
int isRoot[N];
vector<int> childOf[N];
void Map(int root){
leftMap[root] = ++mapPtr;
for(vector<int> :: iterator it = childOf[root].begin(); it != childOf[root].end(); it++){
Map(*it);
}
rightMap[root] = mapPtr;
}
void update(int left,int right,int root,int update_left,int update_right,int newTask,int time){ // [update_left,update_right] -> newTask
if(update_left <= left && update_right >= right){
if(time > timeOf[root]){
taskOf[root] = newTask;
timeOf[root] = time;
}
}else{
int mid = (left+right)>>1;
if(update_left <= mid){
update(left,mid,root<<1,update_left,update_right,newTask,time);
}
if(update_right > mid){
update(mid+1,right,root<<1|1,update_left,update_right,newTask,time);
}
}
}
int query(int left,int right,int root,int querypos){
if(left == querypos && right == querypos){
return taskOf[root];
}else{
int mid = (left+right)>>1;
if(querypos <= mid){
if(timeOf[root] > timeOf[root<<1]){
taskOf[root<<1] = taskOf[root];
timeOf[root<<1] = timeOf[root];
}
return query(left,mid,root<<1,querypos);
}else{
if(timeOf[root] > timeOf[root<<1|1]){
taskOf[root<<1|1] = taskOf[root];
timeOf[root<<1|1] = timeOf[root];
}
return query(mid+1,right,root<<1|1,querypos);
}
}
}
int main(){
int T;
scanf("%d",&T);
for(int g = 1; g <= T; g++){
printf("Case #%d:\n",g);
int n;
int a,b;
scanf("%d",&n);
for(int i = 1; i <= n; i++){
childOf[i].clear();
isRoot[i] = 1;
}
int temp = n<<2;
for(int i = 1; i <= temp; i++){
taskOf[i] = -1;
timeOf[i] = 0;
}
mapPtr = 0;
int rootId = 0;
for(int i = 1; i < n; i++){
scanf("%d%d",&a,&b);
childOf[b].push_back(a);
isRoot[a] = 0;
}
for(int i = 1; i <= n; i++){
if(isRoot[i]){
rootId = i;
break;
}
}
Map(rootId);
int m;
char cmd[5];
scanf("%d",&m);
for(int i = 1; i <= m; i++){
scanf("%s",cmd);
if(cmd[0] == 'T'){
scanf("%d%d",&a,&b);
// a->b
update(1,mapPtr,1,leftMap[a],rightMap[a],b,i);
}else{
scanf("%d",&a);
printf("%d\n",query(1,n,1,leftMap[a]));
}
}
}
system("pause");
return 0;
}
简单分析一下这个算法的时间复杂度:
dfs序映射区间: O(n)
区间修改,单点查询: O(logn)
总程序复杂度: O(T*(n+m*logn))


