最近公共祖先（LCA）
什么是LCA
最近公共祖先是相对于两个节点来说的，顾名思义，最近公共祖先即为两个节点公共的最近的祖先。
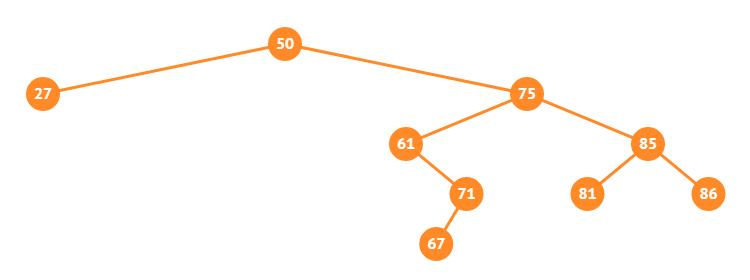
如上图，\(86\) 和 \(67\) 的 \(LCA\) 是 \(75\)，\(67\) 和 \(27\) 的 \(LCA\) 是 \(50\)。
怎么求LCA
倍增法
我们先想想暴力怎么做：从这两个节点开始，一步一步往上跳，直到跳到了一起，那么就是 \(LCA\) 了。
那我们该怎么优化暴力呢？我们可以一次跳多个节点呀！如果我们在每一个节点上，都先预处理出 \(log(n)\) 个节点信息，分别表示向上走 \(1\) 步，\(2\) 步，\(4\) 步，\(8\) 步，\(\dots\)，\(2^k\) 步所到达的节点。这样我们只需要 \(log(n)\) 步就可以走到根节点。
然后仍然套用之前暴力的方法向上走即可。
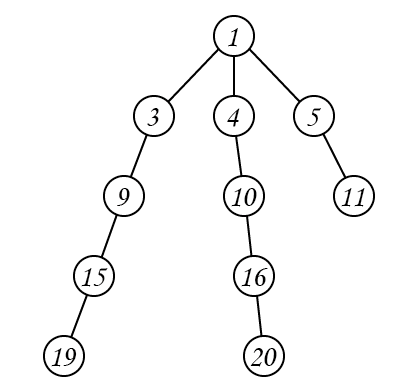
上面树的节点信息如下：
| 节点 | 节点信息 |
|---|---|
| \(19\) | 跳 \(1\) 步：\(15\)；跳 \(2\) 步：\(9\)；跳 \(4\) 步：\(1\) |
| \(20\) | 跳 \(1\) 步：\(16\)；跳 \(2\) 步：\(10\)；跳 \(4\) 步：\(1\) |
| \(16\) | 跳 \(1\) 步：\(10\)；跳 \(2\) 步：\(4\) |
| \(10\) | 跳 \(1\) 步：\(4\)；跳 \(2\) 步：\(1\) |
如何记录这些节点信息呢？
初始我们只知道向上走 \(1\) 步的信息。
然后根据走 \(1\) 步的信息，推出走 \(2\) 的信息。
再根据走 \(2\) 步的信息，推出走 \(4\) 步的信息。
\(\dots\)
很明显我们通过递推就可以求出来了。
我们用数组 \(f[u][k]\) 表示节点 \(u\) 向上走 \(2^k\) 步所走到的点，显然有 \(f[u][0] = u\) 的父亲节点，则我们的递推式则为：
\(f[u][k] = f[f[u][k - 1]][k - 1]\)
for (int k = 1; k <= 20; ++k)
for (int u = 1; u <= n; ++u)
f[u][k] = f[f[u][k - 1]][k - 1];
在求 \(x,y\) 两个节点的 \(LCA\) 时，如果 \(x,y\) 深度不同，则先让深度较大的节点向上跳到另一个节点所在的深度。记 \(dep[u]\) 表示节点 \(u\) 的深度，假设 \(dep[x] > dep[y]\)，那么先让 \(x\) 倍增的向上跳 \(dep[x] - dep[y]\) 步。
int tmp = dep[x] - dep[y];
for (int i = 20; i >= 0; --i)
if (tmp & (1 << i))
x = f[x][i];
当两个节点深度相同时，就同时倍增的向上跳，但是又不能让他们跳过 \(LCA\)。具体来说，我们从大到小枚举 \(k\)，判断 \(x, y\) 同时向上走 \(2 ^ j\) 步是否会相遇，如果不会，则向上跳 \(2 ^ j\) 步。重复这个过程，此时 \(x, y\) 就会跳到 \(LCA\) 的子儿子处，此时再进一步就是 \(LCA\)。
for (int k = 20; k >= 0; --k)
if (f[x][k] != f[y][k])
x = f[x][k], y = f[y][k];
if (x != y) x = f[x][0], y = f[y][0];
// 此时x和y都是LCA
题目：
举个例子：
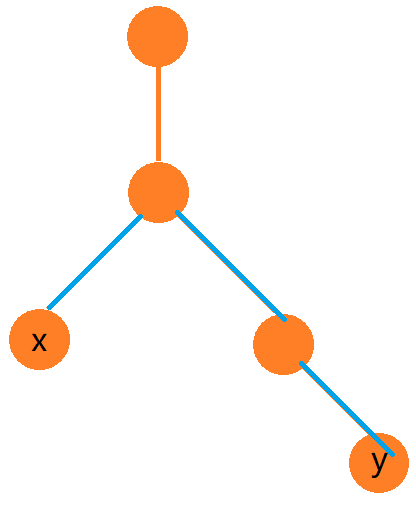
如果我们记录了每个点到根节点的边权和 \(dis_i\)，则从 \(x\) 到 \(y\) 的路径边权和即为
\(dis_i + dis_j - 2 \times dis_{LCA(i, j)}\)
代码：
#include <bits/stdc++.h>
#define N 100010
using namespace std;
int n, m;
int h[N], e[N * 2], w[N * 2], ne[N * 2], idx;
bool vis[N];
int dis[N], dep[N];
int f[N][30], fa[N];
void add(int a, int b, int c) { e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++; }
void dfs(int u, int father) {
fa[u] = father;
for (int i = h[u]; i != -1; i = ne[i]) {
int j = e[i];
if (j != father) {
dep[j] = dep[u] + 1;
dis[j] = dis[u] + w[i];
dfs(j, u);
}
}
}
int lca(int x, int y) {
if (dep[x] < dep[y]) swap(x, y);
int tmp = dep[x] - dep[y];
for (int k = 20; k >= 0; --k)
if (tmp & (1 << k))
x = f[x][k];
for (int k = 20; k >= 0; --k)
if (f[x][k] != f[y][k])
x = f[x][k], y = f[y][k];
if (x != y) x = f[x][0], y = f[y][0];
return x;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
memset(h, -1, sizeof h);
cin >> n >> m;
for (int i = 1; i <= n - 1; ++i) {
int a, b, c;
cin >> a >> b >> c;
add(a, b, c), add(b, a, c);
}
dfs(1, 0);
for (int i = 1; i <= n; ++i) f[i][0] = fa[i];
for (int k = 1; k <= 20; ++k)
for (int u = 1; u <= n; ++u)
f[u][k] = f[f[u][k - 1]][k - 1];
while (m--) {
int x, y;
cin >> x >> y;
cout << dis[x] + dis[y] - 2 * dis[lca(x, y)] << '\n';
}
return 0;
}
Tarjan
用 \(Tarjan\) 算法也是可以求 \(LCA\) 的，但是它是一种离线算法。所谓离线算法，就是说它不会在查询两个节点的 \(LCA\) 时直接给出答案，而是等到所有查询操作都给出后统一进行求解。
相比于倍增法，\(Tarjan\) 的效率很高，时间复杂度最低可以达到 \(O(n + q) \times 并查集的复杂度\)。
由于作者不会按秩合并，所以大家时间如果时间充裕的话并查集用个路径压缩就行了。
我们考虑以下过程：
在对一棵树进行 \(DFS\) 的过程中，对于一对点 \(x\) 和 \(y\)，我们肯定是先遍历到一个，再后遍历到一个。
不妨假设先遍历到 \(x\)，再遍历到 \(y\)。
当我们遍历完 \(x\) 时，我们肯定会回溯到 \(x\) 的祖先节点 \(p\)，然后接着遍历其祖先节点的其它子树，直到遍历到某一个子树里遍历到 \(y\) 了，我们惊喜的发现，\(p\) 就是 \(x\) 和 \(y\) 的最近公共祖先了。
具体来说，\(Tanjan\) 的算法流程如下：
- 维护一个并查集。
- 任选一个节点作为根节点进行 \(DFS\)。
- 当我们遍历到一个点 \(u\) 时，遍历其所有子节点 \(v\)，并将 \(v\) 标记为已访问，接着遍历 \(v\)。
- 合并 \(u\) 和 \(v\) 的并查集，将 \(find(v)\) 作为并查集的子节点连在 \(find(u)\) 的下面（使得深度更浅的节点作为并查集的根）。
- 处理与 \(u\) 节点相关的询问 \(LCA(u, x)\)，如果 \(x\) 已经被访问过，那么 \(LCA(u, x)\) 就是 \(find(x)\)。
伪代码：
tarjan(u) {
for (u -> v) { // 遍历u所有有子节点v
vis[v] = true; // 标记为已访问
tarjan(v)； // 继续向下遍历
marge(u, v); // 合并并查集
}
for (query(u, x)) { // 处理所有与u节点相关的询问
if (vis[x]) ans[(u, x)] = find(x); // 给出答案
}
}
