线段树

例题1：

给定一个正整数数列 \(a_1,a_2,…,a_n\)，每一个数都在 \(0 \sim p-1\) 之间。 可以对这列数进行两种操作：

1. 添加操作：向序列后添加一个数，序列长度变成 \(n+1\)；
2. 询问操作：询问这个序列中最后 \(L\) 个数中最大的数是多少。

程序运行的最开始，整数序列为空。 一共要对整数序列进行 \(m\) 次操作。 写一个程序，读入操作的序列，并输出询问操作的答案。
数据范围

\(1 \le m \le 2 \times 10^5\)
\(1 \le p \le 2 \times 10^9\)
\(0 \le t < p\)

这道题看第一眼：暴力，再看一眼：爆炸（bushi TLE。
这道题目就可以用我们今天要学的线段树来解决。

线段树的思路

线段树是一棵二叉树，它可以在很低的时间复杂度内完成一个序列的单点修改、区间修改、区间查询（最大数，最小数、求和等等）等的操作， \([1, n]\) 线段树支持的所有操作都可以将时间复杂度控制在\(O(log\ n)\)。
线段树俗称段错误树，因调试时经常段错误而得名
它的的思路很好理解， 顾名思义，它就是一个节点为线段的树；假设我们要用线段树维护一个区间 \([1, 10]\) ：

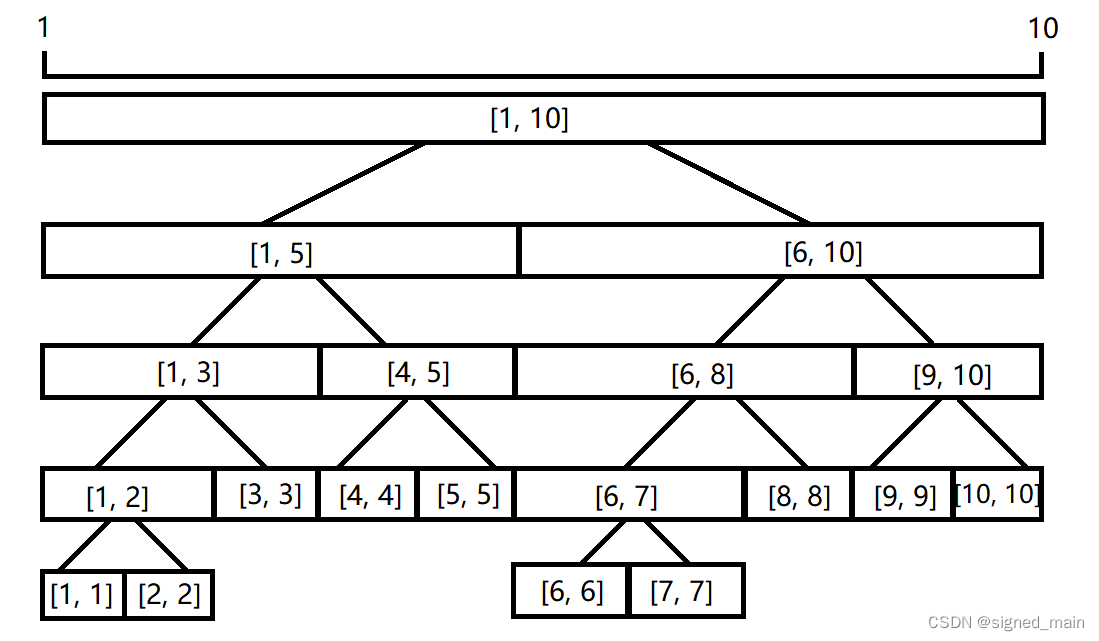
如何存储线段树

我们直接拿一个结构体来存储线段树，每一个节点都是一段区间，拿刚才的例题举例：

struct Node {
    int l, r; // 区间的左端点和右端点
    int v; // 区间[l, r]中的最大值
    // 这里可以存储你要维护的任何信息，例如最大/最小值，区间和等
} tr[N * 4];

一棵线段树的根节点编号为 \(1\) ，设一个不为根节点的节点编号为 \(u\) ，则这个节点的父节点是 \(\lfloor {\frac{u}{2}} \rfloor\) ，它的左儿子编号为 \(2 \times u\) ，右儿子编号为 \(2 \times u + 1\) ；因为一颗线段树最大是一棵满二叉树，N个叶子节点的满二叉树最多有 \(N + N \div 2 + N \div 4 + ... + 2 + 1 = 2N - 1\) 个节点；而最后一层（可以参考上面的 \([1, 10]\) 线段树图）最多还会剩余 \(2N\) 个节点。所以线段树通常需要开 \(4N\) 倍的空间。

如何建立线段树

线段树中如果表示的区间为 \([l, r]\) 且这个节点不为叶子节点（\(l \ne r\)），则我们有一个 \(mid = \lfloor{\frac{l + r}{2}}\rfloor\) , 这个点的左子树即为 \([l, mid]\) ，右子树即为 \([mid + 1, r]\) ，递归建树即可。
代码：

void pushup(int u) { // 由子节点的最大值，来更新父节点的信息
    tr[u].v = max(tr[u * 2].v, tr[u * 2 + 1].v);
}
void build(int u, int l, int r) {
    tr[u] = {l, r};
    if (l == r)
        return;
    int mid = l + r >> 1;
    build(u * 2, l, mid), build(u * 2 + 1, mid + 1, r);
}

如何进行查询

递归查询，直到我们树中结点已经完全包含在我们需要查询的区间中
代码：

int query(int u, int l, int r) {
    if (tr[u].l >= l && tr[u].r <= r)
        return tr[u].v; //  树中节点已经被完全包含在[l, r]中了
    int mid = tr[u].l + tr[u].r >> 1;
    int v = 0;
    if (l <= mid)
        v = query(u * 2, l, r);
    if (r > mid)
        v = max(v, query(u * 2 + 1, l, r));
    return v;
}

如何进行修改

递归寻找，直到我们找到了我们将要修改的叶子节点（只有一个数的区间），进行修改。

void modify(int u, int x, int v) {
    if (tr[u].l == x && tr[u].r == x)
        tr[u].v = v;
    else {
        int mid = tr[u].l + tr[u].r >> 1;
        if (x <= mid)
            modify(u * 2, x, v);
        else
            modify(u * 2 + 1, x, v);
        pushup(u); //	别忘了告诉父节点我们刚刚进行更新的信息
    }
}

例题1完整代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 200010;
int m, p;
struct Node {
    int l, r;
    int v;
} tr[N * 4];
void pushup(int u) { tr[u].v = max(tr[u * 2].v, tr[u * 2 + 1].v); }
void build(int u, int l, int r) {
    tr[u] = {l, r};
    if (l == r)
        return;
    int mid = l + r >> 1;
    build(u * 2, l, mid), build(u * 2 + 1, mid + 1, r);
}
int query(int u, int l, int r) {
    if (tr[u].l >= l && tr[u].r <= r)
        return tr[u].v;
    int mid = tr[u].l + tr[u].r >> 1;
    int v = 0;
    if (l <= mid)
        v = query(u * 2, l, r);
    if (r > mid)
        v = max(v, query(u * 2 + 1, l, r));
    return v;
}
void modify(int u, int x, int v) {
    if (tr[u].l == x && tr[u].r == x)
        tr[u].v = v;
    else {
        int mid = tr[u].l + tr[u].r >> 1;
        if (x <= mid)
            modify(u * 2, x, v);
        else
            modify(u * 2 + 1, x, v);
        pushup(u);
    }
}
int main() {
    int n = 0, last = 0;
    scanf("%d%d", &m, &p);
    build(1, 1, m);
    char op[2];
    int x;
    while (m--) {
        scanf("%s%d", op, &x);
        if (*op == 'Q') {
            last = query(1, n - x + 1, n);
            printf("%d\n", last);
        } else {
            modify(1, n + 1, ((ll)last + x) % p);
            n++;
        }
    }
    return 0;
}

进阶线段树（线段树的懒标记）

例题2：

给定一个长度为 \(N\) 的数列 \(A\)，以及 \(M\) 条指令，每条指令可能是以下两种之一：

1. C l r d，表示把 \(A[l],A[l+1],…,A[r]\) 都加上 \(d\)。
2. Q l r，表示询问数列中第 \(l \sim r\) 个数的和。

对于每个询问，输出一个整数表示答案。
数据范围

\(1 \le N,M \le 10^5\)
\(|d| \le 10000\)
\(|A[i]| \le 10^9\)

这道题我之前讲过分块的做法，具体可以查看我的另一篇博客：C++分块详解
我在这篇博客里吐槽了段错误树懒标记，那我们就学一学懒标记是什么
我们之前写的代码里有一个pushup函数，意思是由子节点的信息更新父节点的信息；我们还是拿上面的线段树举例：假设我要维护线段树每个区间的和，把区间的 \([6, 8]\) 中的数字 \(6\) 变成 \(7\) ，则这段区间的和由 \(6 + 7 + 8 = 21\) 变成了 \(7 + 7 + 8 = 22\)，同时它的所有父节点即 \([6, 10]\)， \([1, 10]\) 的和全都需要更新。时间复杂度为\(O(n)\)；但是我们之前说过，线段树支持的所有操作都可以将时间复杂度控制在\(O(log\ n)\)，那我们该怎么优化它呢？
没错，这就需要我们现在要学的懒标记操作，也称延迟标记。意思就是说，我们可以在线段树的结构体内加上一个标记add，在执行修改命令时，直接将add赋值为我们想要增加的数，表示“这个节点被我修改过，但我还未更新下面的子节点的信息”；后续查询时，我们只需要检查这个节点的父节点有没有背过“懒标记”的锅，如果有，就将这个节点和它父节点的另外一个子节点也标记上懒标记，再清除父节点的懒标记即可。

例题2完整代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 100010;
int n, m;
int w[N];
struct Node {
    int l, r;
    ll sum, add;    //  sum是区间的和，add是区间的懒标记
} tr[N * 4];
void pushup(int u) {
    tr[u].sum = tr[u * 2].sum + tr[u * 2 + 1].sum;
}
void pushdown(int u) {  //  向下传递懒标记
    auto &root = tr[u], &left = tr[u * 2], &right = tr[u * 2 + 1];
    if (root.add) {
        left.add += root.add, left.sum += (ll)(left.r - left.l + 1) * root.add;
        right.add += root.add, right.sum += (ll)(right.r - right.l + 1) * root.add;
        root.add = 0;
    }
}
void build(int u, int l, int r) {
    if (l == r) tr[u] = {l, r, w[r], 0};
    else {
        tr[u] = {l, r};
        int mid = l + r >> 1;
        build(u * 2, l, mid), build(u * 2 + 1, mid + 1, r);
        pushup(u);
    }
}
void modify(int u, int l, int r, int d) {
    if (tr[u].l >= l && tr[u].r <= r) {
        tr[u].sum += (ll)(tr[u].r - tr[u].l + 1) * d;
        tr[u].add += d;
    } else {    //  别忘了分开
        pushdown(u);
        int mid = tr[u].l + tr[u].r >> 1;
        if (l <= mid) modify(u * 2, l, r, d);
        if (r > mid) modify(u * 2 + 1, l, r, d);
        pushup(u);
    }
}
ll query(int u, int l, int r) {
    if (tr[u].l >= l && tr[u].r <= r) return tr[u].sum;
    pushdown(u);
    int mid = tr[u].l + tr[u].r >> 1;
    ll sum = 0;
    if (l <= mid) sum = query(u * 2, l, r);
    if (r > mid) sum += query(u * 2 + 1, l, r);
    return sum;
}
int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
    build(1, 1, n);
    char op[2];
    int l, r, d;
    while (m -- ) {
        scanf("%s%d%d", op, &l, &r);
        if (*op == 'C') {
            scanf("%d", &d);
            modify(1, l, r, d);
        } else {
            printf("%lld\n", query(1, l, r));
        }
    }
    return 0;
}

好啦，那我们的线段树到这里就讲完啦，可以给我一个赞吗uwu