树状数组

都说树状数组思路很难，那我们今天就给他讲个透彻！
前置知识：lowbit 运算
lowbit 的作用就是返回一个数从右往左数的第一个1与他前面所有的0所组成的十进制数
举个例子：
\(114\)这个数转换为二进制为\(1110010\)，而它从右往左数的第一个\(1\)在第二位，将这位右边的所有\(0\)放出来为\(10\)，转换为十进制为\(2\)，所以 lowbit(114) 返回\(2\)。
lowbit的代码：

int lowbit(int x) { return x & -x; }

树状数组的思路

树状数组的基本作用就是维护一个序列的前缀和，如下图：

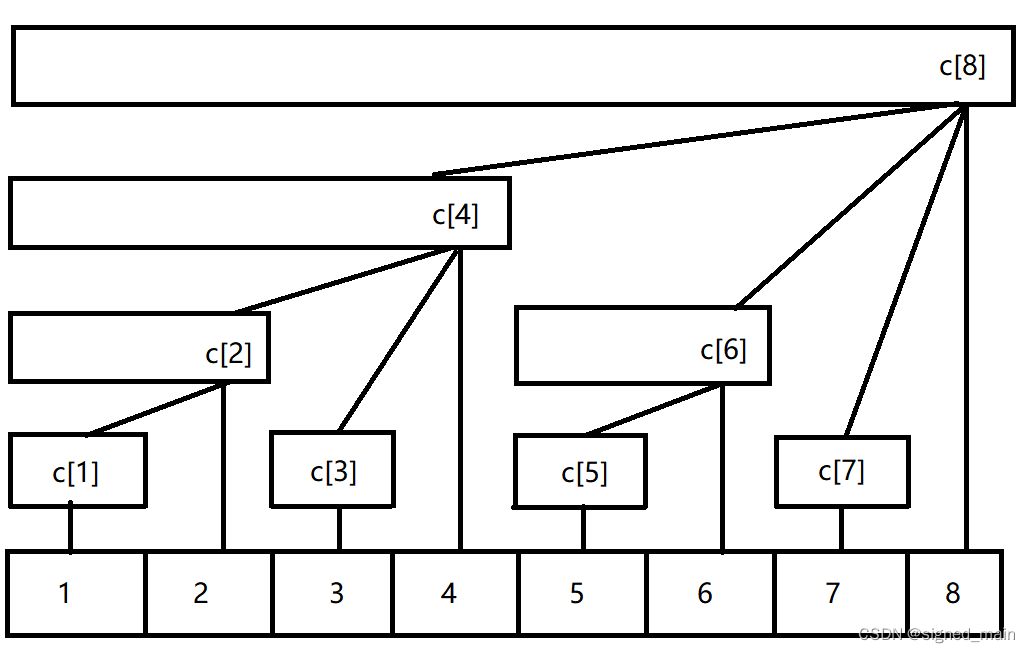
我们先把每个节点下标的二进制数写出来，如下：

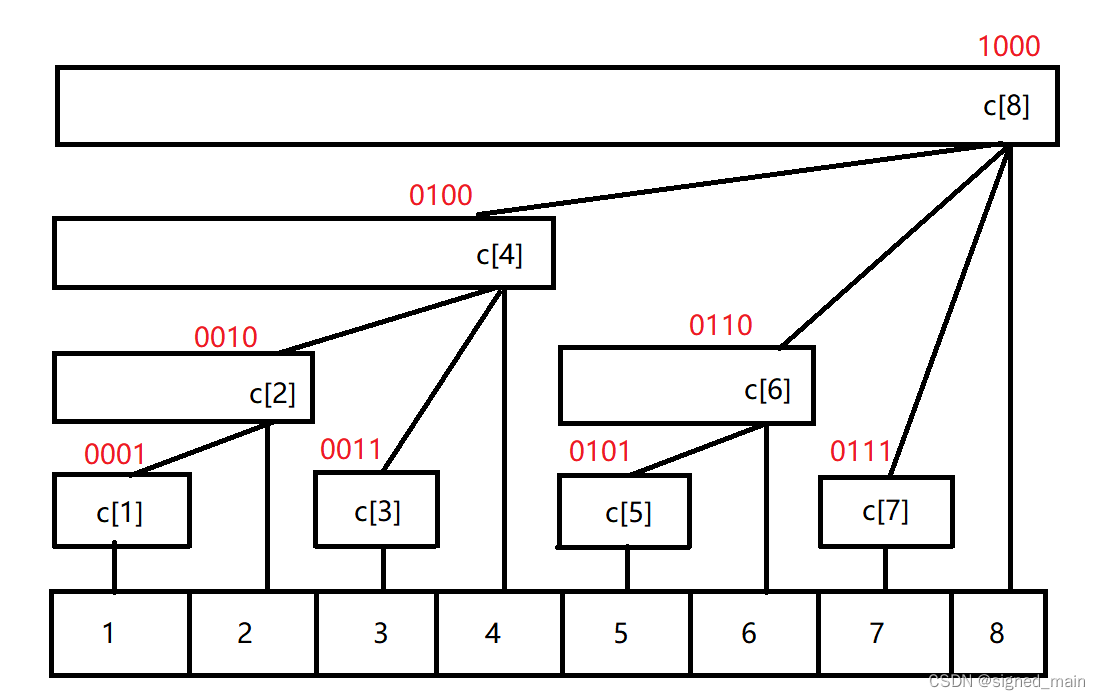
我们可以发现，树状数组有如下性质（注意以下的 x 与 lowbit(x) 均为十进制数）：

1. 每个内部节点 c[x] 保存的是以它为根的子树中所有叶节点的和
2. 每个内部节点 c[x] 的子节点个数为 lowbit(x) 的位数
3. 除根节点外，每个内部节点 c[x] 的父节点为 c[x + lowbit(x)]（下面会经常用到）
4. 树的深度为 \(O(log \ n)\)

接下来我们看看如何对树状数组进行操作

树状数组的操作

---

单点修改

单点修改：把数列中第 \(x\) 个数加 \(d\)
因为我们在子节点增加的值需要向上传递，所以我们这么写修改：

void add(int x, int c) {
    for (int i = x; i <= n; i += lowbit(i))
        tr[i] += c;
    //	每个内部节点 tr[i] 的父节点为 tr[i + lowbit(i)]
}

初始化树状数组

建立一个全为 \(0\) 的数组 tr , 然后对每个位置 x 执行 add(x, a[x]) 即可。

for (int i = 1; i <= n; i++)
    add(i, a[i]);

区间查询

区间查询：求区间的前 \(x\) 项的和（也就是前缀和）
查询的时候我们就每次减掉 lowbit(i) 再相加就可以啦

int sum(int x) {
    int res = 0;
    for (int i = x; i; i -= lowbit(i))
        res += tr[i];
    return res;
}

还有另外一种：求数列中第 \(l \sim r\) 个数的和，这时候我们就可与利用前缀和的性质，即 \(sum[l, r] = sum[1, r] - sum[1, l - 1]\)

cout << sum(r) - sum(l - 1) << '\n';

---

区间修改

区间查询：把数列中第 \(l \sim r\) 个数都加 \(d\) 。
对于区间查询这个操作，我们需要用树状数组维护原序列 a 的差分数组 b，如下：

for (int i = 1; i <= n; i++)
    add(i, a[i] - a[i - 1]); //	add函数在上面有

由于差分数组的性质，我们想要将区间 \([l, r]\) 加上 \(d\) ，就相当于 \(add(l, d)\)、\(add(r + 1, -d)\)。

add(l, d), add(r + 1, -d);

单点查询

求 \(a[x]\) 就相当于求 \(b[1] + b[2] + b[3] + ... + b[x]\)，也就是树状数组 \(1 \sim x\) 的和，直接使用上面的 sum 函数即可

int sum(int x) {
    int res = 0;
    for (int i = x; i; i -= lowbit(i))
        res += tr[i];
    return res;
}

例题

给定长度为 \(N\) 的数列 \(A\)，然后输入 \(M\) 行操作指令。

第一类指令形如 C l r d，表示把数列中第 \(l \sim r\) 个数都加 \(d\)。

第二类指令形如 Q x，表示询问数列中第 \(x\) 个数的值。

对于每个询问，输出一个整数表示答案。

输入格式

第一行包含两个整数 \(N\) 和 \(M\)。

第二行包含 \(N\) 个整数 \(A[i]\)。

接下来 \(M\) 行表示 \(M\) 条指令，每条指令的格式如题目描述所示。

输出格式

对于每个询问，输出一个整数表示答案。

每个答案占一行。

数据范围

\(1 \le N,M \le 10^5\),
\(|d| \le 10000\),
\(|A[i]| \le 10^9\)

输入样例：

10 5
1 2 3 4 5 6 7 8 9 10
Q 4
Q 1
Q 2
C 1 6 3
Q 2

输出样例：

4
1
2
5

这题就属于上面讲解树状数组维护差分数组那一类的，代码：

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>

using namespace std;

typedef long long ll;

const int N = 100010;

int n, m;
int a[N];
ll tr[N];

int lowbit(int x) { return x & -x; }

void add(int x, int c) {
    for (int i = x; i <= n; i += lowbit(i))
        tr[i] += c;
}

ll sum(int x) {
    ll sum = 0;
    for (int i = x; i; i -= lowbit(i))
        sum += tr[i];
    return sum;
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]);

    for (int i = 1; i <= n; i++)
        add(i, a[i] - a[i - 1]);

    while (m--) {
        char op[2];
        int l, r, d;
        scanf("%s%d", op, &l);
        if (*op == 'C') {
            scanf("%d%d", &r, &d);
            add(l, d), add(r + 1, -d);
        } else
            printf("%lld\n", sum(l));
    }

    return 0;
}

最后说一句：对于那些需要即需要区间查询又需要区间修改的题，还是建议直接使用线段树，可以参考一下我的线段树讲解：C++线段树详解。