前缀和

前缀和

现在有一道题：

输入一个长度为 \(n\) 的整数序列。

接下来再输入 \(m\) 个询问，每个询问输入一对 \(l, r\)。

对于每个询问，输出原序列中从第 \(l\) 个数到第 \(r\) 个数的和。

数据范围

\(1 \le l \le r \le n\)
\(1 \le n,m \le 100000\)
\(-1000 \le 数列中元素的值 \le 1000\)

这种题大家一看就知道打暴力，确实是个好方法 ：

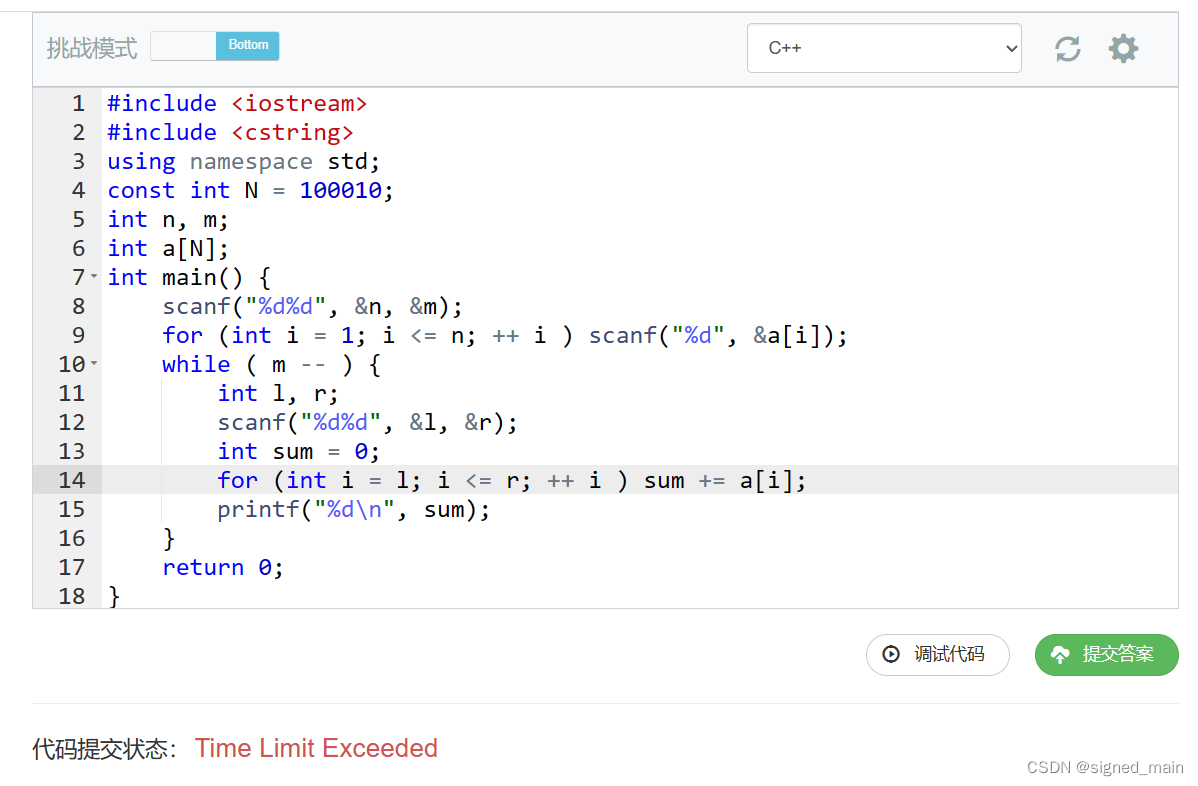
那么我们该如何优化它呢？
我们维护一个名为 \(s\) 的前缀和数组，且 \(s[i] = \sum\limits _ {j = 1}^{i} a[j]\)，如下：

for (int i = 1; i <= n; ++i)
    s[i] = s[i - 1] + a[i];

如果我们维护的序列是 \(1,2,3,4,5,6,7,8,9,10\) 的话，那么我们的前缀和数组为 \(1,3,6,10,15,21,28,36,45,55\) ，那我们该如何利用前缀和数组的性质求和呢？
可以看下面的图：

假如说我们要求 \([l, r]\) 数值的和，我们只需要将 \(s[r]\) （红色部分）减去 \(s[l - 1]\) （蓝色部分）即可。代码：

printf("%d\n", s[r] - s[l - 1]);

完整代码：

#include <cstring>
#include <iostream>
using namespace std;
const int N = 100010;
int n, m;
int a[N];
int s[N];
int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++i)
        scanf("%d", &a[i]);
    for (int i = 1; i <= n; ++i)
        s[i] = s[i - 1] + a[i];
    while (m--) {
        int l, r;
        scanf("%d%d", &l, &r);
        printf("%d\n", s[r] - s[l - 1]);
    }
    return 0;
}

二维前缀和

题目：

输入一个 \(n\) 行 \(m\) 列的整数矩阵，再输入 \(q\) 个询问，每个询问包含四个整数 \(x_1, y_1, x_2, y_2\)，表示一个子矩阵的左上角坐标和右下角坐标。

对于每个询问输出子矩阵中所有数的和。

数据范围

\(1 \le n,m \le 1000\)
\(1 \le q \le 200000\)
\(1 \le x_1 \le x_2 \le n\)
\(1 \le y_1 \le y_2 \le m\)
\(-1000 \le 矩阵内元素的值 \le 1000\)

二维前缀和，可以用来求一个矩阵里人任意一个子矩阵内数的和。
我们用 \(s[I][J]\) 表示 \(\sum\limits_{i = 1}^{I} \sum\limits_{j = 1}^{J} a[i][j]\)。
所以\(s[I][J]（绿色部分） = s[I - 1][J]（蓝色部分） + s[I][J - 1]（红色部分） - s[I - 1][J - 1] （紫色部分）+ a[I][J]\)

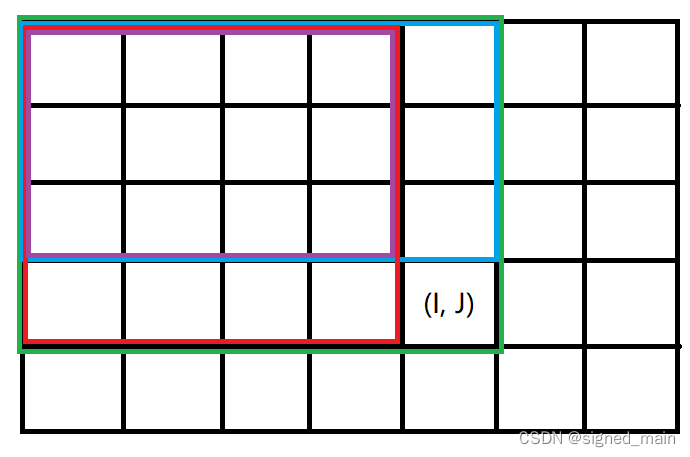
查询的话，我们将上面所有颜色的框改一下位置就好了；假如我们要求 \((x_1, y_1)\) 到 \((x_2, y_2)\) 的和，即：\(s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]\)
代码：

#include <cstring>
#include <iostream>
using namespace std;
const int N = 1010;
int n, m, q;
int a[N][N];
int s[N][N];
int main() {
    scanf("%d%d%d", &n, &m, &q);
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= m; ++j)
            scanf("%d", &a[i][j]);
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= m; ++j)
            s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
    while (q--) {
        int x1, y1, x2, y2;
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        printf("%d\n",
               s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
    }
    return 0;
}