Python - 面向对象编程 - MRO 方法搜索顺序
为什么会讲 MRO？
- 在讲多继承的时候：https://www.cnblogs.com/poloyy/p/15224912.html
- 有讲到， 当继承的多个父类拥有同名属性、方法，子类对象调用该属性、方法时会调用哪个父类的属性、方法呢？
- 这就取决于 Python 的 MRO 了
什么是 MRO
- MRO，method resolution order，方法搜索顺序
- 对于单继承来说，MRO 很简单，从当前类开始，逐个搜索它的父类有没有对应的属性、方法
- 所以 MRO 更多用在多继承时判断方法、属性的调用路径
- Python 中针对类提供了一个内置属性 __mro__ 可以查看方法搜索顺序
实际代码
class A: def test(self): print("AAA-test") class B: def test(self): print("BBB-test")
# 继承了三个类，B、A、还有默认继承的 object class C(B, A): ... # 通过类对象调用，不是实例对象！ print(C.__mro__) # 输出结果 (<class '__main__.C'>, <class '__main__.B'>, <class '__main__.A'>, <class 'object'>)
- 在搜索方法时，是按照 __mro__ 的输出结果从左往右的顺序查找的
- 如果在当前类（Class C）中找到方法，就直接执行，不再搜索
- 如果没有找到，就查找下一个类中（Class B）是否有对应的方法，如果找到，就直接执行，不再搜素
- 如果找到最后一个类（Class object）都没有找到方法，程序报错
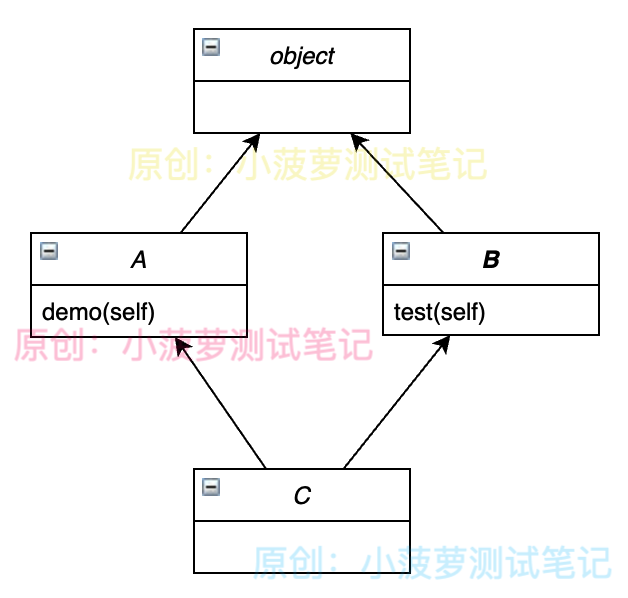
类图
注意
其实 MRO 是涉及一个底层算法的，下面来详细讲解一下
MRO 算法
Python 发展到现在经历了三种算法
- 旧式类 MRO 算法：从左往右，采用深度优先搜索（DFS），从左往右的算法，称为旧式类的 MRO
- 新式类 MRO 算法：自 Python 2.2 版本开始，新式类在采用深度优先搜索算法的基础上，对其做了优化
- C3 算法：自 Python 2.3 版本，对新式类采用了 C3 算法；由于 Python 3.x 仅支持新式类，所以该版本只使用 C3 算法
什么是旧式类，新式类
https://www.cnblogs.com/poloyy/p/15226425.html
想深入了解 C3 算法的可以看看官网
https://www.python.org/download/releases/2.3/mro/
旧式类 MRO 算法
需要在 python2 环境下运行这段代码
实际代码
# 旧式类算法 class A: def test(self): print("CommonA") class B(A): pass class C(A): def test(self): print("CommonC") class D(B, C): pass D().test() # python2 下的运行结果 CommonA
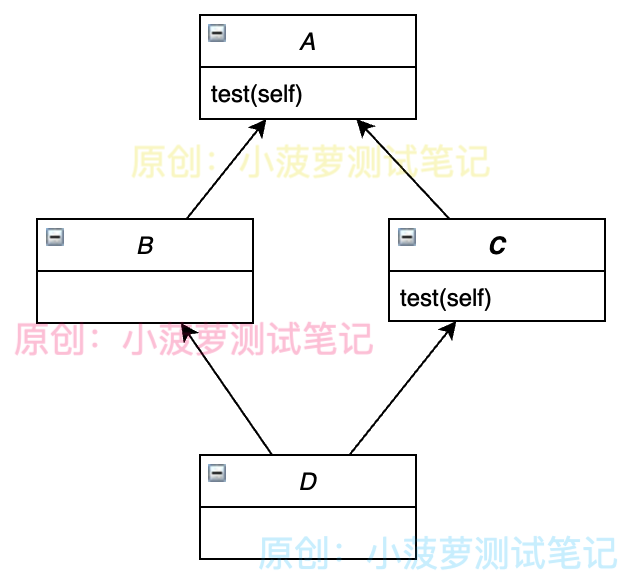
类图
分析
- 通过类图可以看到，此程序中的 4 个类是一个“菱形”继承的关系
- 当使用 D 类实例对象访问 test() 方法时，根据深度优先算法，搜索顺序为 D->B->A->C->A
- 因此，旧式类 MRO 算法最先搜索得到 test() 方法是在 A 类里面，所以最终输出结果为 CommonA
新式类 MRO 算法
- 为解决旧式类 MRO 算法存在的问题，Python 2.2 版本推出了新的计算新式类 MRO 的方法
- 它仍然采用从左至右的深度优先遍历，但是如果遍历中出现重复的类，只保留最后一个
以上面的代码栗子来讲
- 深度优先遍历，搜索顺序为 D->B->A->C->A
- 因为顺序中有 2 个 A，因此只保留最后一个
- 最终搜索顺序为 D->B->C->A
新式 MRO 算法的问题
虽然解决了旧式 MRO 算法的问题，但可能会违反单调性原则
什么是单调性原则？
在子类存在多继承时，子类不能改变父类的 MRO 搜索顺序，否则会导致程序发生异常
实际代码
class X(object): pass class Y(object): pass class A(X, Y): pass class B(Y, X): pass class C(A, B): pass
- 深度优先遍历后的搜索顺序为： C->A->X->object->Y->object->B->Y->object->X->object
- 相同取后者的搜索顺序为： C->A->B->Y->X->object
分析不同类的 MRO
- A： A->X->Y->object
- B： B->Y->X->object
- C： C->A->B->X->Y->object
很明显，B、C 中间的 X、Y 顺序是相反的，就是说 B 被继承时，它的搜索顺序会被改变
在 python2 中运行这段代码的报错
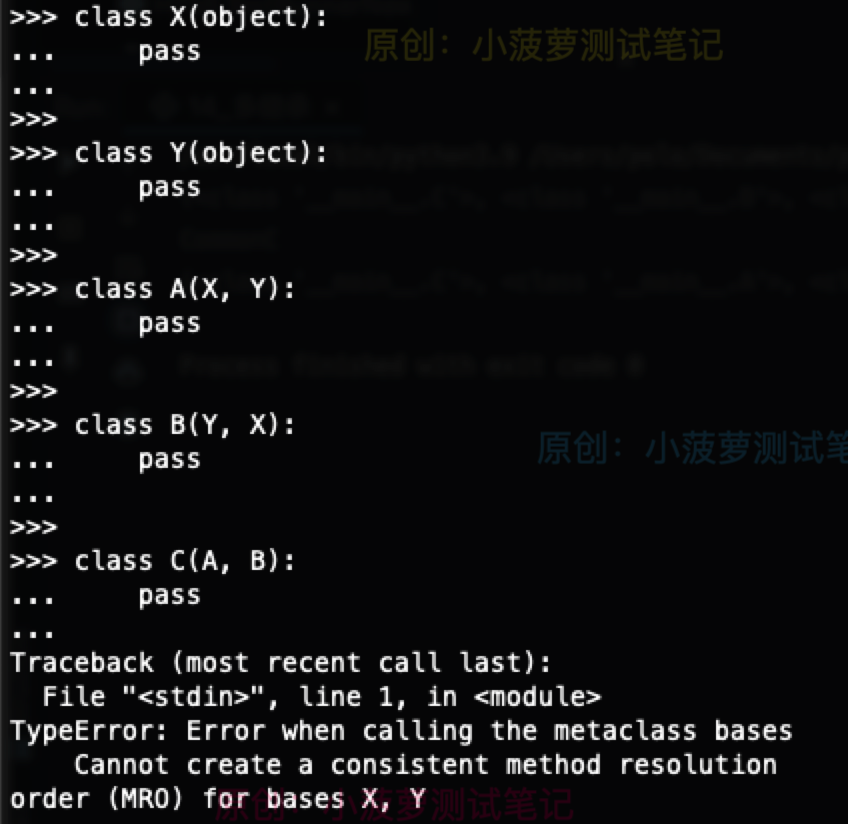
在 python3 中运行这段代码的报错
C3 MRO 算法
- 为解决前面两个算法的问题，Python 2.3 采用了 C3 方法来确定方法搜索顺序
- 多数情况下，如果别人提到 Python 中的 MRO，指的都是 C3 算法
将上面第一个栗子的代码放到 python3 中运行
class A: def test(self): print("CommonA") class B(A): pass class C(A): def test(self): print("CommonC") class D(B, C): pass D().test() # 输出结果 CommonC
简单了解下 C3 算法
以上面代码为栗子，C3 会把各个类的 MRO 等价为以下等式
- A：L[A] = merge(A , object)
- B：L[B] = B + merge(L[A] , A)
- C：L[C] = C + merge(L[A] , A)
- D：L[D] = D + merge(L[B] , L[C] , B , C)
了解一下：头、尾
以 A 类为栗，merge() 包含的 A 成为 L[A] 的头，剩余元素（这里只有 object）称为尾
merge 的运算方式
- 将 merge 第一个列表的头元素（如 L[A] 的头），记作 H
- 如果 H 出现在 merge 其他列表的头部，则将其输出，并将其从所有列表中删除
- 如果 H 只出现一次，那么也将其输出，并将其从所有列表中删除
- 如果 H 出现在 merge 其他列表的非头部，则取下一个列表的头元素记作 H，然后回到步骤二
- 最后回到步骤一，重复以上步骤
重复以上步骤直到列表为空，则算法结束；如果不能再找出可以输出的元素，则抛出异常
简单类 MRO 的计算栗子
class B(object): pass print(B.__mro__) (<class '__main__.B'>, <class 'object'>)
MRO 计算方式
L[B] = L[B(object)] = B + merge(L[object]) = B + L[object] = B object
单继承 MRO 的计算栗子
# 计算 MRO class B(object): pass class C(B): pass print(C.__mro__) (<class '__main__.C'>, <class '__main__.B'>, <class 'object'>)
MRO 计算方式
L[C] = C + merge(L[B]) = C + L[B] = C B object
多继承 MRO 的计算栗子
O = object class F(O): pass class E(O): pass class D(O): pass class C(D, F): pass class B(D, E): pass class A(B, C): pass print(C.__mro__) print(B.__mro__) print(A.__mro__) # 输出结果 (<class '__main__.C'>, <class '__main__.D'>, <class '__main__.F'>, <class 'object'>) (<class '__main__.B'>, <class '__main__.D'>, <class '__main__.E'>, <class 'object'>) (<class '__main__.A'>, <class '__main__.B'>, <class '__main__.C'>, <class '__main__.D'>, <class '__main__.E'>, <class '__main__.F'>, <class 'object'>)
O 类、object 类 MRO 计算
L[O] = O = object
D、E、F 类 MRO 计算
L[D] = D + merge(L[O])
= D O
C 类 MRO 计算
L[C] = L[C(D, F)] = C + merge(L[D], L[F], DF) # 从前面可知 L[D] 和 L[F] 的结果 = C + merge(DO, FO, DF) # 因为 D 是顺序第一个并且在几个包含 D 的 list 中是 head， # 所以这一次取 D 同时从列表中删除 D = C + D + merge(O, FO, F) # 因为 O 虽然是顺序第一个但在其他 list (FO)中是在尾部, 跳过 # 改为检查第二个list FO # F 是第二个 list 和其他 list 的 head # 取 F 同时从列表中删除 F = C + D + F + merge(O) = C D F O
B 类 MRO 计算
L[B] = L[B(D, E)] = B + merge(L[D], L[E], DE) = B + merge(DO, EO, DE) = B + D + merge(O, EO, E) = B + D + E + merge(O) = B D E O
A 类 MRO 计算
L[A] = L[A(B,C)] = A + merge(L[B], L[C], BC) = A + merge( BDEO, CDFO, BC ) = A + B + merge( DEO, CDFO, C ) # D 在其他列表 CDFO 不是 head，所以跳过到下一个列表的 头元素 C = A + B + C + merge( DEO, DFO ) = A + B + C + D + merge( EO, FO ) = A + B + C + D + E + merge( O, FO ) = A + B + C + D + E + F + merge( O ) = A B C D E F O
多继承 MRO 的计算栗子二
O = object class F(O): pass class E(O): pass class D(O): pass class C(D, F): pass class B(E, D): pass class A(B, C): pass print(C.__mro__) print(B.__mro__) print(A.__mro__) # 输出结果 (<class '__main__.C'>, <class '__main__.D'>, <class '__main__.F'>, <class 'object'>) (<class '__main__.B'>, <class '__main__.E'>, <class '__main__.D'>, <class 'object'>) (<class '__main__.A'>, <class '__main__.B'>, <class '__main__.E'>, <class '__main__.C'>, <class '__main__.D'>, <class '__main__.F'>, <class 'object'>)
O 类、object 类 MRO 计算
L[O] = O = object
D、E、F 类 MRO 计算
L[D] = D + merge(L[O])
= D O
C 类 MRO 计算
L[C] = L[C(D, F)] = C + merge(L[D], L[F], DF) = C + merge(DO, FO, DF) = C + D + merge(O, FO, F) = C + D + F + merge(O) = C D F O
B 类 MRO 计算
L[B] = L[B(E, D)] = B + merge(L[E], L[D], ED) = B + merge(EO, DO, ED) = B + E + merge(O, DO, D) = B + E + D + merge(O) = B E D O
A 类 MRO 计算
L[A] = L[A(B, C)] = A + merge(L[B], L[C], BC) = A + merge(BEDO, CDFO, BC) = A + B + merge(EDO, CDFO, C) = A + B + E + merge(DO,CDFO, C) = A + B + E + C + merge(O,DFO) = A + B + E + C + D + merge(O, FO) = A + B + E + C + D + F + merge(O) = A B E C D F O
