浅谈数据结构-归并排序

归并算法采用分治法，利用二叉树的概念来实现排序算法，建立在递归合并操作的基础上算法。通过将数组分组到两个序列，排序，然后在归并排序，进而实现算法。归并排序算法就是利用归并的思想实现的排序算法。

一、算法思想

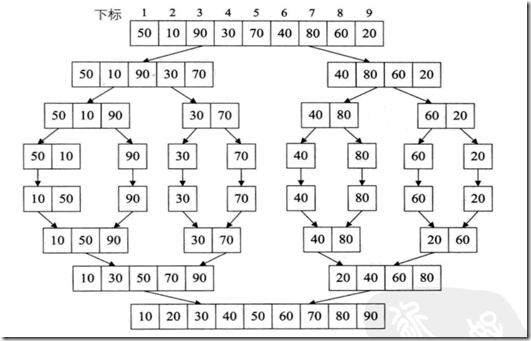
数组序列{16, 7, 13, 10, 9, 15, 3, 2, 5, 8, 12, 1, 11, 4, 6, 14}，利用一定的交换排序，得到有序的小序列后，进行两两合并排序后再合并，最终获得一个有序的数组。从形状上开像极了一棵倒置的完全二叉树

    它的原理是假设初始序列含有n个记录，则可以看成是n个有序的子序列，每个子序列的长度为1，然后两两再归并，得到|n/2|（|x|表示不小于x的最小整数）个长度为2或1的有序子序列；再两两归并，......，如此重复，直至得到一个长度为n的有序序列为止，这种排序方法称为2路归并排序。

归并排序其实要做两件事：

（1）“分解”——将序列每次折半划分。

（2）“合并”——将划分后的序列段两两合并后排序。

二、代码

//归并排序
inline void SortAlgorithm::MergeSort(int *pLarray,int *pRarray,int start ,int length)
{
    //因为是二叉树概念，长度为一般，跨度合并的话就是步长
    int i = 1;
    int j;
    while(i <= length - 2*start +1)
    {
        Merge(pLarray,pRarray,i,i+start-1,i+2*start-1);   //两两合并
        i = i+2*start;
    }
    if (i < length-start+1)   //归并最后两个序列，此处为length，注意点
    {
        Merge(pLarray,pRarray,i,i+start-1,length);
    }
    else
        for(j = i;j<= length;j++)    //如果剩下最后序列
            pRarray[j] = pLarray[j];
}
inline void SortAlgorithm::Merge(int *pLaray,int *pRarray,int start,int length1,int length2)
{
    int j,k ,l;
    for (k = start,j = length1+1;start<=length1&&j<=length2;k++)   //夸组将相应的元素进行合并
    {
        //左边的数小于右边数，将小的数填入目标数组
        if (pLaray[start] < pLaray[j])
        {
            pRarray[k] = pLaray[start];
            start++;
        }
        else
        {
            pRarray[k] = pLaray[j];
            j++;
        }
    }
    if (start <=length1)  //将剩余的填入到目标数组中
    {
        for (l = 0;l<=length1-start;l++)
        {
            pRarray[l+k] = pLaray[start+l];
        }
    }
    if (j <= length2)
    {
        for(l = 0; l <= length2 - j; l++)
        {
            pRarray[l+k] = pLaray[j+l];      //将剩余的sr[j...n]复制到tr 
        }
    }
}

//归并排序
void SortAlgorithm::MergeSort(pSqlList pList)
{
    //申请空间，存储合并后的有序数组
    int *Array = new int[10];
    
    memset(Array,0,pList->length);
    int k =1;
    while(k < pList->length)
    {
        //合并序列，从序列大小为1开始，然后2，4，8，
        MergeSort(pList->SqlArray,Array,k,pList->length-1);
        k = k*2;
        MergeSort(Array,pList->SqlArray,k,pList->length-1);
        k = k*2;
        for (int  i =0;i<pList->length;i++)
        {
            printf("%d\t",Array[i]);
        }
        PrintSqlList(pList);
        printf("\n");
    }
}

三、代码分析

 

 

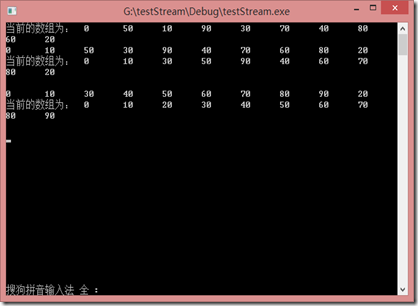
程序结果如上图，分析则为下面两幅图

步骤：

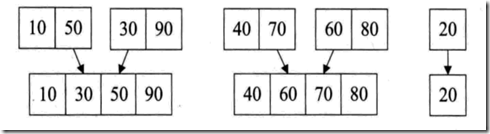
1、首先是两两进行交换合并，形成初步有序小序列

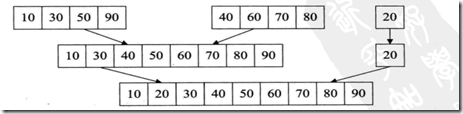
2、然后再讲刚才的两两有序序列进行再次合并，形成四组，其中关键代码在Merge函数中。

3、程序一定注意数组的起止点，还有数组长度等问题，比如，本数组是9个数据，最后是8个元素和1个元素合并，后面调用merge时，为length。