浅谈数据结构-选择排序(简单、堆排序）

选择排序：每趟从待排序的记录中选出关键字最小的记录，顺序放在已排序的记录序列末尾，直到全部排序结束为止。

选择排序正如定义所讲，在数组查询出最小值，然后放在此次循环开始位置（前一次循环已经获取比它更小的值放在前面）。

简单选择排序就是单纯的从数组中一次一次循环获取到最小值，放到循环位置。而堆排序正如名字，是从一个堆中选择，然后放在堆的循环开始位置，所以重点就是如何争取获取堆（分组）。

一、简单选择排序

1、算法思想

正如图上所示，每次选择最小值，然后放在本次循环的开始位置。

2、代码

//选择排序
void SortAlgorithm::SelectSort(pSqlList pList)
{
    int i,j,min;
    printf("开始验证选择排序");
    //选择排序和低级冒泡排序很像，关键就是在比较时，低级冒泡进行数据交换，而选择排序进行记录，最后只交换一次
    for (i =0;i<pList->length;i++)
    {
        min = i;
        for(j = pList->length-1;j>=i;j--)
        {
            //注意数组坐标，千万别溢出
            if (pList->SqlArray[min] > pList->SqlArray[j])
            {
                min = j;
            }
        }
        //最后进行交换，先选择最小的，最后一次交换
        swap(pList,i,min);
        PrintSqlList(pList);
    }


}

简单选择排序算法海华丝比较简单，关键点就是遍历寻找最小记录，然后入循环开始位置进行交换。

二、堆排序

1、堆排序概念

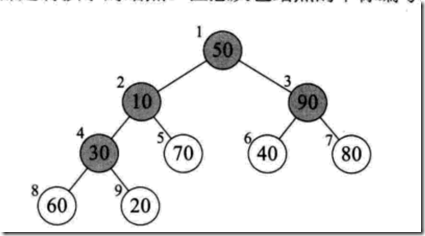
堆排序是首先引入完全二叉树的概念，就是构建完全二叉树，前提是完全二叉树是有特点的，也就是大根堆和小根堆。

上图是完全二叉树，在完全二叉树中有几个性质：

设当前元素在数组中以R[i]表示，那么，
(1) 它的左孩子结点是：R[2*i+1];
(2) 它的右孩子结点是：R[2*i+2];
(3) 它的父结点是：R[(i-1)/2];

(4) R[i] <= R[2*i+1] 且 R[i] <= R[2i+2]。

大根堆：每个结点的关键字都不小于其孩子结点的关键字。

小根堆：每个结点的关键字都不大于其孩子结点的关键字。

2、算法思想

（1）根据初始数组去构造初始堆，默认是大根堆（构建一个完全二叉树，保证所有的父结点都比它的孩子结点数值大）。

（2）每次交换第一个和最后一个元素，输出最后一个元素（最大值），然后把剩下元素重新调整为大根堆。

上述算法是个循环操作，先构建，然后交换输出，最后调整余下的为大根堆，其实就是寻找最大值，其实只需要左右两个结点，那个比较大，就获取那个，所以调整堆排序也是比较简单，就是比较左右结点，获取最大值

第一步：构建大根堆

第二步、输出、调整

3、代码

////堆排序
void SortAlgorithm::HeapSort(pSqlList pList)
{
    //循环构建堆
    for (int i = pList->length/2;i>0;i--)
    {
        AdjustHeap(pList,i,pList->length-1);
    }
    PrintSqlList(pList);
    for (int i = pList->length-1;i>1;i--)
    {
        //循环输出根节点，同时再次调整为大根堆
        swap(pList,1,i);     //根节点位于最前面，也就是1，这样就将1最大值，放在数组后面了
        AdjustHeap(pList,1,i-1);
        PrintSqlList(pList);
    }
}
inline void SortAlgorithm::AdjustHeap(pSqlList pList,int start,int length)
{
    int temp  = pList->SqlArray[start];  //这是分支节点，然后比较它的分支节点，也就是2i
    for (int i = 2*start;i<length;i = i*2)
    {
        //获取左右结点中比较大的值的坐标
        if (i<length && pList->SqlArray[i] < pList->SqlArray[i+1])
        {
            i++;
        }
        //如果根节点本来就大，无序调整
        if (temp > pList->SqlArray[i])
        {
            break;
        }
        //交换值，将左右结点大值放在根节点
        pList->SqlArray[start] = pList->SqlArray[i];
        start = i;

    }
    //将开始需要比较的值，放在最后交换出的位置上
    pList->SqlArray[start] = temp;

}

4、代码分析

程序中一开始构建，调整大根堆，最大值是length/2，因为从完全二叉树的概念上分析：

在上图中大根堆的建立，就是调整前四个元素的位置，就是放再分支节点上还是叶子结点上，所以只要输入4即可。

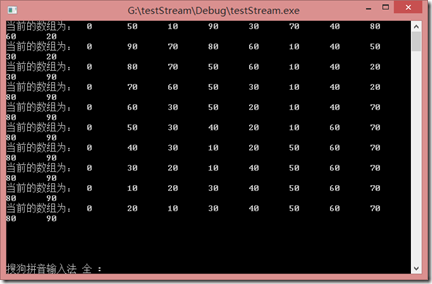
一开始大根堆，发现是90在最前面。

首先，将位于第一位（根节点树最大），然后和最后一位交换，然后调整前8位（第九位已经是最大了）。

然后，再讲获取到的80，和最后一位（第九位，第十已经不需交换），然后调整前7位，当然都是从1开始了。

最后经过一次次循环调整，完成算法的排序。

其中关键的思想是获取调整堆排序，比如一开始90和20交换后，20位于第一位置；此时20和左右结点中的较大值80交换，关键是后续继续拿20和后面左右结点比较，直到break，也就是找到比它小的，跳出，然后赋值。

三、性能分析

1、简单选择排序

从简单选择排序的过程来看，它最大的特点就是交换移动数据次数相当少，这样也就节约了相应的时间。分析它的时间复杂度，无论最好最差的情况，其比较次数都是一样多，第i趟排序需要进行n-i次关键字的比较，此时需要n-1 +...+1 = n(n - 1)/2次。而对于交换次数而言，当最好的时候，交换次数为0，最差的时候，也就初始降序时，交换次数为n-1次。总的时间复杂度依然为O(n²)。

    尽管简单选择排序与冒泡排序同为O(n²)，但简单选择排序的性能上还是要优于冒泡排序的。

2、堆排序

堆排序是一种不稳定的排序方法。

因为在堆的调整过程中，关键字进行比较和交换所走的是该结点到叶子结点的一条路径。

在程序运行时主要消耗在初始化构建堆和重建堆的反复刷选上。在初始化构建堆时，是从非终结点开始，其实比较两次，本来时n/2，这样最多对n/2进行两次比较工作，所以初始化构建大根堆是O(n)。

在调整构建堆时，第i次构建树logI（根据完全二叉树性质），需要遍历N-1记录,所以时间复杂度是O(nlogn)