浅谈数据结构-插入排序(直接插入、希尔排序)
插入排序:数组中获取数据,遍历数组中数据进行比较,找到合适位置,进行插入工作。
直接插入和希尔排序关键区别在于:希尔排序是有分组,然后进行迭代,组间插入数据,是一种变形的插入排序算法。
一、直接插入法
1、算法思想

上图是一张扑克牌,在摸牌阶段就是直接插入操作。
(1) 数组中下标为1 的元素视为元素个数为 1 的有序序列。(元素0表示哨兵)
(2) 然后,我们要依次把 R1, R2, ... , RN-1 插入到这个有序序列中。所以,我们需要一个外部循环,从下标 1 扫描到 N-1 。
(3) 接下来描述插入过程。假设这是要将 Ri 插入到前面有序的序列中。由前面所述,我们可知,插入Ri时,前 i-1 个数肯定已经是有序了。
2、算法代码
//插入排序 void SortAlgorithm::InsertSort(pSqlList pList) { //插入排序,有哨兵概念 int i,j; printf("开始验证插入排序"); for (i =1;i<pList->length-1;i++) { //遍历获取数组中元素,如果后续元素比较小,进行插入工作,插到这个元素左边,如果大,继续循环 if (pList->SqlArray[i+1] < pList->SqlArray[i]) { //在数组中0位置为哨兵作用,获取此次较小元素 pList->SqlArray[0] = pList->SqlArray[i+1]; //再将较小元素,和之前元素比较,如果发现较大的,停止,然后插入 for (j = i;j>0 && pList->SqlArray[0] < pList->SqlArray[j];j--) { //向后移动数据,让其有空间插入工作,第一个是插到i+1位置,就是较小元素的位置 pList->SqlArray[j+1] = pList->SqlArray[j]; } //插入工作,因为j--,此处是j+1 pList->SqlArray[j+1] = pList->SqlArray[0]; } PrintSqlList(pList); } }
3、代码分析
上图就是程序运行结果:首相数组是{0,50,10,90,30,70,40,80,20}
1、先开始找无序的数,发现50>10,那么选取10作为基准值,开始进行插入操作。
2、从10坐标往前遍历,要将10的插入正确位置。向前遍历(比10大,继续向前寻找),当发现比10小,停止,进行插入工作。
3、插入工作将是向后移动数据,此时50和10交换位置。第一循环停止。
4、比较50与90,是有序的,下一条记录。
5、比较90和30,发现30<90进入插入工作,将30插入到{10,50,90}有序序列中,输出的就是{30,10,30,50,90,70,40,80,20}
6、比较90和70,同样道理,最后输出争取结果。关键在于向有序数组中,判断插入到正确位置。
代码实现上有冒泡算法的影子,就是前后元素比较,此处不是交换,而是向前的有序数组进行插入工作。
二、希尔排序
希尔排序是一种变异的插入算法,在引入二叉树的概念后(分组,每次遍历组的大小变化,同时是夸组插入,将可能比较大的元素交叉插入到后面组,较小的插入前面组),遵循先粗分再细分的原则,实现交叉插入。
1、算法思想
插入算法基于分组交叉插入,首先第一步是分组,确定分组大小。然后在组间进行插入工作,所以插入时的步长为分组大小。
上图来源于网络,很少说明了希尔排序算法的精髓,交叉插入工作。
在第一趟排序中,我们不妨设 gap1 = N / 2 = 5,即相隔距离为 5 的元素组成一组,可以分为 5 组。
接下来,按照直接插入排序的方法对每个组进行排序。
在第二趟排序中,我们把上次的 gap 缩小一半,即 gap2 = gap1 / 2 = 2 (取整数)。这样每相隔距离为 2 的元素组成一组,可以分为 2 组。
按照直接插入排序的方法对每个组进行排序。
在第三趟排序中,再次把 gap 缩小一半,即gap3 = gap2 / 2 = 1。 这样相隔距离为 1 的元素组成一组,即只有一组。
按照直接插入排序的方法对每个组进行排序。此时,排序已经结束。
需要注意一下的是,图中有两个相等数值的元素 5 和 5 。我们可以清楚的看到,在排序过程中,两个元素位置交换了。
2、希尔排序的步长
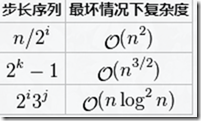
已知的最好步长序列是由Sedgewick提出的(1, 5, 19, 41, 109,...),该序列的项来自
这两个算式。
当增量序列为dlta[k]=2t-k+1 (0<=k<=t<=|log(n+1)|)时,可以获得不错的效果。其时间复杂度为O(n3/2),要好于直接排序。
这项研究也表明“比较在希尔排序中是最主要的操作,而不是交换。”用这样步长序列的希尔排序比插入排序和堆排序都要快,甚至在小数组中比快速排序还快,但是在涉及大量数据时希尔排序还是比快速排序慢。
3、程序代码
//希尔排序 void SortAlgorithm::ShellSort(pSqlList pList) { //希尔排序是插入排序的改进,先分组,再插入,而且插入是夸组插入。先有分组,在执行插入 int i,j; printf("开始验证希尔排序"); int increment = pList->length; do { //小于3,时,保证能循环 increment = increment/3 +1; //增量寻列 //执行夸组插入工作,跨度大小为increment,所以j的跨度就是increment for (i = increment +1;i<pList->length;i++) { //从组的后部分和前部分比较,如果后面小,进行夸组插入工作 if (pList->SqlArray[i] < pList->SqlArray[i-increment]) { //和插入排序很像 pList->SqlArray[0] = pList->SqlArray[i]; for( j = i-increment;j>0&&pList->SqlArray[0]<pList->SqlArray[j];j = j-increment) { //比较大移动后面 pList->SqlArray[j+increment] = pList->SqlArray[j]; } pList->SqlArray[j+increment] = pList->SqlArray[0]; } } PrintSqlList(pList); } while (increment>1); }
4、代码分析
上述代码中while跳出条件是步长大于1,同时在进行插入工作是,是j=j-increment,这样才实现交叉插入,向右移动步长也是j+increment
在程序中输入的数组为:{0,50,10,90,30,70,40,80,60,20}。步长为4,所以应该是坐标为1的和坐标为5的进行交叉比较,插入。
首先步长为4,50和70比较,50<70,不变,i++。然后10与40,后来到90和80交换,30和60不交换,最后是70和20交换,这是发现位置1为50,50和20,继续交换,最后结果就是{20,20,20,80,30,50,40,90,60,70}。
第二次,此时incerment = incerment/3+1,此时incerment为2,说明步长为2,意味坐标1和坐标3之间交叉比较,进行插入。当然往后1,3,5也是需要判断的。
第三次继续,因为increment =2,继续循环,此时incerment是1,意味两两交叉交换插入了,但此时序列是基本有序了,之间数据交换很小了。
三、算法分析
1、直接插入排序复杂度
从空间上看,只需要 一个记录的辅助空间,空间的复杂度为O(1),当最好的情况下,也就是数组是有序表,没有移动记录时间复杂度为O(n)。
最坏的情况是,排序表是逆序,此时需要比较1+3+4+5+6….n-1 = (n+2)(n-1)/2,时间复杂度为O(n2).同样的O(n2)时间复杂度,直接插入排序法比冒泡排序和简单选择排序的性能要好一些。
所以,数据越接近正序,直接插入排序的算法性能越好。
2、希尔排序复杂度分析
希尔排序中步长选择很重要,Donald Shell 最初建议步长选择为N/2并且对步长取半直到步长达到1。虽然这样取可以比O(N2)类的算法(插入排序)更好,但这样仍然有减少平均时间和最差时间的余地。可能希尔排序最重要的地方在于当用较小步长排序后,以前用的较大步长仍然是有序的。
研究证明希尔排序最好情况是O(nlogn),最坏的情况是O(n*n0.5),所以比插入排序效果还是好的。