浅析数据结构-图的遍历

上一篇了解图的基本概念，包括图的分类、术语以及存储结构。本篇就是应用图的存储结构，将图进行数据抽象化，应用遍历方法，对数据进行遍历。由于图复杂的数据结构，一定保证图中所有顶点被遍历。如果只访问图的顶点而不关注边的信息，那么图的遍历十分简单，使用一个foreach语句遍历存放顶点信息的数组即可。但是，如果为了实现特定算法，就必须要根据边的信息按照一定的顺序进行遍历。图的遍历算法是求解图的连通性问题、拓扑排序和求解关键路径等算法的基础。

一、图的遍历

 

图的数据结构相对树复杂，图的任一顶点都可能和其余顶点相邻接，所以在访问了某顶点之后，可能顺着某条边又访问到了已访问过的顶点。在图遍历过程中，防止同一个顶点被访问多次，必须记下每个访问过的顶点。给顶点附加一个访问标志isVisited，其初值为false，一旦某个顶点被访问，则将其isVisited标志设为true。

图顶点数据结构

 

在上面代码图顶点的数据结构定义中，增加了一个bool类型的成员isVisited，用于在遍历时判断是否已经访问过了该顶点。一般在进行遍历操作时，会首先将所有顶点的isVisited属性置为false，访问后设置为true。

图的遍历方法主要有两种：一种是深度优先搜索遍历（Depth-First Search，DFS），另一种是广度优先搜索遍历（Breadth-First Search，BFS）。

二、深度优先搜索遍历

原理

图的深度优先遍历类似于二叉树的深度优先遍历，其基本思想是：从图中某个顶点v出发，访问此顶点，然后从v的未被访问的邻接点出发深度优先遍历图，直至图中所有和v有路径相通的顶点都被访问到。显然，这是一个递归的搜索过程。

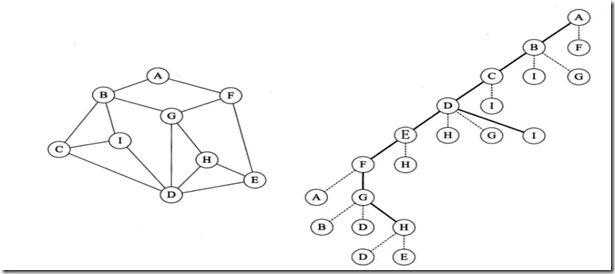
在上图中我们坚持沿着右手边走，如果碰见标记的跳过，选择另一条。到最后时再返回遍历确认是否都有标记。其实就是树的前序遍历。以上图为例，假定A是出发点，首先访问A。这时两个邻接点B、F均未被访问，右手边为B，访问B之后，按照右手原则遍历到C，相同原理A→B→C→D→E→F,在F上向右为A，因为A遍历过，则访问G。最后到H，再走发现到D,E,两者都访问了。关键此时，还有没访问到的，按照原路返回，返回到G，一条条返回，最后得到的访问序列为A→B→C→D→E→F→G→H→I。

2、代码实现

深度优先遍历，也有称为深度优先搜索，简称DFS。其实，就像是一棵树的前序遍历。

算法思想： 它从图中某个结点v出发，访问此顶点，然后从v的未被访问的邻接点出发深度优先遍历图，直至图中所有和v有路径相通的顶点都被访问到。若图中尚有顶点未被访问，则另选图中一个未曾被访问的顶点作起始点，重复上述过程，直至图中的所有顶点都被访问到为止。

这是类似树的前序遍历算法，所以在程序实现上，很像前序遍历，同时在算法复杂度呈现出不同。

//邻接矩阵的深度递归算法
void  GraphData::DFS(GraphArray *pArray,int i)
{
    int j = 0;
    printf("%c",pArray->vex[i]);   //打印顶点，也可以其他操作
    for (j = 0; j< pArray->numVertexes;j++)
    {
        if (!bVisited[j]&&pArray->arg[i][j] == 1)    //关键之前初始化时，有关系的边赋值为1，所以由此进行判断
        {
            DFS(pArray,j);        //对为访问的邻接顶点递归调用
        }
    }
}
//邻接矩阵的深度遍历操作
void  GraphData::DFSTraverse(GraphArray *pArray)
{
    int i;
    for (i = 0;i < pArray->numVertexes;i++)
    {
        bVisited[i] = false;
    }
    for(i = 0; i< pArray->numVertexes;i++)
    {
        if (!bVisited[i])
        {
            DFS(pArray,i);
        }
    }
}

 

//邻接表的深度递归算法
void GraphData::DFS(GraphList *pList,int i)
{
    EdgeNode *itemNode;
    bVisited[i] = true;
    printf("%c",pList->vertexList[i].nNodeData); //打印顶点数据
    itemNode = pList->vertexList[i].pFirstNode;
    while(itemNode)
    {
        if (!bVisited[itemNode->nNodevex])
        {
            DFS(pList,itemNode->nNodevex);
        }
        itemNode = itemNode->next;
    }
}
//邻接表的深度遍历操作
void  GraphData::DFSTraverse(GraphList* pList)
{
    int i;
    GraphList *pGraphList = pList;
    for ( i = 0;pGraphList->numVertess;i++)
    {
        bVisited[i] = false;
    }
    for (i = 0;i < pGraphList->numVertess;i++)
    {
        if (!bVisited[i])
        {
            DFS(pGraphList,i);
        }        
    }
}

对比两个不同的存储结构的深度优先遍历算法，对于n个顶点e条边的图来说，邻接矩阵由于是二维数组，要查找某个顶点的邻接点需要访问矩阵中的所有元素，因为需要O(n²)的时间。而邻接表做存储结构时，找邻接点所需的时间取决于顶点和边的数量，所以是O(n+e)。显然对于点多边少的稀疏图来说，邻接表结构使得算法在时间效率上大大提高。

三、广度优先搜索遍历

1、原理

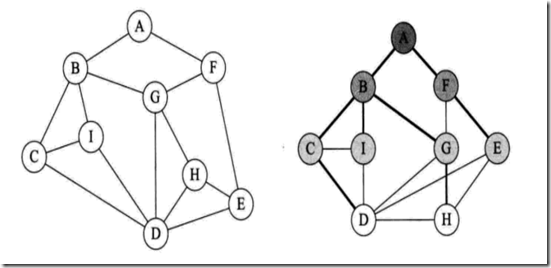
图的广度优先遍历算法是一个分层遍历的过程，和二叉树的广度优先遍历类似，其基本思想在于：从图中的某一个顶点Vi触发，访问此顶点后，依次访问Vi的各个为层访问过的邻接点，然后分别从这些邻接点出发，直至图中所有顶点都被访问到。广度优先遍历类似树的层序遍历。

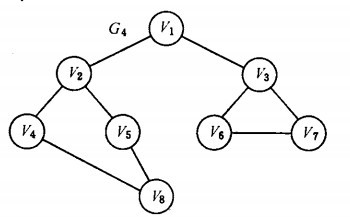
首先访问v1 和v1 的邻接点v2 和v3，然后依次访问v2 的邻接点v4 和v5 及v3 的邻接点v6 和v7，最后访问v4 的邻接点v8。由于这些顶点的邻接点均已被访问，并且图中所有顶点都被访问，由些完成了图的遍历。得到的顶点访问序列为：

v1→v2 →v3 →v4→ v5→ v6→ v7 →v8

和深度优先搜索类似，在遍历的过程中也需要一个访问标志数组。并且，为了顺次访问路径长度为2、3、…的顶点，需附设队列以存储已被访问的路径长度为1、2、… 的顶点。

//邻接矩阵的广度遍历操作
void GraphData::BFSTraverse(GraphArray *pArray)
{
    queue<int> itemQueue;
    int i,j;
    for(i = 0 ;i< pArray->numVertexes;i++)
    {
        bVisited[i] = false;
    }
    for(i = 0;i< pArray->numVertexes;i++)//每个顶点循环
    {
        if (!bVisited[i])//访问未被访问的顶点
        {
            bVisited[i] = true;
            printf("%c",pArray->vex[i]);
            itemQueue.push(i);   //将此结点入队
            while(!itemQueue.empty())
            {
                int m = itemQueue.front();   //结点出队
                itemQueue.pop();
                for(j = 0;j< pArray->numVertexes;j++)
                {
                    //判断其他顶点与当前顶点存在边且未被访问过。
                    if (!bVisited[j] && pArray->arg[m][j] == 1)
                    {
                        bVisited[j] = true;
                        printf("%c",pArray->vex[j]);
                        itemQueue.push(j);
                    }
                }
            }
        }
    }
}
//邻接表的广度遍历操作
void GraphData::BFSTraverse(GraphList *pList)
{
    queue<int> itemQueue;
    int i,j;
    EdgeNode* pitemNode;
    for(i = 0 ;i< pList->numVertess;i++)
    {
        bVisited[i] = false;
    }
    for(i = 0;i<pList->numVertess;i++)
    {
        if (!bVisited[i])
        {
            bVisited[i] = true;
            printf("%c",pList->vertexList[i].nNodeData);
            itemQueue.push(i);
            while(!itemQueue.empty())
            {
                int m = itemQueue.front();
                itemQueue.pop();
                pitemNode = pList->vertexList[m].pFirstNode;
                while(pitemNode)
                {
                    if (bVisited[pitemNode->nNodevex])
                    {
                        bVisited[pitemNode->nNodevex] = true;
                        printf("%c",pList->vertexList[pitemNode->nNodevex].nNodeData);
                        itemQueue.push(pitemNode->nNodevex);
                    }
                    pitemNode = pitemNode->next;
                }

            }
        }
    }
}

总结：对比图的深度优先遍历与广度优先遍历算法，会发现，它们在时间复杂度上是一样的，不同之处仅仅在于对顶点的访问顺序不同。可见两者在全图遍历上是没有优劣之分的，只是不同的情况选择不同的算法。