Huffman树及其应用

哈夫曼树又称为最优二叉树，哈夫曼树的一个最主要的应用就是哈夫曼编码，本文通过简单的问题举例阐释哈夫曼编码的由来，并用哈夫曼树的方法构造哈夫曼编码，最终解决问题来更好的认识哈夫曼树的应用--哈夫曼编码。

一、引子

在学习中我们经常遇到将各科成绩改为优秀、良好、中等、及格和不及格。那么根据分级原理，代码表示为：

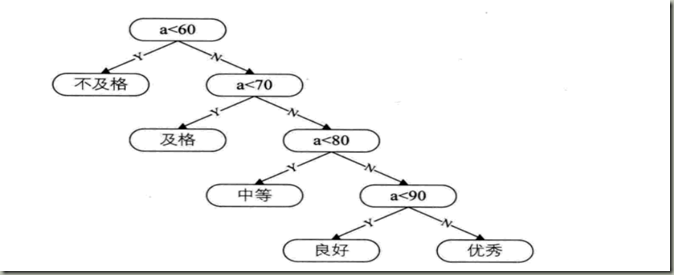
if(a<60)
   b = "不及格“;
else if(a<70)
  b = "及格";
else if(a<80)
  b = "中等";
else if(a<90)
  b = "良好";
else if(a<70)
  b = "优秀";

那么用二叉树表示为：

在实际应用中，5个学生等级的分布规律如表所示

分数	0~59	60~ 69	70~79	80~89	90~100
所占比例	5%	15%	40%	30%	10%

在上面中70分以上的比例是80%，但都需要经过三次比较判断才得出结果，显然不合理。

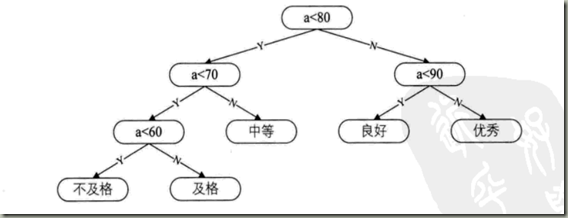
Huffman提出了想法，加入修改成如图所示

二、Huffman定义和原理

根据上面例子的引出，我们将各个成绩所占比例，当做权重标示在分支上，如图所示

哈夫曼树定义为：给定n个权值作为n个叶子结点，构造出的一棵二叉树带权路径长度达到最小。

1、路径和路径长度

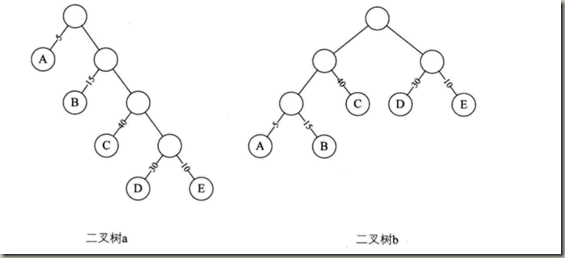
在一棵树中，从一个结点往下可以达到的孩子或子孙结点之间的通路，称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1，则从根结点到第L层结点的路径长度为L-1。在二叉树a中根节点到结点D路径长度为4，在二叉树b中结点D到根节点路径长度为2.

树的路径长度：树根到每个结点的路径长度之和。二叉树a = 1+1+2+2+3+3+4+4= 20.二叉树B = 1+2+3+3+2+1+2+2 = 16.

2、结点的权及带权路径长度

若将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权。结点的带权路径长度为：从根结点到该结点之间的路径长度与该结点的权的乘积。

3、树的带权路径长度

树的带权路径长度规定为所有叶子结点的带权路径长度之和。

树的带权路径长度计算

二叉树a = 5*1+15*2+40*3+30*4+10*4 = 315；

二叉树b = 5*3+15*3+40*2+30*2+10*2 = 220；

如果我们现在用10000个学生需要转换，二叉树a需要31500（别往里是百分数，315/100*10000),二叉树b需要22000次，差不多少了三分之一呢。

从定义中可以看出哈夫曼树的一个最重要的特点：带权路径长度最短。

huffman树构建

哈夫曼编码步骤：

一、对给定的n个权值{W1,W2,W3,...,Wi,...,Wn}构成n棵二叉树的初始集合F= {T1,T2,T3,...,Ti,...,Tn}，其中每棵二叉树Ti中只有一个权值为Wi的根结点，它的左右子树均为空。（为方便在计算机上实现算法，一般还要求以Ti的权值Wi的升序排列。）
二、在F中选取两棵根结点权值最小的树作为新构造的二叉树的左右子树，新二叉树的根结点的权值为其左右子树的根结点的权值之和。
三、从F中删除这两棵树，并把这棵新的二叉树同样以升序排列加入到集合F中。
四、重复二和三两步，直到集合F中只有一棵二叉树为止。

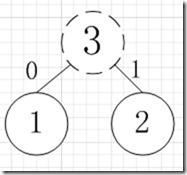
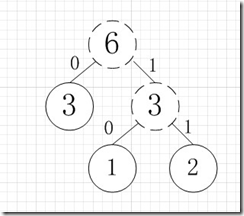
简易的理解就是，假如我有A,B,C,D,E五个字符，出现的频率（即权值）分别为5,4,3,2,1,那么我们第一步先取两个最小权值作为左右子树构造一个新树，即取1，2构成新树，其结点为1+2=3，如图：

虚线为新生成的结点，第二步再把新生成的权值为3的结点放到剩下的集合中，所以集合变成{5,4,3,3}，再根据第二步，取最小的两个权值构成新树，如图：

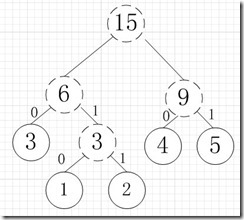
再依次建立哈夫曼树，如下图：

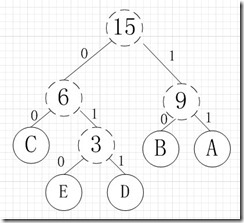
其中各个权值替换对应的字符即为下图：

所以各字符对应的编码为：A->11,B->10,C->00,D->011,E->010

//在Huffman结点数组中找权值最小的两个结点i1和i2
void SelectNode(pHuffmanNode itemnode,int &MinNum1,int &MinNum2,int num)
{
    /* 假设两个结点的权值 */
    int MaxWeight1,MaxWeight2;
    MaxWeight1 = MaxWeight2 = 10000;
    /* 找出所有结点中权值最小、无父结点的两个结点*/
    for(int i = 0;i<num;i++)
    {
        //parent不为-1，就是已经判断过了。
        if (itemnode[i].weight<MaxWeight1&&itemnode[i].parent == -1)
        {
            //将m1赋值给m2保证m1是最小的，m2是第二小的
            MaxWeight2 = MaxWeight1;
            MinNum2 = MinNum1;
            MaxWeight1 = itemnode[i].weight;
            MinNum1 = i;
        }
        else if (itemnode[i].weight<MaxWeight2&& itemnode[i].parent == -1)
        {
            MaxWeight2 = itemnode[i].weight;
            MinNum2     = i;
        }
    }
}

//创建huffman树
void CreateHuffman(pHuffmanNode HuffmanNodeArray,int n)
{    
    //创建树结点
    //叶子结点（度为0)的个数为n，分支结点（度为2的n2)是n-1，二叉树没有n1，所以树结点为2*n-1;
    for (int i = 0;i< 2*n-1;i++)
    {
        HuffmanNodeArray[i].weight =0;
        HuffmanNodeArray[i].parent = -1;
        HuffmanNodeArray[i].lchild = -1;
        HuffmanNodeArray[i].rchild = -1;
        HuffmanNodeArray[i].value = i;

    }

    //创建权值的结点，也就是在HUffman中叶子结点
    for (int i = 0;i<n;i++)
    {
        cout<<"Please input weight of leaf node"<<endl;
        cin>>HuffmanNodeArray[i].weight;
    }

    //循环构建Huffman树，需要判断n-1次
    for (int i = n;i<2*n-1;i++)
    {
        int minNum1 = 0;
        int minNum2 = 0;
        SelectNode(HuffmanNodeArray,minNum1,minNum2,i);
        //minNum1,minNum2数值小于n，其实就是为叶子结点确定父节点是谁。
        HuffmanNodeArray[minNum1].parent = i;
        HuffmanNodeArray[minNum2].parent = i;
        //创建两个叶子结点的父节点（分支结点），确定左右孩子，赋值权重
        HuffmanNodeArray[i].weight = HuffmanNodeArray[minNum1].weight+HuffmanNodeArray[minNum2].weight;
        HuffmanNodeArray[i].rchild = minNum1;
        HuffmanNodeArray[i].lchild = minNum2;

    }    
    
}

CreateHuffman

Huffman编码

赫夫曼在研究这种最优二叉树时的主要目的是解决当年远距离通信（主要是电报）的数据传输的最优化问题。比如传输一串字符“BADCADFEED”，采用二进制数据表示，如下表：

字母	A	B	C	D	E	F
二进制字符	000	001	010	011	100	101

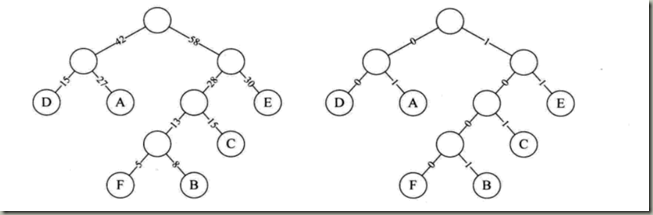
编码之后的二进制数据流为“001000011010000011101100100011”，对方接收时同样按照3位一组解码。现在假设这6个字母出现的频率不同，A 27%，B %8，C 15%，D 15%，E 30%，F 5%。下面将27、8、15、15、30、5分别作为A、B、C、D、E、F的权值构造赫夫曼树，如下图：

将右图赫夫曼树的权值左分支改为0，右分支改为1。

现在将这6个字母用从根节点到叶子所经过路径的0或1来编码，得到的编码表如下：

字母	A	B	C	D	E	F
编码	01	1001	101	00	11	1000

将“BADCADFEED”再次编码得到“1001010010101001000111100”，共25个字符，与之前编码得到的30个字符相比大约节约了17%的存储和传输成本。

在解码时，用同样的赫夫曼树，即发送方和接收方约定好同样的赫夫曼编码规则。当接收方接收到“1001010010101001000111100”时，比对右图中的赫夫曼树。

void CreateHuffmanCode(pHuffmanNode itemHuffmanNode,pHuffmanCode itemHuffmanCode,int n)
{
    //获取huffman树，从叶子结点开始遍历，现找到叶子结点的父节点，如果此节点在左边就是0，否则就是1
    int ntemp,ptemp;
    HuffmanCode phutemp;
    for (int i = 0;i<n;i++)
    {
         ntemp = i;
        phutemp.start = n-1;
        ptemp = itemHuffmanNode[i].parent;
        //循环这个叶子结点的父节点，当父节点为-1是，就是到了树的根节点
        while(ptemp != -1)
        {
            if (itemHuffmanNode[ptemp].lchild == ntemp)
            {
                phutemp.Bit[phutemp.start] = 0;
            }
            else
                phutemp.Bit[phutemp.start] = 1;
            phutemp.start--;
            ntemp = ptemp;
            ptemp = itemHuffmanNode[ntemp].parent;
        }

        /* 保存求出的每个叶结点的哈夫曼编码和编码的起始位 */
        for (int j=phutemp.start+1; j<n; j++)
        { itemHuffmanCode[i].Bit[j] = phutemp.Bit[j];}
        itemHuffmanCode[i].start = phutemp.start;
    }
}

CreateDecode

代码

  1 #include <iostream>
  2 #include <stdio.h>
  3 using namespace std;
  4 
  5 const int MAXBIT = 100;
  6 const int MAXVALUE = 1000;
  7 //创建结构体，抽象描述树节点
  8 typedef struct HuffmanNode
  9 {
 10     int parent;
 11     int lchild;
 12     int rchild;
 13     //结点权重
 14     int weight;
 15     //可以写字母等其他雷兴国
 16     int value;
 17 }stu_HuffmanNode,*pHuffmanNode;
 18 //创建结构体，保存编码
 19 typedef struct HuffmanCode
 20 {
 21     //编码的bit
 22     int Bit[MAXBIT];
 23     int start;
 24 }*pHuffmanCode;
 25 
 26 //在Huffman结点数组中找权值最小的两个结点i1和i2
 27 void SelectNode(pHuffmanNode itemnode,int &MinNum1,int &MinNum2,int num)
 28 {
 29     /* 假设两个结点的权值 */
 30     int MaxWeight1,MaxWeight2;
 31     MaxWeight1 = MaxWeight2 = 10000;
 32     /* 找出所有结点中权值最小、无父结点的两个结点*/
 33     for(int i = 0;i<num;i++)
 34     {
 35         //parent不为-1，就是已经判断过了。
 36         if (itemnode[i].weight<MaxWeight1&&itemnode[i].parent == -1)
 37         {
 38             //将m1赋值给m2保证m1是最小的，m2是第二小的
 39             MaxWeight2 = MaxWeight1;
 40             MinNum2 = MinNum1;
 41             MaxWeight1 = itemnode[i].weight;
 42             MinNum1 = i;
 43         }
 44         else if (itemnode[i].weight<MaxWeight2&& itemnode[i].parent == -1)
 45         {
 46             MaxWeight2 = itemnode[i].weight;
 47             MinNum2     = i;
 48         }
 49     }
 50 }
 51 
 52 //创建huffman树
 53 void CreateHuffman(pHuffmanNode HuffmanNodeArray,int n)
 54 {    
 55     //创建树结点
 56     //叶子结点（度为0)的个数为n，分支结点（度为2的n2)是n-1，二叉树没有n1，所以树结点为2*n-1;
 57     for (int i = 0;i< 2*n-1;i++)
 58     {
 59         HuffmanNodeArray[i].weight =0;
 60         HuffmanNodeArray[i].parent = -1;
 61         HuffmanNodeArray[i].lchild = -1;
 62         HuffmanNodeArray[i].rchild = -1;
 63         HuffmanNodeArray[i].value = i;
 64 
 65     }
 66 
 67     //创建权值的结点，也就是在HUffman中叶子结点
 68     for (int i = 0;i<n;i++)
 69     {
 70         cout<<"Please input weight of leaf node"<<endl;
 71         cin>>HuffmanNodeArray[i].weight;
 72     }
 73 
 74     //循环构建Huffman树，需要判断n-1次
 75     for (int i = n;i<2*n-1;i++)
 76     {
 77         int minNum1 = 0;
 78         int minNum2 = 0;
 79         SelectNode(HuffmanNodeArray,minNum1,minNum2,i);
 80         //minNum1,minNum2数值小于n，其实就是为叶子结点确定父节点是谁。
 81         HuffmanNodeArray[minNum1].parent = i;
 82         HuffmanNodeArray[minNum2].parent = i;
 83         //创建两个叶子结点的父节点（分支结点），确定左右孩子，赋值权重
 84         HuffmanNodeArray[i].weight = HuffmanNodeArray[minNum1].weight+HuffmanNodeArray[minNum2].weight;
 85         HuffmanNodeArray[i].rchild = minNum1;
 86         HuffmanNodeArray[i].lchild = minNum2;
 87 
 88     }    
 89     
 90 }
 91 
 92 void CreateHuffmanCode(pHuffmanNode itemHuffmanNode,pHuffmanCode itemHuffmanCode,int n)
 93 {
 94     //获取huffman树，从叶子结点开始遍历，现找到叶子结点的父节点，如果此节点在左边就是0，否则就是1
 95     int ntemp,ptemp;
 96     HuffmanCode phutemp;
 97     for (int i = 0;i<n;i++)
 98     {
 99          ntemp = i;
100         phutemp.start = n-1;
101         ptemp = itemHuffmanNode[i].parent;
102         //循环这个叶子结点的父节点，当父节点为-1是，就是到了树的根节点
103         while(ptemp != -1)
104         {
105             if (itemHuffmanNode[ptemp].lchild == ntemp)
106             {
107                 phutemp.Bit[phutemp.start] = 0;
108             }
109             else
110                 phutemp.Bit[phutemp.start] = 1;
111             phutemp.start--;
112             ntemp = ptemp;
113             ptemp = itemHuffmanNode[ntemp].parent;
114         }
115 
116         /* 保存求出的每个叶结点的哈夫曼编码和编码的起始位 */
117         for (int j=phutemp.start+1; j<n; j++)
118         { itemHuffmanCode[i].Bit[j] = phutemp.Bit[j];}
119         itemHuffmanCode[i].start = phutemp.start;
120     }
121 }
122 
123 //解码
124 void decodeHuffman(char* str ,pHuffmanNode itemHuffmanNode,int Num)
125 {
126     int i,tmp=0,code[1024];
127     int m=2*Num-1;
128     char *nump;
129     char num[1024];
130     //将权值设置为0,1
131     for(i=0;i<strlen(str);i++)
132     {
133         if(str[i]=='0')
134             num[i]=0;        
135         else
136             num[i]=1;                    
137     } 
138     i = 0;
139     nump = &num[0];
140     while(nump < (&num[strlen(str)]))
141     {
142         tmp = m-1;
143         //循环获取叶子结点在数组中序号
144         while(itemHuffmanNode[tmp].lchild != -1&& itemHuffmanNode[tmp].rchild != -1)
145         {
146             if (*nump == 0)
147             {
148                 tmp = itemHuffmanNode[tmp].lchild;
149             }
150             else
151                 tmp = itemHuffmanNode[tmp].rchild;
152             nump++;
153         }
154     }
155     cout<<itemHuffmanNode[tmp].value<<endl;
156 }
157 
158 int main()
159 {
160     HuffmanNode HuffmanNodeArray[100];
161     HuffmanCode HuffmanCodeArray[100];
162     pHuffmanNode phuffman= &HuffmanNodeArray[0];
163     pHuffmanCode phuffmancode = &HuffmanCodeArray[0];
164     cout<<"输入个数"<<endl;
165     int n ;
166     cin>>n;
167     CreateHuffman(phuffman,n);
168     CreateHuffmanCode(phuffman,phuffmancode,n);
169     for (int i = 0;i< n;i++)
170     {
171         cout<<phuffmancode[i].start<<endl;
172     }
173     cout<<"输入解码符号"<<endl;
174     int test;
175     cin>>test;
176     decodeHuffman("test",phuffman,n);
177     system("pause");
178 }

HuffmanTest

posted @ 2015-08-19 15:04 bldong 阅读(1927) 评论(0) 编辑收藏举报

刷新页面返回顶部

不归路

没有坚持，何谈梦想

Huffman树及其应用

一、引子

二、Huffman定义和原理

huffman树构建

Huffman编码

代码

公告