浅谈数据结构系列 栈和队列

计算机程序离不开算法和数据结构,在数据结构算法应用中，栈和队列应用你比较广泛，因为两者在数据存放和读取方面效率比较高，本章节重点讲解两者的基本概念和实现。

基本概念

栈：是一种先进后出，后进先出的数据结构，本质上是线性表，只是限制仅允许在表的一段进行插入和删除工作。此端为栈顶，这是在栈中应用很关键的概念。所有数据的处理都是在栈顶进行的，进栈时，栈中元素增加，栈顶上移一位，出栈时栈顶下移一位。应用中比如：洗碗，每次洗干净的碗放在上面-进栈，取碗，从顶上取出一个-出栈；装子弹-进栈，开枪-出栈。

队列：是一种先进先出的数据结构，同样是线性表，允许在表一段进行插入（队尾），而表的另一端进行删除工作（队头）。应用中比如：购物-先到的先购物，晚到的在队尾后买物品。

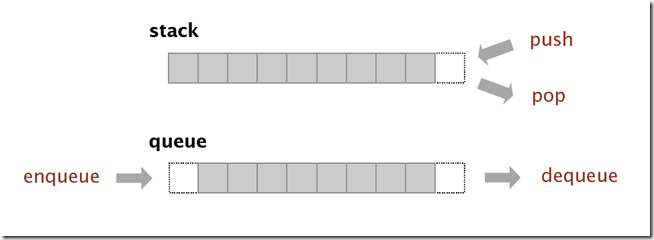
存储结构

因为在c++中已经有实现的stack和queue，我们就以程序中封装的程序进行解读。

1、顺序存储结构

数组本质上是顺序存储结构，所以在栈和队列的顺序存储结构上的实现，用数组实现即可，也就是在数组基础上进行二次封装，也就意味着会有溢出的现象。

a.栈的顺序存储结构

：push，直接添加一个元素s[n]到数组，pop直接返回s[n-1]

template<typename T>
class MyStack
{
     T item[] ;
     int number;
     int Max;
    MyStack()
    {
        Max= 20;
        item = T[20];
        number = 0;
    }
    //入栈
    void MyStack::Push(T _item)
    {
        //如果超过数组大小，则重新申请控件
        if (number == Max) Resize(2 * Max);
        //number记录数组中个数，同时将push的元素放在数组最后面。先赋值然后number++.
        item[number++] = _item;
    }
    //出栈
     T MyStack::Pop()
    {
        //先——再获取元素.
        T temp = item[--number];
        //其他设置为kong
        item[number] = default(T);
        if (number > 0 && number == Max / 4) Resize(Max / 2);
        return temp;
    }

     void MyStack::Resize(int capacity)
    {
        T[] temp = new T[capacity];
        for (int i = 0; i < Max; i++)
        {
            temp[i] = item[i];
        }
        item = temp;
    }
};

 

当我们缩小数组的时候，采用的是判断1/4的情况，这样效率要比1/2要高，因为可以有效避免在1/2附件插入，删除，插入，删除，从而频繁的扩大和缩小数组的情况。

特点

1. Pop和Push操作在最坏的情况下与元素个数成比例的N的时间，时间主要花费在扩大或者缩小数组的个数时，数组拷贝上。

2. 元素在内存中分布紧凑，密度高，便于利用内存的时间和空间局部性，便于CPU进行缓存，较LinkList内存占用小，效率高。

b.队列的顺序存储结构

队列中也是用数组进行实现，但是在队列中需要用dead和tail来记录头元素和尾元素。在这一段连续的存储空间中，由一个队列头指针和一个尾指针表示这个队列，当头指针和尾指针指向同一个位置时，队列为空，也就是说，队列是由两个指针中间的元素构成的。当出队操作时，头指针向前(即向量空间的尾部)增加一个位置，入队时，尾指针向前增加一个位置。

队列是空还是满。方法至少有三种，一种是另设一个布尔变量来判断(就是请别人看着，是空还是满由他说了算)，第二种是少用一个元素空间，当入队时，先测试入队后尾指针是不是会等于头指针，如果相等就算队已满，不许入队。第三种就是用一个计数器记录队列中的元素的总数，这样就可以随时知道队列的长度了，只要队列中的元素个数等于向量空间的长度，就是队满。

#define OVERFLOW -2   
#define QUEUEEMPTY  -3 
template<typename T>
class ArrayQueue
{
    T item[];
    int Max;
    int front ;
    int rear;
 ArrayQueue()
 {
     Max = 20;
     item = T[20];
     front = 0;
     rear = 0;
 }
 //入栈
 void ArrayQueue::Push(T _item)
 {
     //如果超过数组大小，则重新申请空间
     if ((rear++ % Max) == front) exit(OVERFLOW);
     //形成循环队列,当超过rear超过max用取余数方式重新计算.
     rear = (rear +1)%Max;
     item[rear++] = _item;
 }
 //出栈
 T ArrayQueue::Pop()
 {
     //先——再获取元素.
     if (QueueEmpty())
     {
         exit(QUEUEEMPTY)
     }
     front = (front+1)%Max;
     T temp = item[front];     
     return temp;
 }
 /************************************************************************/  
 /*    判断队列Q是否为空                                                              
 */  
 /************************************************************************/  
 int QueueEmpty()  
 {  
     if(front==rear) return TRUE;  
     else return FALSE;  
 } 
};

 

区别：在栈顺序存储结构比较简单，直接用数组标示获取即可，在队列中需要考虑循环队列的问题。在队列实现中rear和front都是++，所以总会溢出的现象，通过取余的处理，实现循环队列，很有意思，很有价值。

2、链式存储结构

a.栈的链表实现

若是栈中元素的数目变化范围较大或不清楚栈元素的数目，就应该考虑使用链式存储结构。人们将用链式存储结构表示的栈称作"链栈"。

push：向栈顶压入一个元素，首先保存原先的位于栈顶的元素，然后新建一个新的栈顶元素，然后将该元素的下一个指向原先的栈顶元素。

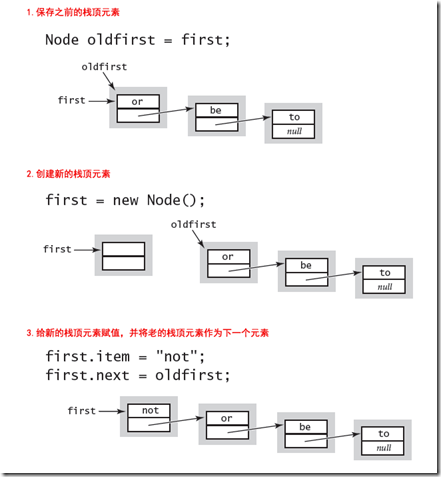
pop 首先保存栈顶元素的值，然后将栈顶元素设置为下一个元素

class ListStack
{
public:
    typedef struct LNode{    
        int        data;                 
        struct LNode   *next;       
    }LNode, *LinkList;  

    LinkList phead,current;
    ListStack()
    {
        //链表的创建        
        
         phead= new LNode();
        phead->data = 0;
        phead->next = NULL;        
        
    }
    /************************************************************************/  
    /* 入栈  
    */  
    /************************************************************************/  
    void ListStack::Push(int data)  
    {  
        LinkList p;  
        p = (LinkList )malloc(sizeof(LNode));  
        if (!p) exit(OVERFLOW);  
        //其实就是单链表的插入工作,采用的是头插法，新插入的在最上端
        p->data = data;  
        p->next = phead->next;
        phead->next = p;          
    }  


    /************************************************************************/  
    /* 出栈 
    */  
    /************************************************************************/  
    void ListStack::Pop()  
    {  
        //由于是头插法，直接删除，获取即可
        LinkList p;  
        if(StackEmpty()) return;           
        p = phead->next;
        phead->next = p->next;          
        free(p);  
    }  
    /************************************************************************/  
    /* 获取栈顶元素内容 
    */  
    /************************************************************************/  
    int ListStack::GetTop()  
    {  
        if(StackEmpty()) return -1;  
        return phead->next->data;  
    }  

    /************************************************************************/  
    /* 判断栈S是否空  
    */  
    /************************************************************************/  
    int ListStack::StackEmpty()   
    {  
        if(phead==NULL||phead->next == NULL) return 1;  
        return   0;  
    }  
};

 

b 队列的链表实现

上面讨论了栈的链表实现，其中关键点是在进行插入工作时，采用了头插法，实现的栈链表应用，当数据的插入工作在链表的尾端时，则就是队列中链表的实现，也就是获取链表的长度，然后在指定长度下加入元素，完成元素的插入工作。

void ListStack::QueuePush(int data)
    {
        LinkList p,item;  
        p = (LinkList )malloc(sizeof(LNode));  
        if (!p) exit(OVERFLOW);
        if (length>0)
        {
            item = (LinkList)malloc(sizeof(LNode));
           //注意赋值
            item = phead;
            for (int i = 0;i< length&&item->next!= NULL;i++)
            {
                item = item->next;
            }
            p->data = data;
            p->next = item->next;
            item->next = p;
            length++;
        }
        else
        {
            p->data = data;
            p->next = phead->next;
            phead->next = p;
            length++;
        }
        
        
        
    }

 

上面的我关键点就是在链表的我尾部进行元素插入，相对来讲有个遍历的过程。

其他功能函数还是一样的