算法复杂度
1 前言
算法时间复杂度,也就是算法的时间量度,就是在计算机上执行耗时。个算法花费的时间与算法中语句的执行次数成正比例,哪个算法中语句执行次数多,它花费时间就多。在应用中用O表示。
一个算法是由控制结构和原操作构成的,其执行的时间取决于二者的综合效果。为了便于比较同一问题的不同算法,通常把算法中基本操作重复执行的次数(频度)作为算法的时间复杂度。
时间复杂度计算
- 计算复杂度原则
1.去掉运行时间中的所有加法常数。
2.只保留最高阶项。
3.如果最高阶项存在且不是1,去掉与这个最高阶相乘的常数得到时间复杂度
最简单的描述就是找到其中最高次项即可。
举例:
for (int i = 0; i < n; i++) { for (int j = i; j < n; j++) { // do ..... } }
当 i = 0 时 里面的fo循环执行了n次,当i等待1时里面的for循环执行了n - 1次,当i 等于2里里面的fro执行了n - 2次……..所以执行的次数是:
根据我们上边的时间复杂度算法
1.去掉运行时间中的所有加法常数: 没有加法常数不用考虑
2.只保留最高阶项: 只保留 
- 去掉与这个最高阶相乘的常数: 去掉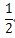 只剩下
只剩下 
最终这个算法的时间复杂度为
- 常数阶:一个算法没有循环语句,则算法中基本操作的执行频度与问题规模n无关,记作O(1)
Temp=i;i=j;j=temp;以上三条单个语句的频度均为1,该程序段的执行时间是一个与问题规模n无关的常数。算法的时间复杂度为常数阶,记作T(n)=O(1)。如果算法的执行时 间不随着问题规模n的增加而增长,即使算法中有上千条语句,其执行时间也不过是一个较大的常数。此类算法的时间复杂度是O(1)。就是和N没有关系。
- 线性阶:如果算法只有一个一重循环,则算法的基本操作的执行频度与问题规模n呈线性增大关系,记作O(n)。
a=0; b=1; ① for (i=1;i<=n;i++) ② { s=a+b; ③ b=a; ④ a=s; ⑤ }
解: 语句1的频度:2,
语句2的频度: n,
语句3的频度: n-1,
语句4的频度:n-1,
语句5的频度:n-1,
T(n)=2+n+3(n-1)=4n-1=O(n).
- 对数阶
i=1; ① while (i<=n) i=i*2; ②
解: 语句1的频度是1,
设语句2的频度是f(n), 则:2^f(n)<=n;f(n)<=log2n
取最大值f(n)= log2n,
T(n)=O(log2n )
- 平方阶
//交换i和j的内容 sum=0; // (一次) for(i=1;i<=n;i++) // (n次 ) for(j=1;j<=n;j++) //(n^2次 ) sum++; //(n^2次 ) //解:T(n)=2n^2+n+1 =O(n^2) for (i=1;i { y=y+1; ① for (j=0;j<=(2*n);j++) x++; ② }
解: 语句1的频度是n-1
语句2的频度是(n-1)*(2n+1)=2n^2-n-1
f(n)=2n^2-n-1+(n-1)=2n^2-2
该程序的时间复杂度T(n)=O(n^2).
- 立方阶
for(i=0;i { for(j=0;j { for(k=0;k x=x+2; } }
解:当i=m, j=k的时候,内层循环的次数为k当i=m时, j 可以取 0,1,…,m-1 , 所以这里最内循环共进行了0+1+…+m-1=(m-1)m/2次所以,i从0取到n, 则循环共进行了: 0+(1-1)*1/2+…+(n-1)n/2=n(n+1)(n-1)/6所以时间复杂度为O(n^3).

综述
最坏情况运行时间是一种保证,就是运行时间不能再坏了。在应用中,我们提到的运行时间一般是最坏情况的运行时间。平均运行时间是所有情况中最有意义的,因为它是期望的运行时间。
对算法的分析一是平均时间复杂度,还有就是最坏时间复杂度,没有特殊情况下就是指最坏时间复杂度。
我们还应该区分算法的最坏情况的行为和期望行为。如快速排序的最 坏情况运行时间是 O(n^2),但期望时间是 O(nlogn)。通过每次都仔细 地选择基准值,我们有可能把平方情况 (即O(n^2)情况)的概率减小到几乎等于 0。在实际中,精心实现的快速排序一般都能以 (O(nlogn)时间运行。
访问数组中的元素是常数时间操作,或说O(1)操作。一个算法如 果能在每个步骤去掉一半数据元素,如二分检索,通常它就取 O(logn)时间。用strcmp比较两个具有n个字符的串需要O(n)时间 。常规的矩阵乘算法是O(n^3),因为算出每个元素都需要将n对 元素相乘并加到一起,所有元素的个数是n^2。
指数时间算法通常来源于需要求出所有可能结果。例如,n个元 素的集合共有2n个子集,所以要求出所有子集的算法将是O(2n)的 。指数算法一般说来是太复杂了,除非n的值非常小,因为,在 这个问题中增加一个元素就导致运行时间加倍。不幸的是,确实有许多问题 (如著名 的“巡回售货员问题” ),到目前为止找到的算法都是指数的。如果我们真的遇到这种情况, 通常应该用寻找近似最佳结果的算法替代之。
版权声明:本文为博主原创文章,未经博主允许不得转载。


