回溯法解决迷宫求解问题

一、迷宫求解问题

如下图小球在起点(1,1)需要移动到终点(6,5),求能否顺利到达终点，若能，路径是什么。

下图即为采用 下->右->上->左的策略得出的结果。

二、解决思路

用二维数组map存放小地图，其中，

• 如果元素为0，则为未走过的空闲节点
• 如果元素为1，则表示为墙
• 如果元素为2，表示可以走
• 如果元素为3，说明走过该路，此路不通

1. 如果该元素为0，假设该点可以走通，则按照下、右、上、左的策略依次判断能否走通，如果可以走通，则继续走，直到走不通为止，然后进行回溯
2. 如果终点为2，说明已经找到路径，终止递归。

三、代码实现

/**
 * @author ymy
 * @date 2020/5/12
 * 迷宫求解问题 的 递归实现
 */
public class MazeSolver {

    public  static void  main(String [] args){
        MazeSolver ms = new MazeSolver();
        ms.test();
    }

    public void test(){
        int rows=8;
        int cols=7;
        int [][] map = new int [rows][cols];//地图
        createMap(rows,cols,map);
        displayArray(map);
        System.out.println("-------");
        getWay(map,1,1);
        displayArray(map);
    }

    /**
     *
     * @param map 地图
     * @param i  起点横坐标
     * @param j  起点纵坐标
     * @return  是否找到得到位置
     *
     * 1.如果小球从起点能找到终点，则证明通路找到
     * 2.约定：当地图(i,j)为0时则没走过，若为1时，表示障碍物，如果为2表示走过
     * 3.若该位置为3，则此路不通。
     * 4.策略尝试顺序，下->右->上->左，若路径不通，则回溯
     */
    public boolean getWay(int [][]map,int i,int j){
        if(map[6][5]==2){
            return true;
        }else if(map[i][j]==0){
            map[i][j]=2;
            if (getWay(map,i+1,j)){
                return true;
            }else if (getWay(map,i,j+1)){
                return  true;
            }else if(getWay(map,i-1,j)){
                return true;
            }else if(getWay(map,i,j-1)){
                return true;
            }else {
                map[i][j]=3;
                return false;
            }
        }else {
            return false;
        }
    }

    public void createMap(int rows,int cols,int [][] map){
    //设置障碍
        for (int i = 0; i <cols; i++) {
            map[0][i]=1;
            map[rows-1][i]=1;
        }
        for(int i =0;i<rows;i++){
            map[i][0]=1;
            map[i][cols-1]=1;
        }
        map[3][1]=1;
        map[3][2]=1;
        map[5][3]=1;
        map[5][4]=1;
        map[5][5]=1;
    }

    public void displayArray(int [][] array){
        for (int[] ints : array) {
            for (int anInt : ints) {
                System.out.print(anInt+" ");
            }
            System.out.println();
        }
    }
}

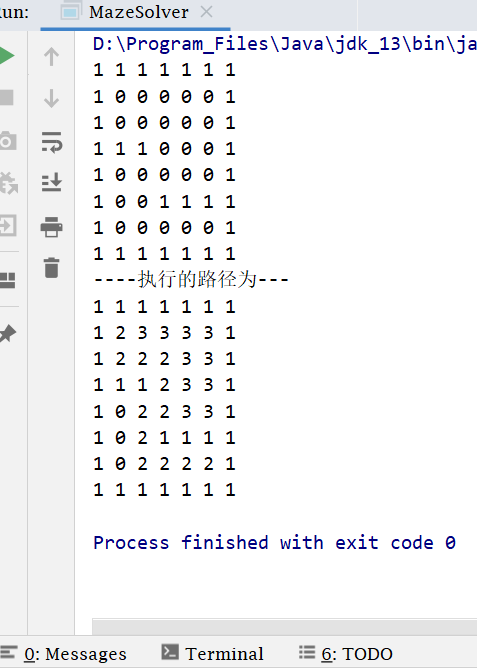
四、测试