BUAA_OO_UNIT1_单元总结
第一单元要求我们构造一个多项式求导器,并通过迭代开发最终实现包含简单幂函数和简单正余弦函数及其嵌套组合函数的导函数的求解。
第一次作业
一、基于度量分析程序结构
UML类图
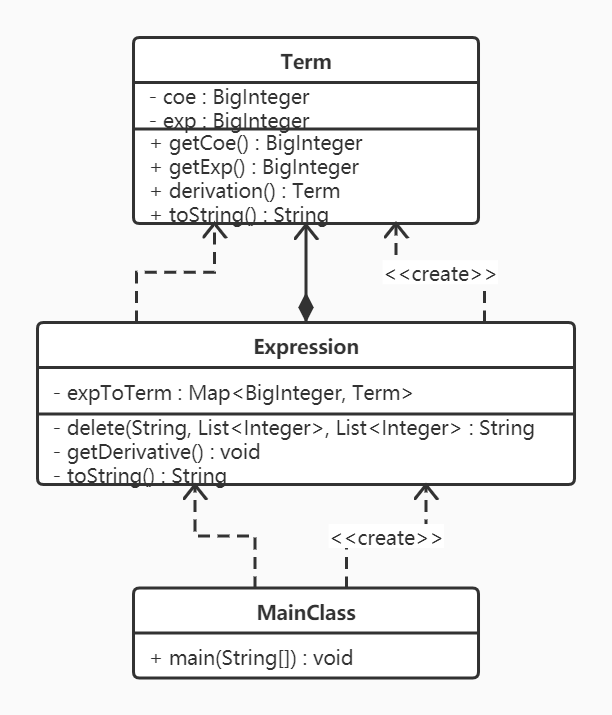
第一次作业的任务为仅包含幂函数的简单多项式的导函数求解。本次任务较为简单,因为表达式中每一项均由乘法运算符连接若干因子组成,总可以化成a*x**b的形式,因此只需根据幂函数的求导法则编写求导函数即可。对于读取到的常数项,其求导结果为0,所以我采用了直接忽视的方法,不进行任何记录与处理。在将表达式逐项分解的过程中,我们可以利用TreeMap将指数相同的项合并以实现最终结果的化简。基于上述考虑,我构造了Term和Expression两个类,分别表示项和表达式,类图如下:
-
Term类:
属性:系数coe、指数exp,均为BigInteger类型
方法:getCoe()、getExp():分别用于获取项的系数、指数
derivation():基于幂函数求导法则实现项的求导
toString():将Term转化为字符串输出,为了达到化简的目的分别考虑系数为0、指数为0、系数为±1、指数为1的情况
-
Expression类:
属性:Map<BigInteger, Term> expToTerm,value为项,key为项的指数
方法:构造方法Expression(String):使用split()分割不同项,每一项中指数相加、系数相乘,如果最终系数不为0,则添加到 expToTerm中
delete(String, List
, List ):辅助分辨每一项中系数与指数的函数 getDerivative():遍历expToTerm,对每一项调用Term类中的derivation()方法
toString():遍历expToTerm,对每一项调用Term类中的toString()方法,中间以"+"连接
-
MainClass类:
由于题目保证输入格式正确,因此在得到输入字符串后便可直接对表达式进行适当简化处理,以便于后续项的分解及求导。处理内容主要包括去掉空白符、合并连续的加减号、将“**”替换为“^”、将省略指数的“*x”替换为“*x^1”、去掉开头的“+”等。经过处理后,表达式不同项之间均以“+”连接,且项内不含“+”,保证之后可以使用“+”来分割不同项。之后实例化Expression类,调用Expression类的getDerivative()、toString()方法完成表达式的求导及结果的输出。
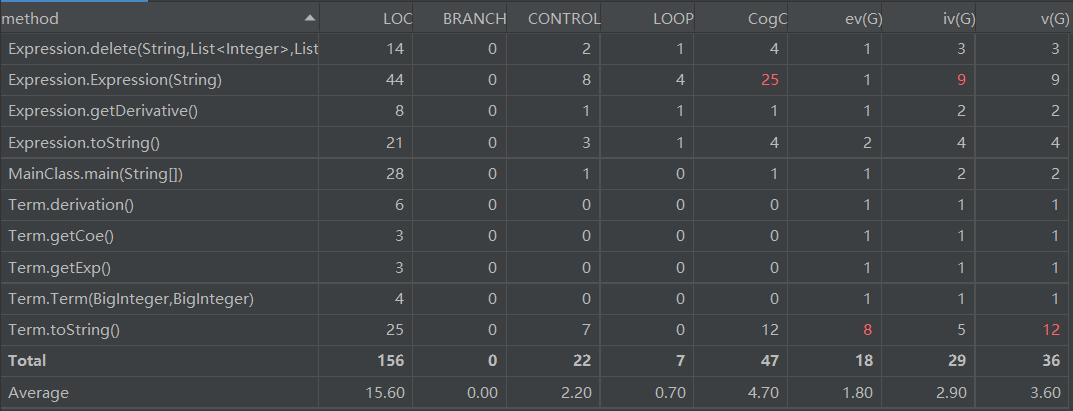
方法复杂度分析
| method | LOC | BRANCH | CONTROL | LOOP | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|---|---|---|---|
| Expression.delete(String,List,List) | 14.0 | 0.0 | 2.0 | 1.0 | 4.0 | 1.0 | 3.0 | 3.0 |
| Expression.Expression(String) | 44.0 | 0.0 | 8.0 | 4.0 | 25.0 | 1.0 | 9.0 | 9.0 |
| Expression.getDerivative() | 8.0 | 0.0 | 1.0 | 1.0 | 1.0 | 1.0 | 2.0 | 2.0 |
| Expression.toString() | 21.0 | 0.0 | 3.0 | 1.0 | 4.0 | 2.0 | 4.0 | 4.0 |
| MainClass.main(String[]) | 28.0 | 0.0 | 1.0 | 0.0 | 1.0 | 1.0 | 2.0 | 2.0 |
| Term.derivation() | 6.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Term.getCoe() | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Term.getExp() | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Term.Term(BigInteger,BigInteger) | 4.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Term.toString() | 25.0 | 0.0 | 7.0 | 0.0 | 12.0 | 8.0 | 5.0 | 12.0 |
| Total | 156.0 | 0.0 | 22.0 | 7.0 | 47.0 | 18.0 | 29.0 | 36.0 |
| Average | 15.6 | 0.0 | 2.2 | 0.7 | 4.7 | 1.8 | 2.9 | 3.6 |
-
度量参数说明:
-
LOC: Lines of code,计算每个方法的代码行数。
-
BRANCH: Number of branch statements,计算每个方法中非结构化分支语句的总数。非结构化分支语句包括switch语句之外的continue语句和break语句。
-
CONTROL: Number of control statements,计算每个方法中控制语句的总数。控制语句包括if、for、while、do、try、break、continue、switch和synchronized语句。
-
LOOP: Number of loop statemrnts,计算每个方法中循环语句的总数,包括for、while和do while。
-
CogC: Cognitive complexity,认知复杂度,用来衡量代码被阅读和理解时的复杂程度。每种控制结构的使用都会增加认知复杂性,而且嵌套的控制结构越多,认知复杂性就越高。
-
ev(G): Essential complexity,基本复杂度,用来衡量程序非结构化程度,ev(G)高意味着非结构化程度高,难以模块化和维护。
-
iv(G): Design complexity,设计复杂度,与方法控制流与对其他方法的调用之间的相互联系有关,也代表了将方法与其调用的方法进行集成所需的最少测试次数。
-
v(G): Cyclomatic Complexity,圈复杂度,是通过每个方法的不同执行路径数量的度量,可以看作是完全执行方法控制流所需的最少测试次数。圈复杂度 = 1+ if、while、for、do、switch cases、catch、条件表达式、&&'和||的数目。
-
-
在Expression类的构造方法Expression()中,控制结构嵌套层数较多,导致认知复杂度和设计复杂度较高。此外,Term类的toString()方法基本复杂度和圈复杂度较高,这主要是因为在判断系数为0、指数为0、系数为±1、指数为1等情况时采用了较多
if-else结构。
类复杂度分析
- 度量参数说明:
- OCavg: Average operation complexity,计算每个类中所有非抽象方法的平均圈复杂度。继承的方法不计算在内。
- OCmax: Maximum operation Complexity,计算每个类中非抽象方法的最大圈复杂度。继承的方法不计算在内。
- WMC: Weighted method complexity,计算每个类中方法的圈复杂度总和。
- 可以看出Expression类的平均操作复杂度较高。
各类代码行数如下:

优缺点分析
优点:设计思路比较清晰,实现较为简单。
缺点:虽然构造了Term和Expression两个类,但Expression类主要用于解析输入的表达式,各种操作带有比较浓重的面向过程色彩,且由于java的标准正则表达式不支持递归,该方法无法处理括号嵌套,导致程序扩展性不高。
二、测试与bug分析
本次作业通过了强测所有数据点,但由于没有考虑到x**2可以优化为x*x,丢失了一部分性能分。
在互测中,我被找到了2类bug。
-
对于设定的形式化表述理解不够深入,没有考虑到三个正负号连在一起的情况,在遇到"+-+"、"-+-"时会出现符号解读上的错误。
修复方法:利用replace()将"+-+"替换为"-","-+-"替换为"+"。
-
在构造expToTerm属性时将指数类型误写为Integer,导致输入项的指数超过integer表示精度时会出现bug。
修复方法:将Integer类型更改为BigInteger类型。
第二次作业
一、基于度量分析程序结构
UML类图
第二次作业的任务为包含简单幂函数和简单正余弦函数的导函数的求解,且出现了由一对括号包裹的表达式因子,存在递归嵌套。由于第一次作业只能处理没有嵌套的简单幂函数,在原有架构上扩展也只能增添三角函数的求导,无法完成递归表达式因子的解析,因此我选择了重构。参考学长编写的四则运算C代码和指导书中的提示,我构建了因子类Factor和运算符类Opeartion,并利用java语言的多态特性,为Operation类创建了两个子类:加法类Add和乘法类Multi。之后在Factor类、Add类和Multi类分别实现了求导接口derivation()。再将输入的整个表达式根据因子类和运算符类构建为二叉树结构,其中叶子节点为Factor,非叶子节点为Operation,最后从根节点出发进行链式求导,输出最终结果即可。
UML类图如下:
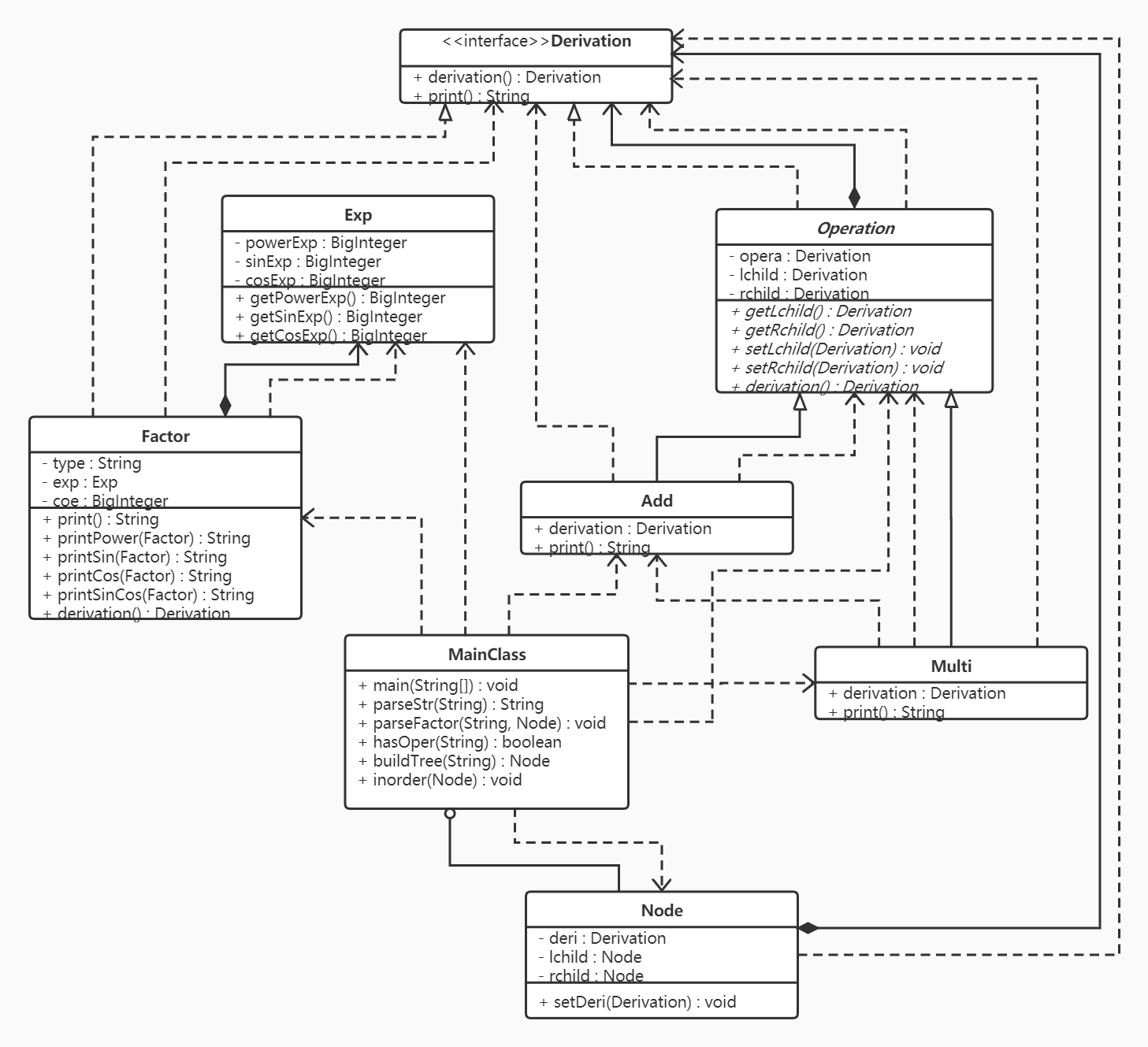
-
求导接口Derivation:
包含抽象方法derivation()和print(),分别用于求导和输出
-
系数类Exp:
属性:幂函数系数powerExp、正弦函数系数sinExp、余弦函数系数cosExp
方法:get类方法
-
因子类Factor:
属性:类型type(包括常数、幂函数、正弦函数、余弦函数、三角函数)、系数exp、指数coe
方法:实现Derivation接口中的求导和输出方法
-
运算符抽象类Operation:
属性:当前节点操作符opera、左孩子lchild、右孩子rchild
方法:get、set类方法
-
加法类Add:继承自Operation类,实现Derivation类的求导和输出方法
-
乘法类Multi:继承自Operation类,实现Derivation类的求导和输出方法
-
-
节点类Node:
属性:当前节点值deri、左孩子lchild、右孩子rchild
方法:setDeri()用于设置当前节点的值
-
主类MainClass:
方法:main(String[]),用于读入表达式并进行简单处理(去空白符、合并正负号等),之后调用buildTree()方法建树,然后对根节点进行递归链式求导,最后从根节点递归输出结果。在此过程中,用到辅助方法hasOper()、parseStr()、parseFactor()、inorder(),功能分别是判断当前表达式是否包含运算符(+或*)、去掉表达式最外层多余括号、解析因子的类型及系数、指数、中序遍历二叉树。
方法复杂度分析
| method | LOC | BRANCH | CONTROL | LOOP | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|---|---|---|---|
| Add.Add() | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Add.Add(Derivation,Derivation) | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Add.derivation() | 4.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Add.print() | 13.0 | 0.0 | 5.0 | 0.0 | 6.0 | 6.0 | 2.0 | 7.0 |
| Exp.Exp(BigInteger,BigInteger,BigInteger) | 5.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Exp.getCosExp() | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Exp.getPowerExp() | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Exp.getSinExp() | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.derivation() | 22.0 | 0.0 | 3.0 | 0.0 | 4.0 | 4.0 | 3.0 | 4.0 |
| Factor.Factor(String,Exp,BigInteger) | 5.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.print() | 8.0 | 0.0 | 5.0 | 0.0 | 5.0 | 6.0 | 5.0 | 6.0 |
| Factor.printCos(Factor) | 10.0 | 0.0 | 5.0 | 0.0 | 7.0 | 6.0 | 4.0 | 8.0 |
| Factor.printPower(Factor) | 10.0 | 0.0 | 5.0 | 0.0 | 7.0 | 6.0 | 4.0 | 8.0 |
| Factor.printSin(Factor) | 10.0 | 0.0 | 5.0 | 0.0 | 7.0 | 6.0 | 4.0 | 8.0 |
| Factor.printSinCos(Factor) | 10.0 | 0.0 | 3.0 | 0.0 | 3.0 | 4.0 | 3.0 | 4.0 |
| MainClass.buildTree(String) | 48.0 | 1.0 | 11.0 | 3.0 | 25.0 | 6.0 | 11.0 | 14.0 |
| MainClass.hasOper(String) | 7.0 | 0.0 | 1.0 | 0.0 | 3.0 | 2.0 | 2.0 | 3.0 |
| MainClass.inorder(Node) | 11.0 | 0.0 | 2.0 | 0.0 | 4.0 | 2.0 | 2.0 | 3.0 |
| MainClass.main(String[]) | 48.0 | 0.0 | 1.0 | 0.0 | 1.0 | 1.0 | 2.0 | 2.0 |
| MainClass.Node.Node() | 4.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| MainClass.Node.setDeri(Derivation) | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| MainClass.parseFactor(String,Node) | 38.0 | 0.0 | 7.0 | 1.0 | 9.0 | 1.0 | 8.0 | 8.0 |
| MainClass.parseStr(String) | 33.0 | 2.0 | 12.0 | 2.0 | 35.0 | 6.0 | 9.0 | 13.0 |
| Multi.derivation() | 6.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Multi.Multi() | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Multi.Multi(Derivation,Derivation) | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Multi.print() | 16.0 | 0.0 | 6.0 | 0.0 | 8.0 | 7.0 | 3.0 | 9.0 |
| Operation.getLchild() | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Operation.getRchild() | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Operation.Operation() | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Operation.Operation(Derivation,Derivation) | 4.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Operation.setLchild(Derivation) | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Operation.setRchild(Derivation) | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Total | 349.0 | 3.0 | 71.0 | 6.0 | 124.0 | 82.0 | 81.0 | 116.0 |
| Average | 10.58 | 0.098 | 2.158 | 0.188 | 3.76 | 2.48 | 2.45 | 3.51 |
- 可以看出各类与print相关的方法基本复杂度都比较高,这主要是因为输出时使用了较多的
if-else语句进行判断。除此之外,buildTree()、parseStr()方法的复杂度也比较高,主要是由于控制语句嵌套层数较多。
类复杂度分析
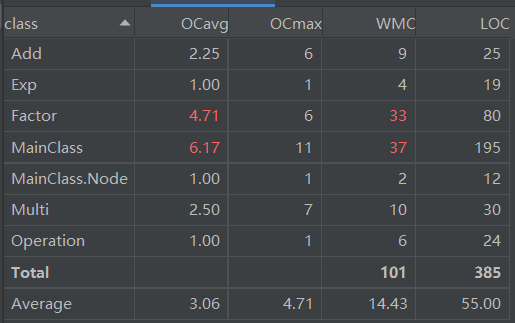
- 可以看出Factor类和MainClass类复杂度较高。
各类代码行数如下:

优缺点分析
优点:相较于第一次作业几乎纯面向过程式的编码,本次作业利用java语言继承、多态等特性,在多个类或子类中实现了同一个求导接口,逐步体现出一些面向对象的思想,增强了代码的可扩展性。虽然这次的架构仍存在一些问题,但总体设计思路以及大部分框架在第三次作业中都可以继续沿用。
缺点:重新阅读第二次作业的代码,我发现有很多冗余的、不合理的设定。
比如我定义了一个父类Operation和继承自该类的两个子类Add和Multi,初衷是希望体现运算符和因子之间的层次关系,并实现代码的复用,但实际上Add类与Multi类的求导及输出方法差异还是比较大的,可复用的代码很有限,定义一个共同的父类并没有多大意义。
其次,我将常数因子、幂函数因子、三角函数因子都定义在一个Factor类中,又定义了一个Exp类用于表示不同类型因子的指数,导致Factor类要实现的功能过于繁重,且增加了不同类之间的耦合度。
此外,由于我一开始认为建树是对输入表达式进行处理的一个环节,因此直接在MainClass类中编写建树代码,导致该类代码行数过多,过于臃肿。为了降低主类的复杂性,应当抽离出一个类专门用于处理输入的表达式并完成建树。
最后,在Derivation()接口中定义一个抽象输出函数print()是不必要的,直接重写每个类的toString()方法即可实现相同功能。
二、测试与bug分析
本次作业在强测和互测中被找出2类bug。
-
在处理表达式最外层括号的时候,我最初采用的策略是直接脱掉,如果中途出现括号不匹配的情况,再交给parseFactor处理。这种方法在遇到括号嵌套情况比较复杂的时候可能会出错。
修复方法:在去掉最外层括号前先判断二者是否匹配,只有匹配时才脱掉括号,而parseFactor()中不再进行括号处理。
-
在Add和Multi类中输出的时候,为了优化多次调用lchild.print()和rchild.print()用于判断,在嵌套层数较多的情况下不停递归调用会消耗很长时间,导致TLE。
修复方法:将同一个函数里用到的lchild.print()和rchild.print()的结果分别保存到变量lresult和rresult中,之后在判断的时候直接使用这两个变量,无需每次都直接调用print()方法。
第三次作业
一、基于度量分析程序结构
UML类图
第三次作业的任务为包含简单幂函数和简单正余弦函数及其嵌套组合函数的导函数的求解,即正余弦函数中也可以包括嵌套因子,除此之外,还要对输入的表达式进行格式判断。我的设计思路是先对输入表达式进行非法空白、非法字符检测,如果不存在这方面的格式错误,就像第二次作业一样开始建树。在建树过程中如果出现正则不匹配的情况,就向上抛出自定义格式错误异常。如果在主函数中捕获到了异常,说明输入格式不合法,直接输出"WRONG FORMAT!",结束程序;否则表明输入格式无误,遂可开始进行链式求导。
UML类图如下:
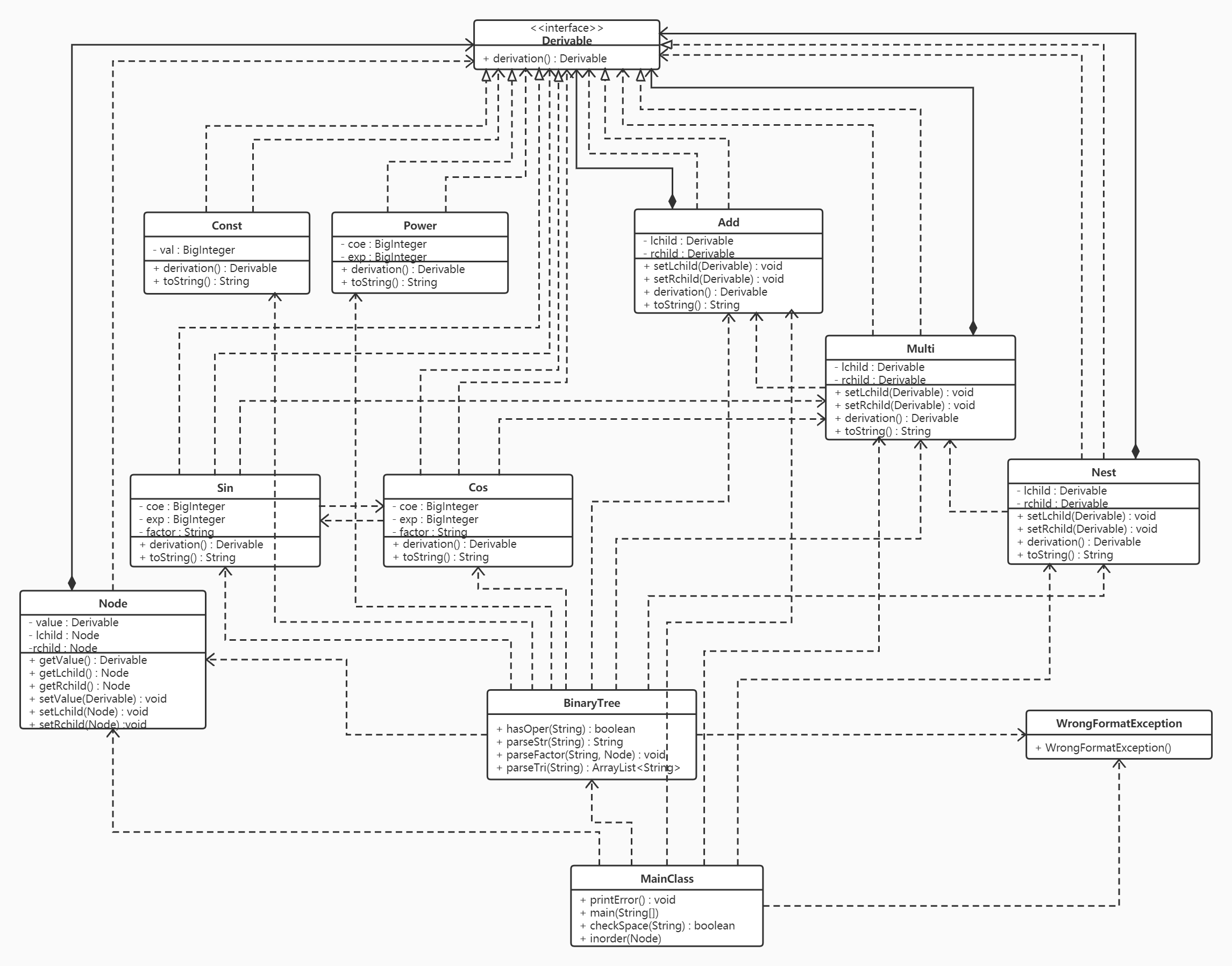
-
求导接口Derivable:
包含抽象求导方法derivation()
-
Const、Power、Sin、Cos分别为常数因子类、幂函数因子类、正弦函数因子类和余弦函数因子类,在这四个类中分别实现求导接口,并重写toString()方法
-
Add、Multi、Nest分别为加法类、乘法类、嵌套组合类,在这四个类中分别实现求导接口,并重写toString()方法
-
Node类为节点类,包含set、get类方法
-
BinaryTree类:
对通过非法空白、非法字符检测的表达式进行解析并将其组织成二叉树结构,如果出现格式不匹配,向上抛出异常
-
主类MainClass:
printError()方法用于输出格式错误信息并结束程序;checkSpace()方法用于检测非法空白和非法字符;inorder()是二叉树中序遍历方法
-
WrongFormatException为自定义格式异常类。
方法复杂度分析
| method | LOC | BRANCH | CONTROL | LOOP | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|---|---|---|---|
| Add.Add() | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Add.Add(Derivable,Derivable) | 4.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Add.derivation() | 4.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Add.setLchild(Derivable) | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Add.setRchild(Derivable) | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Add.toString() | 10.0 | 0.0 | 5.0 | 0.0 | 6.0 | 6.0 | 1.0 | 7.0 |
| BinaryTree.buildTree(String) | 60.0 | 1.0 | 15.0 | 5.0 | 41.0 | 6.0 | 5.0 | 17.0 |
| BinaryTree.hasOper(String) | 8.0 | 0.0 | 1.0 | 0.0 | 3.0 | 2.0 | 4.0 | 5.0 |
| BinaryTree.parseFactor(String,Node) | 36.0 | 0.0 | 7.0 | 1.0 | 16.0 | 5.0 | 9.0 | 9.0 |
| BinaryTree.parseStr(String) | 40.0 | 2.0 | 17.0 | 3.0 | 43.0 | 9.0 | 10.0 | 18.0 |
| BinaryTree.parseTri(String) | 38.0 | 2.0 | 10.0 | 1.0 | 21.0 | 6.0 | 12.0 | 14.0 |
| Const.Const(BigInteger) | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Const.derivation() | 4.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Const.toString() | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Cos.Cos(BigInteger,BigInteger,String) | 5.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Cos.derivation() | 6.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Cos.toString() | 11.0 | 0.0 | 5.0 | 0.0 | 8.0 | 6.0 | 4.0 | 9.0 |
| MainClass.checkSpace(String) | 30.0 | 0.0 | 1.0 | 0.0 | 1.0 | 1.0 | 1.0 | 2.0 |
| MainClass.inorder(Node) | 17.0 | 0.0 | 4.0 | 0.0 | 6.0 | 2.0 | 4.0 | 5.0 |
| MainClass.main(String[]) | 56.0 | 0.0 | 4.0 | 0.0 | 4.0 | 1.0 | 5.0 | 5.0 |
| MainClass.printError() | 4.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Multi.derivation() | 6.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Multi.Multi() | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Multi.Multi(Derivable,Derivable) | 4.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Multi.setLchild(Derivable) | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Multi.setRchild(Derivable) | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Multi.toString() | 11.0 | 0.0 | 6.0 | 0.0 | 8.0 | 7.0 | 2.0 | 9.0 |
| Nest.derivation() | 4.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Nest.Nest() | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Nest.setLchild(Derivable) | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Nest.setRchild(Derivable) | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Nest.toString() | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Node.getLchild() | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Node.getRchild() | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Node.getValue() | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Node.Node() | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Node.Node(Derivable) | 5.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Node.setLchild(Node) | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Node.setRchild(Node) | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Node.setValue(Derivable) | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Power.derivation() | 4.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Power.Power(BigInteger,BigInteger) | 4.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Power.toString() | 11.0 | 0.0 | 5.0 | 0.0 | 8.0 | 6.0 | 4.0 | 9.0 |
| Sin.derivation() | 6.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Sin.Sin(BigInteger,BigInteger,String) | 5.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Sin.toString() | 11.0 | 0.0 | 5.0 | 0.0 | 8.0 | 6.0 | 4.0 | 9.0 |
| WrongFormatException.WrongFormatException() | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 |
| Total | 454.0 | 5.0 | 85.0 | 10.0 | 173.0 | 97.0 | 99.0 | 152.0 |
| Average | 9.66 | 0.11 | 1.81 | 0.21 | 3.68 | 2.06 | 2.11 | 3.23 |
由于本次作业基本上沿用了第二次作业的结构框架,所以出现了类似的问题,即字符串处理、因子解析、建树以及各类的toString()方法的复杂度较高。
类复杂度分析
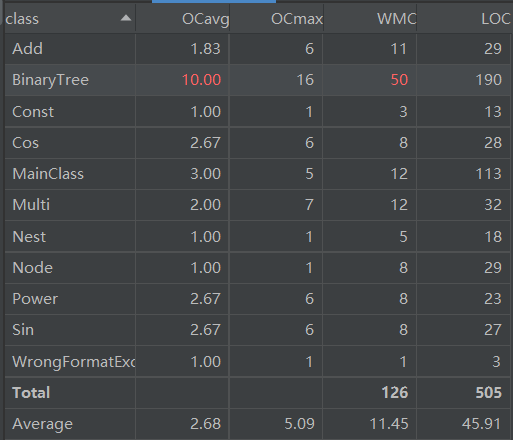
- 可以看出BinaryTree类的复杂度较高。
各类代码行数如下:
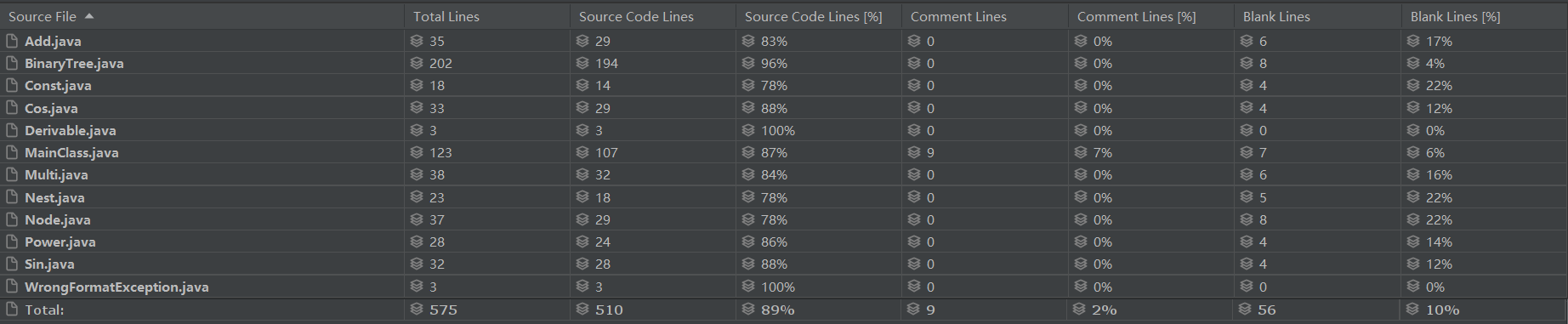
优缺点分析
优点:正确性比较高;去掉了第二次作业中冗余的类和方法,一定程度上降低了类之间的耦合度;具备一定的可扩展性。
缺点:首先,虽然本次作业将表达式解析与建树方法从主类中抽离出来,但由于增添了格式不匹配时的相应处理,导致复杂性仍比较高,应当进一步思考如何优化建树过程。其次,在后两次作业中,我都为幂函数和三角函数设计了系数coe这一属性,但这个设定不够严谨,比如幂函数求导后返回的应当是一个常数因子与幂函数的乘法类,而不是一个修改了系数和指数的幂函数类。
二、测试与bug分析
本次作业在强测和互测中未被测出bug,但由于我仅实现了最基础的结果化简(如去掉含有常数因子0的(乘法)项、化简含有常数因子1的乘法项、去掉最外层多余括号等),故性能分有所损失。
测试策略
- 根据题目中的表述手动构造测试样例,覆盖尽可能多的情况,一方面要考虑多种类型因子的组合和嵌套,另一方面要进行边界测试和压力测试,看看对于长度很长或者或嵌套层数比较多的表达式,会不会出现爆栈以及TLE的情况。
- 参考讨论区同学们的思路,我使用python的xeger模块根据正则自动生成表达式,并用
sympy.diff()对生成的表达式求导,然后将自己或同学的求导结果用与之相减并用sympy.simplify()化简,观察结果是否为0。 - 在第一次互测中,我主要是通过阅读其他同学的代码来发现漏洞。在第二、三次互测中,由于代码规模比较大且大家实现的思路不同,我放弃了直接阅读代码,主要是利用自己翻车的测试点以及一些边界数据hack互测屋内的同学,但此方法缺乏针对性,尤其是在第三次互测中,由于不允许输入非法数据且长度有限制,总体效果不是很好。
重构经历总结
由于第一次作业总体上比较面向过程,能够实现的功能很有限,可扩展性较差,无法满足嵌套需求,因此在第二次作业时我进行了重构。根据之前统计的数据,重构之前各方法的认知复杂度、基本复杂度、设计复杂度、圈复杂度的平均值分别为4.70、1.80、2.90、3.60,重构之后则变为为3.76、2.48、2.45、3.51。可以看出,除了基本复杂度之外,其他复杂度都有所下降,而基本复杂度的上升,主要是因为在print()方法中使用了过多if-else语句所致。总的来说,经过这次重构,程序的结构更加清晰,类之间的耦合度有所下降,并且可以沿用至第三次作业,可扩展性得到了增强。
心得体会
-
使用面向对象语言编程 \(\neq\) 面向对象设计与构造。在上这门课之前,我一直以为所谓的“面向对象”/“面向过程”就是不同编程语言的语言特性,C语言就是面向过程的,python和java就是面向对象的。通过这一个月以来的学习,我逐渐开始理解老师所说的“OO是一种设计思路,与使用哪种语言编程无关”。以我的第一次作业为例,仅管是用java语言编写的,但实现思路中残留着大量面向过程的影子,只是针对当下的需求寻找解决方法,没有考虑如何设计才能满足未来更多可能的需求。在后两次作业,我才逐渐找到了一些面向对象的感觉。所以不管是“面向过程”还是“面向对象”,都是一种思维方式、一种思考问题的方式,和具体的语言没有关系。
-
一个程序的架构直接影响了整个任务实现的流畅性以及出现bug的概率,要满足千变万化的需求,就必须要求有良好的架构。在完成第二、三次作业的过程中,如果我硬着头皮在最初的架构上反复修改,即使最终能实现相应的功能,方法的复杂度也一定会很高。所以如果发现当前框架的可扩展性比较差,就要及时止损,尽早进行重构,避免给日后带来更大的工作难度和工作量。但同时,我认为好的架构往往都是通过反复迭代修改演变而来的,不是一蹴而就设计出来的。我相信在这三周内没有进行重构的同学只是极少数,大部分同学还是像我一样,随着任务难度的增加逐渐发现先前架构中不合理的地方。为了减少不必要的重构,我们应当在开始编码之前思考一下未来潜在的需求,尽量提高程序的可扩展性。
-
大量、充足的测试是保证程序质量的重要手段。由于课程组提供的中测强度很低,如果不想在强测和互测中被找出一堆bug,就要自己进行大量有效的测试,一方面可以借助自动化测试手段进行批量测试,另一方面也要考虑边界和异常数据。
-
不畏难、精益求精才能做得更好。在研讨课上,我发现很多同学都对输出结果进行了优化,包括但不限于因式分解、展开括号、利用三角函数性质化简等手段。相比之下,出于减轻工作量和确保正确性考虑,我只实现了最基础的化简。抛开成绩不谈,无论最终是否能达到预期效果,我们都应该尽最大的努力做到更好,不能因畏难和害怕出错就放弃提升的机会。
OO第一单元到此结束了,我与多项式求导的爱恨情仇也暂时告一段落了。希望接下来我能够继续努力,继续进步,真正体会到OO的强大之处。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号