蓝桥杯-数字拆分

题目描述

 

 

 

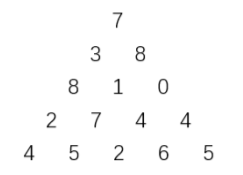
上图给出了一个数字三角形。从三角形的顶部到底部有很多条不同的路径。对于每条路径，把路径上面的数加起来可以得到一个和，你的任务就是找到最大的和。

路径上的每一步只能从一个数走到下一层和它最近的左边的那个数或者右 边的那个数。此外，向左下走的次数与向右下走的次数相差不能超过 1。

输入描述

输入的第一行包含一个整数 N (1≤N≤100)，表示三角形的行数。

下面的 N 行给出数字三角形。数字三角形上的数都是 0 至 100 之间的整数。

输出描述

输出一个整数，表示答案。

 

思路

这里和普通的dp只多了一个限制，就是向左下走的次数与向右下走的次数相差不能超过 1。而加了这个限制的话，就代表我们最后走到的位置是固定的，如何n为奇数，走到的位置一定是(n,n/2+1),如果n为偶数，走到的位置为(n,n/2)或者(n,n/2+1)，所以，只需要先走一遍dp，找出所有的最大路径，然后输出我们走到的位置的最大路径即可

dp步骤

1.确定dp数组的含义，这里我们使用二维数组dp[i][j]，dp数组的含义是存储前i行，前j列的路径，dp[i][j]存储的是从起点到(i,j)的最大路径

2.确定状态转移方程，dp[i][j]可以由两个值得来，一个是dp[i-1][j-1],一个dp[i-1][j],取这两者的最大值，再加上a[i][j]，于是得到状态转移方程为

dp[i][j] = max(dp[i-1][j-1],dp[i-1][j]) +a[i][j]

3.确定结果，如果n为奇数，最大值为dp[n][n/2+1],如果n为偶数，则最大值为max(dp[n][n/2],dp[n][n/2+1])

代码

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int dp[N][N];
int a[N][N];
int n;
int main()
{
  cin >> n;
  for(int i = 1;i <= n;i++)
  {
    for(int j = 1;j <= i;j++)
    {
      cin >> a[i][j];
    }
  }
  for(int i = 1;i <= n;i++)
  {
    for(int j = 1;j <= i;j++)
    {
      dp[i][j] = max(dp[i-1][j-1],dp[i-1][j]) + a[i][j];
    }
  }
  if (n%2 == 0)
  {
    cout << max(dp[n][n/2],dp[n][n/2+1]);
  }
  else
  {
    cout << dp[n][n/2+1];
  }
  return 0;
}